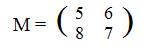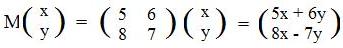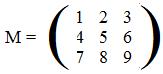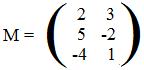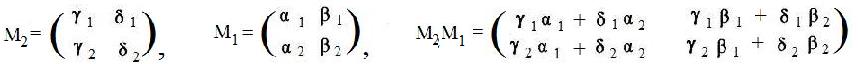Return to Chapter 5
Additional Material for Chapter 5
A product of linear transformations is a linear transformation
Needed to show are the two conditions:
(a) L2L1(p + q) = L2L1(p) + L2L1(q), (homomorphism)
(b) L2L1(λp) = λ L2L1(p), (homogeneous),
where p and q are any (position) vectors in the plane and λ is any real number.
L2L1 satisfies (a):
L2L1(p + q) = L2(L1(p) + L1(q)) = L2L1(p) + L2L1(q)
(That L1 is a homomorphism justifies the first equality, and that L2 is a homomorphism justifies the second equality.)
L2L1 satisfies (b):
L2L1(λp) = L2(λ L1(p)) = λ L2L1(p)
(That L1 is homogeneous justifies the first equality, and that L2 is homogeneous justifies the second equality.)
Chain of Equalities for F(x,y) = (2x,3y) to be a Linear Transformation
F(p + q) = F((x1,y1) + (x2,y2)) = F(x1+x2, y1+y2) =
(2(x1+x2), 3(y1+y2)) =
(2x1,3y1) + (2x2,3y2) =
F(x1, y1) + F(x2, y2) = F(p) + F(q)
Geometric approach to linear transformations
Since these linear universes are sets, there exist functions that carry all the points from a linear universe into a linear universe. These functions will be given some further conditions to become acceptable functions. For example, a function may carry all the points of a line onto a line. It is possible to find a function that carries an entire plane onto a single line. A function that carries a line onto a semi-circle would not be considered acceptable since a semi-circle is not one of the four linear universes. Another condition on acceptable functions is that the origin is carried by them onto the origin. A function that carries an entire linear universe onto a single point (it must be an origin) is called trivial or constant. Such functions are acceptable, but not very interesting.
One of the geometric figures that receives much attention in these discussions is the parallelogram. Only functions that preserve the form of a parallelogram will be acceptable. This means that if points O,P,R,Q are vertices of a parallelogram, then images O,F(P),F(R),F(Q) must also be vertices of a parallelogram. (See adjacent Fig1.) A slight problem occurs if F carries all of the points in the first linear universe onto points of some line. Then the four images are points of a "collapsed parallelogram".
(See adjacent Fig2.). Click here to see a discussion of collapsed parallelograms.
The opposite sides of a parallelogram are parallel. This forces acceptable non-trivial functions to carry parallel lines onto parallel lines. (Assume that any line is parallel to itself.) Such functions are said to "preserve parallelism." There are functions in a higher geometry, called projective geometry, that carry lines onto lines but do not preserve parallelism.
There is another condition that "acceptable functions" must satisfy. Given any two parallel line segments. They may or not be congruent. However, a quotient of their lengths forms a ratio. An acceptable function will carry these parallel segments onto parallel segments preserving the ratio of their lengths. Therefore, if A and B are the end points of the first segment, and C and D are the end points of the second segment, then F(A) and F(B) are the end points of the image of the first segment, and F(C) and F(D) are the end points of the image of the second segment. Then if λ = length AB/lengthCD then also λ = length F(A) F(B)/length F(C) F(D) if F(C) and F(D) are distinct.
It should be emphasized that an acceptable function need not preserve lengths, only the ratio of lengths. It can carry a trapezoid onto a much larger or much smaller trapezoid, but the ratio of lengths of the parallel sides of each trapezoid must be the same. The ratio condition exists only if the segments are parallel. Parallel segments become congruent if the ratio of their lengths = 1.
[2.1] (Acceptable functions) A function is acceptable if it satisfies all of the following conditions:
(a) It carries all of the points of some linear universe onto a linear universe;
(b) It carries the orgin of the first linear universe onto the origin of the second linear universe;
(c) If two line segments are parallel, then it carries them onto parallel line segments, providing they are not points. Furthermore, the ratio of the lengths of the segments in the first linear universe equals the ratio of the lengths of the segments in the second linear universe.
(d) It carries the four vertices of a parallelogram in the first linear universe onto the four vertices of a parallelogram in the second linear universe.
The acceptable functions belong to "linear geometry". If condition (b) is removed, then the functions only belong to "affine geometry."
Some of these conditions are redundant. It is possible to prove (d) from (c).
The use of position vectors makes the discussion shorter and, hopefully, more understandable. Since linear universes contain an origin O, position vectors exist and any point may be located by a position vector: p = OP locates point P in some linear universe. Let F be a function from that linear universe onto a linear universe. Then F carries point P onto some point F(P) in the second linear universe and therefore F(p) = F(OP) = F(O)F(P) = OF(P) is a position vector from O to point F(P) and locates point F(P) in the second linear universe. It will be convenient in discussions to switch between points and their position vectors that locate the points. Therefore, F carries points onto points as well as their position vectors onto position vectors.
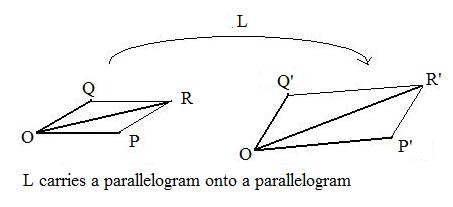The sum of two position vectors p and q can be done in geometry using a parallelogram. The points Q, O, P are three adjacent vertices of the parallelogram. The fourth point S is located by the position vector OS which is a diagonal of the parallelogram. If F is an acceptable function then F carries the origin onto the origin and parallelograms onto parallelograms. Therefore, points F(Q),O,F(P) are three of the vertices of a parallelogram. The fourth point is is located by a position vector obtained by addition of vectors F(p) and F(q). But the acceptable function carries parallelogram onto parallelogram and therefore carries point S onto this fourth point. Therefore,
F(p) + F(q) = OF(S) = F(OS) = F(p + q)
for any position vectors p and q in the first linear universe
Therefore,
(*) F(p + q) = F(p) + F(q)
This makes F an additive homomorphism. All additive homorphisms carry 0 onto 0. To show this, since 0 = 0 + 0, F(0) = F(0 + 0) = F(0) + F(0). Then subtract F(0) from the equation just found, F(0) = F(0) + F(0) to get 0 = F(0).
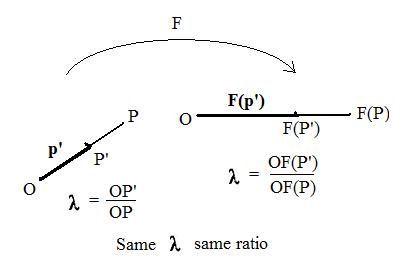Let P' be any point on the line through distinct points O and P. Suppose O is not between P' and P as shown in the adjacent figure. This makes the ratio λ = OP'/OP non-negative. An acceptable function F carries these collinear points onto collinear points O, F(P') and F(P). Because F preserves ratios of lengths of line segments, λ = OF(P')/OF(P). Therefore for both figures,
OP' = λOP and OF(P') = λOF(P)
In the language of position vectors this translates into
p' = λp and F(p') = λF(p)
Replace p' in this last equation by λp to get
(*) Fλp) = λF(p)
But the discussion has supported this equality only for λ>0. (It is trivially true for λ=0.) Some simple manipulations will show that the equation is true for λ<0 without direct geometric support.
Since F is a homomorphism,
F(λp + (-λ)p) = F(λp) + F((-λ)p)
Therefore,
0 = F(0) = F(λp) + F((-λ)p)
This means that
F(λp) = - F((-λ)p)
But - λ >0 , so from the argument above, F((-λ)p) = (-λ)F(p). Therefore,
F(λp) = -(-λ)F(p)
or
(**) F(λp) = λF(p)
Equations (*) and (**) become necessary conditions that a function F be a linear transformation: F = L.
Linear Expressions Relate Matrices and Corresponding Functions
It is simple to find values for the linear expressions
(*) 5x + 6y and 8x - 7y
if numerical values are given to x and y. If x and y are given values 3 and 4 respectively, then the expressions become
5(3) + 6(4) = 39 and 8(3) - 7(4) = - 4
By giving other values to x and y simultaneously, the two expressions have numerical values. Form the horizontal arrays (3,4)'and (39,-4) . To the first array the linear expressions associate the second array. This action can be written
(3,4) --> (39,-4)
The expressions can also be applied to vertical arrays:
(3,4)' --> (39,-4)
The reader can easily verify:
(1,-1)' --> (-1,15)', (4,1)' --> (26,25)', (α,β)' --> (5α + 6β, 8α - 7β)'
Consider these arrays as locating points in a plane. For each point (x,y)' in the plane the expressions assign a unique point (5x+6y,8x-7y)'. But this action satisfies the definition of a function, carrying points in a plane onto points in the same plane:
(**) L(x,y) = (5x+6y,8x-7y)
Here,
L(3,4) = (39,-4), L(1,-1) = (-1,15), L(4,1) = (26,25)
It is convenient to use the same function L for vertical arrays:
L(3,4)' = (39,-4)', L(1,-1)' = (-1,15)', L(4,1)' = (26,25)'
Using the coefficients of the linear expressions (*), form a 2x2 matrix:
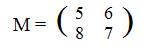Thinking of M (x,y)' as a matrix product of a 2x2 and a 2x1 matrices:
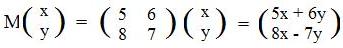Compare this equation involving matrices with the definition (**) of function L, intuitively speaking, M and L do the same thing to points in the plane. More exactly, M and L perform the same action on the coordinates of every point in the plane. The only difference is that by notation L involes horizontal arrays, but M involves vertical arrays.
There is a similar discussion for 3x3 matrices and points in space. Given the linear expressions,
x + 2y + 3z, 4x + 5y + 6z, 7x + 8y + 9z
the function L can be formed: L(x,y,z) = (x+2y+3z, 4x+5y+6z, 7x+8y+9z) and the matrix M that corresponds to L is:
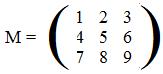The reader can verify that the product M(x,y,z)' = (x+2y+3z, 4x+5y+6z, 7x+8y+9z)'.
The linear expressions
2x + 3y 5x - 2y -4x + y
receive values for x and y and return values for the three expressions. Therefore, they carry points from a plane into space:
(x,y)' --> (2x+3y, 5x-2y, -4x+y)'
The function for this action is L defined by L(x,y) = (2x+3y, 5x-2y, -4x+y). The matrix is
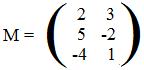For example, Let M act on point (6,7)' and let L act on the same point (6,7):
M(6,7)' = (2(6)+3(7), 5(6)-2(7), -4(6)+1(7))' = (33, 14, -17)'
L(6,7) = (33, 14, -17).
By the matrix product a non-square matrix "changes" a column array of some length into a column array of a different length. The corresponding function carries an array of some length onto an array of a different length. Intuitively speaking, they both carry points in some dimension onto points in another dimension.
Products of associated matrices are associated with products of linear transformations
The discussion involves only the plane as the linear universe. For other linear universes, the discussions are similar.
Given: Two linear transformations L1 and L2 from the plane into the plane with associated matrices M1 and M2 respectively.
To show that the product M2M1 of the matrices is the associated matrix of the product (composition) L2L1. L2 and L1 carry the special arrays (1,0) and (0,1) onto arrays of length two, say
L2(1,0) = (γ1, γ2), L2(0,1) = (δ1, δ2),
L1(1,0) = (α1, α2), L1(0,1) = (β1, β2)
The images of the special arrays become vertical columns in the associated matrices M2 and M1:
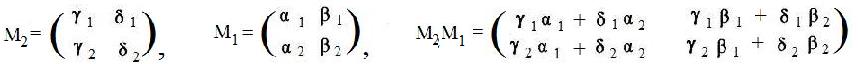Now
L2L1(1,0) = L2(α1, α2)
= L2(α1(1,0) + α2(0,1))
= α1L2(1,0) + α2L2(0,1)
= α1(γ1, γ2) + α2(δ1, δ2)
= (α1γ1 + α2δ1, α1γ2 + α2δ1)
= first column of M2M1
Similarly,
L2L1(0,1) = L2(β1, β2)
= ...
= ...
= ...
= (β1γ1 + β2δ1,
β1γ2 + β2δ2)
= second column of M2M1
This makes M2M1 the matrix associated with L2L1.
Distrance preserving means linear transformation
Two lemmas are proven and then used in the main theorem.
Lemma 1 A function F on the planesp3 that preserves distance also preserves betweenness.
Notation: if point B is on a line segment between end points A and C, then image F(B) is on the line segment between images F(A) and F(C) that are the end points.
Given a point B on the line segment AC. Then distances
|AB] + |BC| = |AC|
Also given that function F preserves distance. Let A',B',C' denote the images of A,B,C. Then because F preserves distance,
|AB| = |A'B'|, |BC| = |B'C'| |AC| = |A'C'|
Substituting these into the first equation produces
|A'B'| + |B'C'| = |A'C'|
This last equality means that point B' is on the line segment A'C', that is, between end points A' and C'.
Lemma 2 A function F on the planesp3 that preserves distance also preserves collinearity.
Notation: if points P,Q,R are collinear, then images P',Q',R' are collinear.
There are three ways that P,Q,R can be collinear:
Q,P,R where P is between Q and R, P,Q,R where Q is between P amd R, P,R,Q where R is between P and Q
Then respectively, P' is between Q' and R', Q' is between P' and R', R' is between P' and Q'
But in each situation, points P',Q',R' are collinear.
(Distrance preserving means linear transformation) Any function on the planesp3 that preserves distance and leaves the origin fixed is a linear transformation.
Let P and Q be any points such that O,P,Q are not collinear. Then position vectors p and q locate the points P and Q. Let R be the point located by r = p + q. Then O,P,R,Q are vertices of the addition parallelogram. For any function F preserving distance and leaving the origin fixed, let O,P',R',Q' be their images. Then these points are vertices of a parallelogram congruent to the parallelogram O,P,R,Q. Hence r' = p' + q'. Therefore,
F(p + q) = F(r) = F(OR) = OR' = r' = p' + q' + F(p) + F(q)
Thus F preserves addition.
Let F be a function that preserves distance and carries the origin O onto itself. To show that F is homogeneous, that is
F(λp) = λF(p) for any position vector p and any real number λ
Let position vector q = λp. Then points O, Q, P are collinear. Q may or may not be between O and P. Let P' and Q' be the images of P and Q. Then norms |OP'| = |OP| and |OQ'| = |OQ|.
Case I: Q is between O and P. Then q points in the same direction as p and λ must be positive.
By Lemma 1, images Q' is between O and P'. Now
|OQ'|/|OP'| = |OQ|/|OP| = λ
Then |OQ'| = λ|OP'|. But since λ is positive, OQ' = λOP'. This means that
F(λp) = F(q) = q' = λp' = λF(p)
Therefore, F is homogeneous if λ is positive.
Case II: O is betweem Q and P.
The linear transformation that interchanges coordinates preserves distance.
Let L be the linear transformation that interchanges coordinates: L(x,y) = (y,x).
Let P and Q be any points. Their images are
P' = L(P) and Q'=L(Q)
Since P and Q are points on the coordinate plane they have coordinates:
P(α,β) and Q(γ,δ)
Then their images have (switched) coordinates
P'(β,α) and Q'(δ,γ)
Using squares of the norms,
(distance between P' and Q')2 = |P'Q'|2 = |q' - p'|2 = |(δ,γ) -
(β, α)|2 = |(δ - β, γ - α)|2 = (δ - β)
2 + (γ - α)2
(distance between P and Q)2 = |PQ|2 = |q - p|2 = |
(γ,δ) - (α,β)|2 = |(γ - α, δ - β)|2 =
(γ - α)2 + (δ - β)2
Since (δ - β)2 + (γ - α)2 = (γ - α)2
+ (δ - β)2 then distance between P' and Q' = distance between P and Q.
Given below under reflections about lines is a simple geometric interpretation for L in this example.