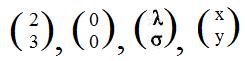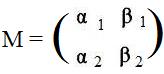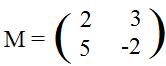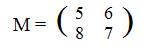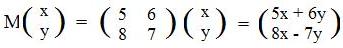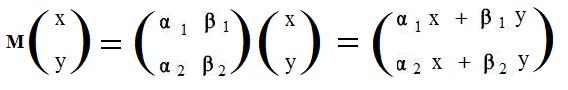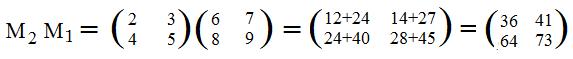Go to other chapters or to other branches of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer programs
sp3
sp3
Chapter 5
Linear Transformations
Recall that a universe is the superset in which all elements and subsets under discussion are located. In the following discussions any one or more of four geometric universes are involved at any time: point, line, plane and space. They have dimensions 0,1,2 and 3 respectively. They become linear universes if they contain a distinguished point called the origin, which is denoted by O. The universe of just the origin is seldom of interest, and may be called the trivial universe. More interesting are the plane and space, and in many discussions below, the universe will be the two-dimensional plane.
However, many discussions involving the plane can be extended with obvious or slight modifications to discussions involving 3-dimentional space. For example, in some situations simply replace the word "plane" with "space". A small symbol sp3 after a key word or before a paragraph indictes this extension. Sometimes there is a blue symbol sp3 with an underline. The reader may click on ths link to see pertinent or additional information involving 3-dimensional space. Discussions involving geometric universes of dimensions greater than 3 exist but are beyond the scope of this chapter.
Throughout this chapter the letter L will denote a linear transformation. Also used are L' and L with subscripts L1, L2, ..., when more than one linear transformation are being discussed.
Section 1: The 3 properties that together define a linear transformation
A functionsp3 on the plane carries all points in that plane onto (image) points in that plane. (However, not all points need be images, but they may be.) Since the plane has an origin, position vectors exist, locating all points. The first property of a linear transformation is given in the following:
[1.1a] A linear transformationis is a function that carries points onto points in such a way that all position vectors are carried onto position vectors.
Notation: If p is a position vector, then its image L(p) is also a position vector.
It will be often be convenient to denote images L(P), L(Q), L(R) of points P, Q, R by P', Q', R'. Similarly, the images L(p), L(q), L(r) of position vectors p, q, r may be denoted by position vectors p', q', r'. The above notation may read:
Notation: If p is a position vector, then its image p' is also a position vector, where p' = L(p).
The statement [1.1a] gives the correct impression that the primary purpose of linear transformations involve actions on position vectors. Those actions are done by carrying points in a special way. It is not difficult to discover that way because the initial point (tail) of every position vector is the origin. The following is equivalent to [1.1a]
[1.1b] Every linear transformation is a function that leaves the origin fixed. It always carries the origin back onto itself.
The remaining and last of the defining properties of linear transformations concern their actions on sums of position vectors and products of a real numbers and a position vectors.
Given two position vectors p and q their images are p' = L(p) and q' = L(q). The pairs of position vectors can be added to form two sums:
p + q and p' + q'
Is there any relationship between the two sums?
[1.2a] (Preserving sums) A linear transformation carries the sum of any two position vectors onto the sum of the images of those position vectors.
Notation: L(p + q) = p' + q'.
Notation: L(p + q) = L(p) + L(q).
Actually, the word "two" may be omitted. Image of a sum equals the sum of the images.
[1.2b] (Preserving sums) A linear transformation carries the sum of any number of position vectors onto the sum of all the images of those position vectors.
Notation: L(p + q + r + ...) = p' + q' + r' + ....
Notation: L(p + q + r + ...) = L(p) + L(q) + L(r) + ...
Click here to see a proof by induction that [1.2a] implies [1.2b].
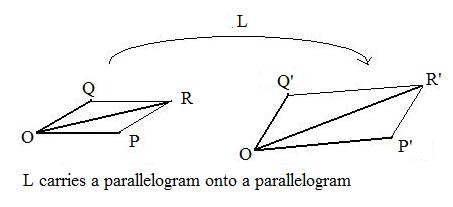 Let r = p + q. Then points O,P,R,Q are vertices of a parallelogram (the parallelogram of addition of vectors). Now L carries position vectors p,q,r onto position vectors p',q',r' and by [1.2a] r' = p' + q'. Therefore points O,P',R',Q'' are vertices of a parallelogram. Therefore, L carries the vertices of parallelogram OPRQ onto the vertices of parallelogram OP'R'Q'. Later, it will be shown that every linear transformation carries segments onto segments. Hence, every linear transformation carries parallelograms with one vertex on the origin onto parallelograms with one vertex on the origin.
Let r = p + q. Then points O,P,R,Q are vertices of a parallelogram (the parallelogram of addition of vectors). Now L carries position vectors p,q,r onto position vectors p',q',r' and by [1.2a] r' = p' + q'. Therefore points O,P',R',Q'' are vertices of a parallelogram. Therefore, L carries the vertices of parallelogram OPRQ onto the vertices of parallelogram OP'R'Q'. Later, it will be shown that every linear transformation carries segments onto segments. Hence, every linear transformation carries parallelograms with one vertex on the origin onto parallelograms with one vertex on the origin.
It is possible to add a vector to itself many times. This produces integer coefficients. A linear transformation L carries that product of coefficient and vector onto a product of that coefficient and the image of the vector, as shown here:
L(2p) = L(p + p) = L(p) + L(p) = 2L(p);
L(3p) = L(p + p + p) = L(p) + L(p) + L(p) = 3L(p);
...............................................................................................................................................................
L(np) = L(p + p + p + ... + p) = L(p) + L(p) + L(p) + ... + L(p) = nL(p);
This motivates the following:
[1.3] (Preserving coefficients) Every linear transformation carries the product of a real number and a position vector onto the product of that same real number and the image of the position vector.
Notation: L(λp) = λL(p);
Notation: L(λp) = λp'
The statements [1.1], [1.2], [1.3] together define a linear transformation. They are summarized [2.1].
By taking λ = 1/2 every linear transformation carries midpoints onto mid points. But the diagonals of a parallelogram bisect each other. A linear transformation carries the diagonals onto diagonals that bisect each other. This makes the miage of a parallelogram also a parallelogram. The parallelograms can be anywhere, and need not have any vertices at the origin.
[1.4] (Preserving parallelograms) A linear transformation carries parallelograms onto parallelograms.
The parallelograms need not be congruent or even similar. But [1.4] implies that a linear transformation carries parallel lines onto parallel lines. That in turn implies that a linear transformation carries parallel segments onto parallel segments. The ratio of their lengths is preserved. Finally, a linear transformation carries trapezoids onto trapezoids. Again the trapezoids may appear to be very different but still can be recognized as trapezoids.
Section 2: The basic algebra of linear transformations
[2.1] (Definition of a linear transformation)sp3 A function L on a plane that carries all position vectors onto position vectors is a linear transformation if and only if it satisfies the following two conditions where p and q are any position vectors in the plane and λ is any real number.:
(a) it carries the sum of position vectors onto the sum of their images; (homomorphism)
Notation: L(p + q) = L(p) + L(q)
(b) it carries the product of any real number and any position victor onto the product of that same real number and the image of the position vector (homogeneous),
Notation: L(λp) = λL(p)
It is easy to show that a linear transformation leaves the origin fixed. Simply set λ in (b) to zero and get
L(0) = 0.
It is also easy to prove that L preserves subtraction:
L(p - q) = L(p + (-q)) = L(p) + L(-q) = L(p) - L(q)
So the image of p - q is p' - q'.
An immediate result of this fact is that a linear transformation carries all vectors (not just position vectors) onto vectors: it carries vector AB onto vector A'B', because it carries the linear combination b - a onto b' - a'.
Recall the discussions about linear combinations of position vectors in Chapter 4 of this volume. The following important statement is a useful equivalent to definition [2.1].
[2.2] (Preserving linear combinations) A function is a linear transformation if and only if it carries every linear combination of position vectors onto a linear combination with the same coefficients of the corresponding images of the position vectors.
Notation: L(αa + βb + γc + ...) = αa' + βb' + γc' + ...
Notation: L(αa + βb + γc + ...) = αL(a) + βL(b) + γL(c) + ...
Click here to see a discussion supporting this statement.
In the following examples, suppose a linear transformation carries distinct points onto distinct points.
Example 1:sp3
In the chapter on vectors the centroid G of a triangle ABC was located by the position vector g which satisfied
3g = a + b + c
This is an equality between two linear combinations of position vectors. Therefore, any linear transformation acting on both sides produces the equation
3g' = a' + b' + c'
This says that every linear transformation carries the centroid G of a triangle onto the centroid G' of the image of the triangle.
Example 2:
Suppose point P is on a line through distinct points A and B. Then there is a real number λ satisfying the vector equation:
AP = λAB
This is equivalent to the equation involving position vectors and coefficients:
p = (1 - λ)a + λb
Apply any linear transformation to both sides of the equality to get:
p' = (1 - λ)a' + λb'
This is equivalent to the equation:
A'P' = λA'B'
Then the image P' is on the line through A' and B'. This means that the linear transformation carries the line AB into line A'B'. But λ can be any real number, so that the linear transformation carries points onto all of line A'B'. This says that linear transformations carry lines onto lines.
It also says that they carry segments onto segments. Merely restrict λ to values between 0 and 1 inclusive.
.
It is trivial to show that the identity function I satisfies all the conditions of a linear transformation.
Recall the product (composition) of functions. Using it, it is possible to combine linear transformations.
[2.3] (Products of linear transformations) The product of two linear transformations on the plane is a linear transformation on the plane.
Notation: If L1 and L2 are linear transformations on the plane then L2L1 is a linear transformation on that plane.
Click here to see the discussion supporting this statement.
Consider now a linear transformation L and a linear transformation L' on the same planesp3. If it happens that their product is the identity I
LL' = I L'L = Ithen L' is called the inverse of L.
The inverse of L is written L-1.
For example, if L is defined by L(p) = 2p then L-1 is defined by L-1(p) = (1/2)p.
Not every linear transformation has an inverse. If a linear transformation has no inverse, then that transformation is called singular. If it has an inverse then it is non-singular. The geometric interpretation of a singular linear transformation will be later as a linear transformation that carries some line onto a point.
[2.4] (Groups of linear transformations) The collection of all non-singular linear transformations carrying a planesp3 onto itself forms a group.
Recall that a necessary condition that a function have an inverse is that it be one-to-one (1-1). That means that the function carries distinct points onto distinct points. In symbols, if point P is different from point Q then point F(P) is different from point F(Q). The contrapositive to this says F(P) = F(Q) implies P = Q.
Suppose that a linear transformation L is one-to-one. This means that only the origin is carried onto the origin: L(O) = O and for any point P different from the origin L(P) cannot be the origin. The following statement guarantees the truth of the converse. Intuitively speaking, if L is one-to-one at the origin, then L is one-to-one everywhere.
[2.5] (Condition for a linear transformation to be one-to-one) A linear transformation is one-to-one if and only if the only point carried by it onto the origin is the origin itself.
Notation: O is the only point carried onto the origin [L(P) = O implies P = O] is equivalent to saying that L is one-to-one.
Proof for showing if O is the only point carried onto the origin &nbnsp; then L is one-to-one.
Using position vectors, given L(p) = 0 implies p = 0. Let A and B be any points. If they have a common image then L(A) = L(B). Then
L(A) = L(B) ==> L(a) = L(b) ==> L(a) -- L(b) = 0 ==> L(a -- b) = 0 ==> a -- b = 0 ==> a = b ==> A = B
The first and last expressions of this chain of implications guarantee that L is one-to-one. (Note that the hypothesis is used at the red implication (==>)).
[2.6] A one-to-one linear transformation carries any linear independent position vectors onto linear independent position vectors.
Notation: if a,b,c,d are linearly independent position vectors, then L(a), L(b), L(c), L(d) are linearly independent.
To test L(a), L(b), L(c),L(d) for linear independence, form the linear combination and equate it to zero: αL(a) + βL(b) + γL(c) + δL(d) = 0. It is sufficient to show that this implies that all the coefficients are zero.
αL(a) + βL(b) + γL(c) + δL(d) = 0 ==> L(αa) + L(βb) + L(γc) + L(δd) = 0 ==> L(αa + βb) + γc) + δd) = 0
==> αa + βb) + γc) + δd = 0 ==> α = β = γ = δ = 0
The red ==> shows where the hypothesis that a,b,c,d are linearly independent is used. The first and last expressions of this chain of implications show that L(a), L(b), L(c), L(d)
A linear transformation must carry at least one point onto the origin (called the image origin.). It may carry more than one point onto the image origin. The set of all points carried by a linear transformation onto the image origin is called the kernel of the linear transformation. Statement [2.5] implies that if the kernel consists of a single point, then the linear transformation is one-to-one. Intuitively speaking, the kernel measures how far away a linear transformation is from being one-to-one: the bigger the kernel the less one-to-one (the more points anywhere are carried onto the same point). An extreme example: the kernel of the trivial linear transformation, that carries all the points of the planesp3 onto the origin, is the whole plane.
[2.7] The kernel of a linear transformation is a vector space (sub-space).
Notation: If S is the set of all points such that L(S) = O then the position vectors to all points in S form a vector space.
If p and q are in the kernel of a linear transformation L, then
L(p + q) = L(p) +L(q) = 0 + 0 = 0
So their sum p + q is in the kernel.
Let λ be any real number and again let p be in the kernel. Then
L(λp) = λL(p) = λ0 = 0
So λp is in the kernel.
The kernel inherits the remaining characteristics for a vector space from the linear space of which the kernel is a subset.
Section 3: Linear transformations on the coordinate plane
Each point in the coordinate plane has an attached array with a first coordinate and a second coordinate (an x-coordinate and a y-coordinate)sp3. If a linear transformation on the plane carries each point onto a point in the plane, what is the relation between the coordinates of the two points?
Playing a fundamental role in discussions in this section are special pointssp3 (1,0) and (0,1). They are located on the x-axis and the y-axis. Sometimes the points are given names E1 and E2, so that
E1(1,0) E2(0,1)
denote the special points. The position vectors e1 and e2 locating these points are special vectors. These position vectors e1 and e2 in some previous discussions were the orthonormal vectors i,j. But here the arrays (1,0) and (0,1) will denote both the special points and the special position vectors e1 and e2 locating them.
A point (2,3) is equal to a linear combination of the special points (1,0) and (0,1):
(2,3) = 2(1,0) + 3(0,1)
Notice that the coordinates 2 and 3 in (2,3) become coefficients in the linear combination 2(1,0) + 3(0,1).
In fact, any point (x,y) is equal to a linear combination of special points in which x and y become coefficients:
(x,y) = x(1,0) + y(0,1)
because x(1,0) + y(0,1) = (x,0) + (0,y) = (x+0,0+y) = (x,y).
Apply a linear transformation L to both sides of the above equality between two linear combinations:
(*) L(x,y) = xL(1,0) + yL(0,1)
because the linear transformation preserves coefficients, which in this case are x and y. But (*) supports the following statement:
[3.1] (Linear combinations of images of special points)sp3 For any linear transformation on the plane, the image of any point is equal to a linear combination of special points where the coordinates of the given point are coefficients.
Notation: L(x,y) = xL(1,0) + yL(0,1)
There is an important interpretation for the equality in (*):
A linear transformation is completely determined by its images of the special points.
Notation: If L(1,0) and L(0,1) are known, then L(x,y) is known for any point (x,y) because of (*) above.
Example:
if L(1,0) = (6.7) and L(0,1) = (4,5) then L(x,y) = x(6,7) + y(4,5) = (6x + 4y, 7x + 5y)
Expressions like 6x + 4y and 7x + 5y occur frequently in these discussions. A name is given to them.
A linear expressionsp3 in x and y is a an expression αx + βy, where α and β are any real numbers, called coefficients.
Examples:
(**) 2x + 3y, 5x - 2y, -4x + y
are linear expressions in x and y. The numbers 2, 3, 5, -2, -4, 1 are the coefficients.
Using zeros as coefficients, the three expressions x, y, 0 are linear expressions because they are equal to 1x + 0y, 0x + 1y, 0x + 0y respectively.
Linear expressions are similar to linear combinations, but the latter involve position vectors, and linear expressions contain no vectors, only x and y with numbers. The letters x and y may be replaced by numbers. Then the expressions have numerical values. For example, if x and y are replaced by -2 and 1 respectively, the the above three expressions (**) have the values -1, -12, 9 respectively. Notice that if x and y are replaced by zeros then any linear expression has the value of zero. For this reason, linear expressions may be called homogeneous.
[3.2] (Linear transformations and coordinates) sp3 A linear transformation carries the arbitrary point (x,y) onto a point, that has two coordinates which are linear expressions in x and y.
Notation: L(x,y) = (α1x + β1y, α2x + β2y)
In discussions in this chapter the equation
L(x,y) = (α1x + β1y, α2x + β2y)sp3
is called the formula for the linear transformation L on the coordinate plane.
The argument supporting [3.1] uses special points. In the plane they are (1,0) and (0,1). Their position vectors in previous discussions were the orthonormal vectors i,j ). respectively.)
The argument here supports (a). Similar arguments support (b),(c),(d).
Use is made of the fact that (x,y) can be expressed as a linear combination: (x,y) = x(1,0) + y(0,1) A linear transformation L must carry the special points onto points in the plane, say
L(1,0) = (α1, α2) and L(0,1) = (β1, β2)
Therefore,
L(x,y) = L(x(1,0) + y(0,1)) = L(x(1,0)) + L(y(0,1)) = xL(1,0) + yL(0,1) = x(α1, α2) + y(β1, β2) = (α1x + β1y, α2x + β2y)
The second equality is a result of the fact that a linear transformation L is a homomorphism. The third equality is a result of the fact that L is homogeneous.
Section 4: Linear transformations and matrices
The coordinates mentioned in the previous section are actually coordinates of arrays attached to points. Those arrays are displayed horizontally such as (2,3), (0,0), (λ, σ), (x,y). But they may be considered as 1x2 matrices. As matrices they have transposes
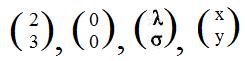 which are vertical arrays and are 2x1 matrices. These may be denoted by the horizontal notation
(2,3)t, (0,0)t, (λ, σ)t, (x,y)t
These arrays also attach themselves to points. Any horizontal array and its vertical transpose are attached to the same point. (But they are distinct arrays because the definition of matrix equality prohibits any equality of horizontal and vertical arrays.)
which are vertical arrays and are 2x1 matrices. These may be denoted by the horizontal notation
(2,3)t, (0,0)t, (λ, σ)t, (x,y)t
These arrays also attach themselves to points. Any horizontal array and its vertical transpose are attached to the same point. (But they are distinct arrays because the definition of matrix equality prohibits any equality of horizontal and vertical arrays.)
Now any linear transformation L is determined by the linear expressions
α1x + β1y and α2x + β2y
in its formula:
L(x,y) = (α1x + β1y, α2x + β2y)
But the expressions are completely determined by the coefficients in them:
α1, β1, α2, β2
Form a matrix from these coefficients. The first two coefficients become the top row, and the last two coefficients become the bottom row, and call the matrix M:
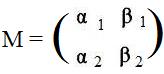
Example: If L is defined by L(x,y) = (2x + 3y, 5x - 2y) then
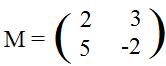
[4.1] (Associated matrix)sp3 Given a linear transformation which carries the arbitrary point (x,y) onto an array of linear expressions in x,y (formula). The matrix formed from the coefficients of these expressions, row 1 from the coefficients of the first expression, and row 2 from the coefficients of the second expression is the matrix associated with the linear transformation.
Notation: The matrix
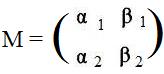 is the matrix associated with the linear transformation L defined by
L(x,y) = (α1x + β1y, α2x + β2y)
is the matrix associated with the linear transformation L defined by
L(x,y) = (α1x + β1y, α2x + β2y)
If L(x,y) = (α1x + β1y, α2x + β2y) then replace x,y by 1,0 and replace x,y by 0,1 to get
L(1,0) = (α1, α2) and
L(0,1) = (β1, β2)
These are the images of the special points. They appear as columns in matrix M.
[4.2] (Images of special points in the associated matrix)sp3 For a linear transformation, the images of the special points appear as columns in the associated matrix.
Notation: if L(1,0) = (α1, α2) and L(0,1) = (β1, β2) then the matrix associated with L is
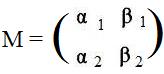
Example:
If L(1,0) = (5,8) and L(0,1) = (6,7) then the images of the special points are (5,8) and (6,7). The vertical arrays (5,8)t and (6,7)t become columns in the matrix associated with L:
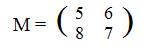 The formula for L is obtained in the usual way:
The formula for L is obtained in the usual way:
L(x,y) = xL(1,0) + yL(0,1) = x(5,8) + y(6,7) = (5x + 6y, 8x + 7y)
The same associated matrix M can be obtained from the coefficients of the linear expressions 5x + 6y and 8x + 7y.
It is no surprise that the identity matrix is the matrix associated with the identity linear transformation. The identity transformation I on the planesp3 carries each point onto itself, including the special points: I(1,0) = (1,0) and I(0,1) = (0,1). It is customary to let I denote both the identity linear transformation and its associated identity matrix.
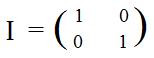
Notice that [4.1] and [4.2] provide two methods to obtain the matrix associated with a linear transformation.
But given the associated matrix, can the linear transformation with its formula be determined? Using the matrix M from the last example,
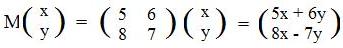 This product has reproduced the linear expressions 5x + 6y and 8x + 7y that are in the horizontal formula for L.
This product has reproduced the linear expressions 5x + 6y and 8x + 7y that are in the horizontal formula for L.
[4.3]sp3 The product of the matrix associated with a linear transformation and the vertical array (x,y)t produces a vertical array whose coordinates are the linear expressions in the formula for the linear transformation.
Notation: If the matrix M given in [4.2] is associated with a linear transformation L, then the vertical array produced by the product M(x,y)tin
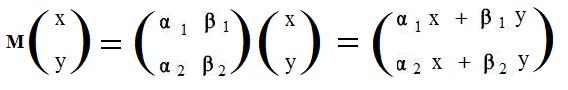 contains the same linear expressions as in the horizontal formula in L(x,y) = (α1x + β1y, α2x + β2y).
contains the same linear expressions as in the horizontal formula in L(x,y) = (α1x + β1y, α2x + β2y).
This equation shows the matrix M acting like a function, carrying vertical arrays onto vertical arrays. Intuitively speaking, a transformation L and its associated matrix M do the same thing. L carries horizontal array (x,y) onto some horizontal array (formula) containing linear expressions. The matrix M carries the vertical array (x,y)t onto a vertical array containing the same linear expressions as in the image L(x,y). The minor difference is that L works with horizontal arrays, and the associated matrix works with vertical arrays. But any point is carried onto the same point by L and by M.
Recall that the product (composition) of two linear transformations on the plane is defined as the second transformation carrying all the images of the first transformation into the plane. But the product of matrices also exists.
The following is a relationship between the two products:
[4.4] (Products of associated matrices)sp3 The matrix associated with the product of two linear transformations on the plane is equal to the product of the two matrices associated with each linear transformation, all taken in the same order.
Notation: if M1 and M2 are the matrices associated with the linear transformations L1
and L2 then the product M2M1 is the matrix associated with the product L2L1.
Notice that the product M2M1 is in the same order as the product L2L1 and not L1L2.
Click here for an argument supporting [4.4].
This statement [4.4] can be used as a convenient way to compute the product of two linear transformations. For example, suppose L1 and L2 are defined by
L1(x,y) = (6x+7y, 8x+9y) and L2(x,y) = (2x+3y, 4x+5y)
To find the image L2L1(x,y), first compute the product of their associated matrices:
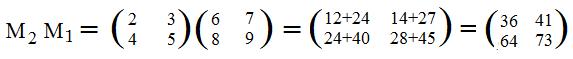 Then get the coefficients of the linear expressions from this last matrix on the right:
L2L1(x,y) = (36x+41y, 64x+73y)
Then get the coefficients of the linear expressions from this last matrix on the right:
L2L1(x,y) = (36x+41y, 64x+73y)
Section 5: Linear transformations that preserve distance
Note: Some discussions in this section will involve directed arcs and trigonometry. The reader may wish to review these topics.
Click here to go to the appendix.
It was discussed in an earlier section that a linear transformation carries segments onto segments (or onto points). However, the segments may or may not be congruent. But those linear transformations that do carry figures onto congruent figures deserve special study. They do not change the lengths of segments, and therefore do not change the distances between their endpoints.
[5.1] (Distance preserving) A linear transformation on the plane sp3 preserves distance if and only if the distance between the images of any two points is the same as the distance between the points themselves.
Notation: On any plane with an origin, L preserves distance if and only if for any points P,Q,
the distance between L(P) and L(Q) = distance between P and Q
Notation: On the coordinate plane, L preserves distance if and only if for all real numbers α,β, γ,δ,
distance between L(α,β) and L(γ,δ) = distance between (α,β) and (γ,δ)
Example 1: On any planesp3 the identity transformation I preserves distance. Every point is its own image: I(P)=P and I(Q)=Q. Then by simple substitution distance between I(P) and I(Q) = distance between P and Q.
Example 2: The linear transformation L that interchanges coordinates, L(x,y) = (y,x) preserves distance.
A simple proof shows that the distance between points (β,α) and (δ,γ) and the distance between points (α,β) and (γ,δ) are equal. Click here to see the computations.
A simple geometric interpretation for L in this example is given below in a discussion about reflections.
Example 3: The linear transformation L defined by L(x,y) = (x cos θ + y sin θ, -x sin θ + y cos θ) preserves distance.
It is possible to develop a proof based on the idea given in the previous example. Computation will show that
the square of the distance between points (α cos θ + β sin θ, -α sinθ + β cos θ) and (γ cos θ + δ sin θ, -γ sin θ + δ cos θ)
is equal to
the square of the distance between points (α,β) and (γ,δ)
However this fact will be proven in a following discussion of rotations about the origin.
Questionopt: Are there any distance preserving functions that are not linear transformations? The following gives a partial answer to this question. A complete answer will be given in chapter 6 in a discussiion about translations.
[5.2]opt Any function on the planesp3 that preserves distance and leaves the origin fixed is a linear transformation.
Click here to see a discussion supporting [5.2].
Let L be a linear transformation that preserves distance. Then L preserves the lengths of all radii the unit circle. This means L carries the unit circle back onto itself. The special points (1,0) and (0,1) are on this circle. Then their images L(1,0) and L(0,1) are somewhere on that circle (Fig 1). Since L preserves distance, the chord between the special points is congruent to the chord between the images. Therefore the length of arc between (1,0) and (0,1) is equal to the length of arc between those images.
There are two ways that the labels on the images can be occur.
One way is shown in Fig 2, where the directed arc from point L(1,0) to point L(0,1) has a counter-clockwise direction (bends to the left).
The other way is hown in Fig 3, where the directed arc from point L(1,0) to point L(0,1) has a clockwise direction (bends to the right).
[5._] (Preserving distance and orthogonal matrix) A linear transformation preserves distance if and only if its associated matrix is orthonormal.
[5._] (Preserving distance and inner product) A linear transformation preserves distance if and only if it preserves the inner product of every pair of position vectors.
Notation: for any position vectors p and q, L(p)*L(q) = p*q
Notation: for any position vectors p and q and their images p' and q', p'*q' = p*q.
(Click here for a discussion about directed arcs.)
========================================================
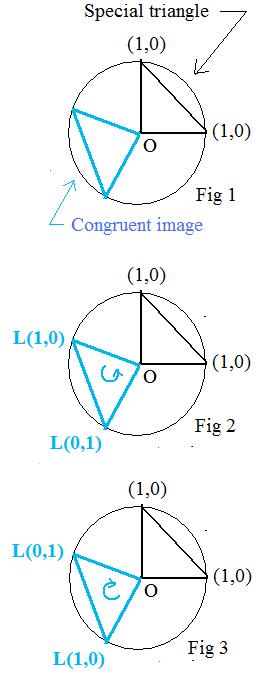
The special points are (1,0) and (0,1). They and the origin O are vertices of a right triangle, called the special triangle (Fig 1). Any distance preserving linear transformation L carries this triangle onto a congruent triangle that also has a right angle at the origin. As far as plane geometry is concerned, there is only one congruent triangle obtained from the special triangle. However using the labels attached to the vertices, there are two coincident image triangles. They are most easily distinguished by their orientations.
If the order of L(1,0), L(0,1), O gives a counter-clockwise orientation to the image triangle, then L has made the image triange from the special triangle by a rotation about the origin(Fig 2). Intuitively speaking, the special triangle has slid around the origin until it reaches the position of the image triangle.
If the order of L(1,0), L(0,1), O gives a clockwise orientation to the image triangle, then L has made the image triangle from the special triangle by a rotation about the origin and then a reflection about the bisector of the right angle at the origin.(Fig 3). Intuitively speaking, the special triangle has not only moved about the origin but also flipped so that the vertices, not the origin, interchange positions. The moving triangle settles down on the position of the image triangle.
 Let r = p + q. Then points O,P,R,Q are vertices of a parallelogram (the parallelogram of addition of vectors). Now L carries position vectors p,q,r onto position vectors p',q',r' and by [1.2a] r' = p' + q'. Therefore points O,P',R',Q'' are vertices of a parallelogram. Therefore, L carries the vertices of parallelogram OPRQ onto the vertices of parallelogram OP'R'Q'. Later, it will be shown that every linear transformation carries segments onto segments. Hence, every linear transformation carries parallelograms with one vertex on the origin onto parallelograms with one vertex on the origin.
Let r = p + q. Then points O,P,R,Q are vertices of a parallelogram (the parallelogram of addition of vectors). Now L carries position vectors p,q,r onto position vectors p',q',r' and by [1.2a] r' = p' + q'. Therefore points O,P',R',Q'' are vertices of a parallelogram. Therefore, L carries the vertices of parallelogram OPRQ onto the vertices of parallelogram OP'R'Q'. Later, it will be shown that every linear transformation carries segments onto segments. Hence, every linear transformation carries parallelograms with one vertex on the origin onto parallelograms with one vertex on the origin.