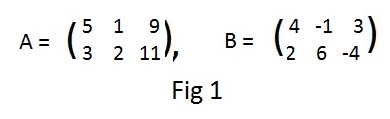Return to main page
Volume E Chapter 1
Additional Material
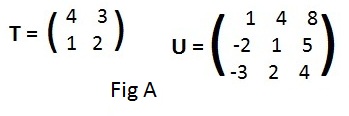
Getting Determinant Values of a 2x2 and 3x3 Matrix by Hand
The task is to obtain the determinant values of matrices T and U in Fig A without the use of the computer. The method used is called "cross-hatch>"
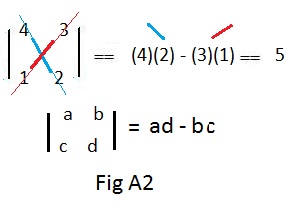 det (T) = 5.
det (T) = 5.
For detailed explanation of the method (see adjacent Fig A2):
Draw a slant line through the entries in the upper left and lower right. Form the product of these entries (8). Draw a slant line through the entries in the upper right and lower left. Form the product of these entries (3). From
From the first product subtract the second product: 8 - 3 = 5.
Also in Fig 2 is the general formula ad − bc for finding the determinant value of any 2x2 matrix.
A common notation for a determinant introduced here. It avoids using the name of the matrix and replaces the large parentheses ( ) by vertical lines | |.
 det(U) = -42
det(U) = -42
Copy columns 1 and 2 to the right of the determinant..
Draw a slant line (main diagonal) from the entry in the upper left (position [1,1]) down through the entry in the center of the determinant (position [2,2]) and down to the entry in the lower right (position[3,3]). Draw another slant line (main diagonal) from the top middle entry (position [1,2] parallel to the first slant line through two m9ore entries. Draw a third slant line from the top right entry parallel to the other two slant lines.
Format of a Saved Matrix - optional information
Sometimes it is useful to use again a matrix that was created earlier. The computer has stored the matrix in a file. Along with the matrix entries, the computer attached a name for the matrix and the size. Suppose the matrix is
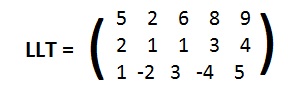 The name of this 3x5 matrix is "LLT". The matrix is stored as
[M "LLT", 3,5, 5,2,6,8,9, 2,1,1,3,4, 1,-2,3,-4,5]
The information between the brackets [ ] is called "data-input from the file". Often the phrase "from the file" will be omitted. The computer can restore the matrix from the "data-input". The letter M tells the computer that the data is for a matrix. The name of the matrix LLT appears between quotation marks. The next two numbers 3,5 give the size of the matrix. All the entries appear after that. Between rows for the matrix appear spaces.
The name of this 3x5 matrix is "LLT". The matrix is stored as
[M "LLT", 3,5, 5,2,6,8,9, 2,1,1,3,4, 1,-2,3,-4,5]
The information between the brackets [ ] is called "data-input from the file". Often the phrase "from the file" will be omitted. The computer can restore the matrix from the "data-input". The letter M tells the computer that the data is for a matrix. The name of the matrix LLT appears between quotation marks. The next two numbers 3,5 give the size of the matrix. All the entries appear after that. Between rows for the matrix appear spaces.
Matrices A and B are stored as
[M "A", 2,3, 5,1,9, 3,2,11], [M "B", 2,3, 4,-1,3, 2,6,-4]
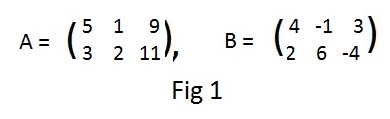
Matrix as shorthand for system of linear equations - optional information
Consider the following sets of linear equations in two unknowns:
(*)
5x + y = 9 5u + v = 9 5α + β = 9 A
3x + 2y = 11 3u + 2v = 11 3α + 2β = 11
Matrix A in Fig 1 contains the same numerical information from each set of equations. Each set is easily solved. Multiply the top equation by 2 and subtract the bottom equation from the result.
x = 1 u = 1 α = 1
y = 4 v = 4 β = 4
These solution-equations may be written as:

(**)
x + 0y = 1 u + 0v = 1 α + 0β = 1
0x + y = 4 0u + v = 4 0α + β = 4
The matrix W contains the numerical data from these equations.
The purpose of this discussion is to proceed from equations (*) to equations (**) using only matrices. However, the longer equations with letters will be written for comparison.

Since the matrices do not include x,y,+,= there is much less writing them. However, zeros are needed when a variable letter is absent from the cofrresponding equation. Also it is possible to have a computer do the matrix method of solving the equations. However, there are "better" methods to be discussed later.
A Motivation for Matrix Multiplication
The following linear equations show how to get values for x' and y' from values given to x and y:
(*) x' = x + 2y
y' = 3x - y
The following equations show how to get values for x" and y" from values given to x' and y':
(**) x" = 4x' +3y'
y" = 2x' - 4y'
Then values given to x and y eventually cause values to be given to x" and y". For example, if 1 and 3 are assigned to x and y respectively in equations (*) then x' and y' receive values 7 and 0. But if these values are given to x' and y' in equations (**) then x' and y" receive values 28 and 14. Derive the equaations that assign values to x" and y" directly from x and y.
The idea is simple: replace x' and y' in equations (**) by their equals in equations (*):
x" = 4(x + 2y) + 3(3x-y)
y" = 2(x + 2y) - 4(3x-y)
These equations simplify to:
(***) x" = 13x + 5y
y" = -10x + 8y
If 1 and 3 are assigned again to x and y but this time in equations (***) then x" and y" again receive the values 28 and 14.
The coefficient matrices for equations (**) and (*) are below and the computer gives their product on the right side of the equal sign. Notice that this product is equal to the coefficient matrix for equations (***).
Click here to see more on the motivation of the rule for multiplying matrices.
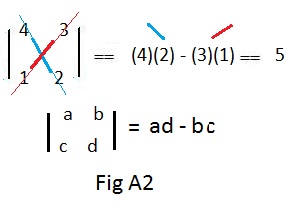 det (T) = 5.
det (T) = 5. 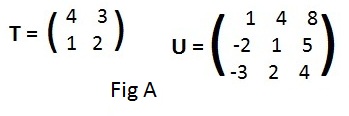
 det(U) = -42
det(U) = -42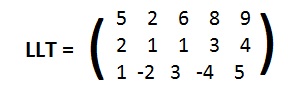 The name of this 3x5 matrix is "LLT". The matrix is stored as
The name of this 3x5 matrix is "LLT". The matrix is stored as