Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Drawing exercises
Computer Programs
Return to index of all chapters in this volume
Volume D Chapter 1
Geometric Vectors
This chapter introduces some of the basic facts about vectors in a very intuitive way, using drawn geometric figures, and observing some of their familiar properties. Therefore "discussions supporting statements" will be the phrase used instead of "proofs of statements." Yet, from these intuitive and elementary ideas there will be developed a very simple but limited algebra that will very closely resemble ordinary algebra taught in middle or early high school. In the next chapter where arrays are introduced, a more exact yet similar algebra will be developed. Moreover, a "tight" correspondence between geometric vectors and arrays will be developed, which will supply simple proofs to most all intuitive statements presented in this chapter about geometric vectors.
Section 1: Introduction to geometric vectors
In this section vectors are introduced intuitively using figures and some facts from high school geometry. Straight line segments and parallelograms play important roles in discussions. The reader is advised to click here to review some simple constructions of parallel lines and parallelograms in [1], [2a], [2b] there.
 A most simply drawn figure is the straignt line segment. It connects two points which are called the end-points of the segment. If A and B are points, then the line segment joins A and B. It has the symbol AB. Obviously BA denotes the same segment. The line through A and B uses the same symbols but with the "word" line before them: line AB = line BA. The length of a segment is the numerical distance between the end points. For segment AB, the symbol |AB| is its length. The length or distance is never negative (|AB| ≥ 0). But it is sometimes convenient to allow the end points of a segment to coincide. It becomes a single point (|AA| = 0). It is called a segment of zero length. For convenience it is still considered a segment. Conersely, having zero length forces the end points to coincide: if |AB| = 0 then A=B.
A most simply drawn figure is the straignt line segment. It connects two points which are called the end-points of the segment. If A and B are points, then the line segment joins A and B. It has the symbol AB. Obviously BA denotes the same segment. The line through A and B uses the same symbols but with the "word" line before them: line AB = line BA. The length of a segment is the numerical distance between the end points. For segment AB, the symbol |AB| is its length. The length or distance is never negative (|AB| ≥ 0). But it is sometimes convenient to allow the end points of a segment to coincide. It becomes a single point (|AA| = 0). It is called a segment of zero length. For convenience it is still considered a segment. Conersely, having zero length forces the end points to coincide: if |AB| = 0 then A=B.
Neither end point of a segment has any priority over the other. But sometimes it is convenient to indicate a path starting with one end-point and going in a single direction along a line segment to the other end-point. This motion gives a direction to the segment. An orientation is imposed on a line segment if one end-point is designated as the initial point and the other end-point is designated as the terminal point. These points are also called the tail and head respectively.
[1.1] (Geometric vector) A geometric vector is an oriented line segment with an initial point (tail) and terminal point (head). It is represented as an arrow drawn from the tail to the head, thus having a direction, called an orientation
vector = segment with an orientation
Notation: AB = a vector from tail A to head B.
Often velocity is indicated by a vector. The movement of an object is in some direction. A vector on paper can represent that direction. The speed can be represented by the length of a vector. New vectors are introduced as the object changes direction or speed.
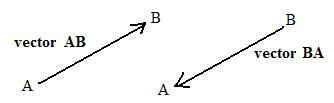 Symbols denoting vectors are printed in boldface. Symbols denoting segments appear lighter. AB is a vector, but its segment is AB. Without orientation segment AB is the same as segment BA. However, in general vector AB is different from vector BA because of different orientations: they point in opposite directions. (See adjacent figure.)
Symbols denoting vectors are printed in boldface. Symbols denoting segments appear lighter. AB is a vector, but its segment is AB. Without orientation segment AB is the same as segment BA. However, in general vector AB is different from vector BA because of different orientations: they point in opposite directions. (See adjacent figure.)
The symbol |AB| denotes the length of vector AB. Obviously, the vector and its segment have the same length: |AB| = |AB|.
If AB and CD are segments then the equation |AB| = 2|CD| says that AB is twice as long as CD. |AB| =3|CD| says that the length of vector AB has three times the length of vector CD. When the discussion involves only the lengths of vectors, the directions of the vectors are ignored. The vectors may be parallel, perpendicular, or pointing in any directions, different or same.
It may happen that the tail and head of a vector coincide: for example, AA where point A is both the tail and head of a vector. Then the vector has zero length |AA| = |AA| = 0, and its direction is undefined. Such a vector is called a zero vector. It is often denoted by a boldface zero: 0 Although a zero vector has no defined orientation, it will be assigned some strange properties in order than some statements involving it become shorter and more easily understood. For example, it will be convenient later to allow the zero vector to point in any direction. A vector with length not zero is called a non-zero vector. The tail and the head do not coincide for a non-zero vector.
Intuitively speaking, a geometric vector has both length and direction. Suppose now two vectors AB and CD have the same length and point in the same direction. With a compass it can be determined that they have the same length. Also they lie on parallel lines. By eyesight, they point in the same direction. They are "almost" equal, "almost" because they do not coincide. In many texts they are considered equal. More accurately, they are "equivalent". An intuitive description is as follows:
[1.2a] (Equivalent vectors - intuitive) Two geometric vectors are equivalent if and only if they have the same length and point in the same direction.
Notation: AB = CD
Because the equal sign is used, equivalent vectors are usually called equal.
By this concept a vector is equivalent to itself. For convenience, all zero vectors are considered equivalent.
Click here to see a construction and test for equivalent vectors.
 The definition of an ordinary parallelogram says that it is a quadrilateral with opposite sides parallel. But the following definition also includes the unusual idea of a "collapsed" parallelogram, which lies entirely on a line. There is a theorem from plane geometry that says that the opposite sides of a parallelogram have equal lengths. This will also be true for a "collapsed" triangle.
A,B,D,C are the vertices of any parallelogram then |AB| = |CD| and |AC| = |BD| which will be
true even for collapsed parallelogram A',B',D',C': |A'B'| = |C'D'| and |A'C'| = |B'D'|. The following definition includes the idea of a collapsed parallelogram.
The definition of an ordinary parallelogram says that it is a quadrilateral with opposite sides parallel. But the following definition also includes the unusual idea of a "collapsed" parallelogram, which lies entirely on a line. There is a theorem from plane geometry that says that the opposite sides of a parallelogram have equal lengths. This will also be true for a "collapsed" triangle.
A,B,D,C are the vertices of any parallelogram then |AB| = |CD| and |AC| = |BD| which will be
true even for collapsed parallelogram A',B',D',C': |A'B'| = |C'D'| and |A'C'| = |B'D'|. The following definition includes the idea of a collapsed parallelogram.
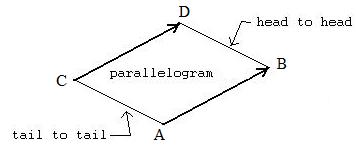 [1.2b] (Equivalent vectors - parallelogram method) For vectors not lying on a common line, they are equivalent if and only if the line segment joining the heads and the line segment joining the tails together with the two segments of the vectors form a parallelogram. For vectors lying on the same line, then a collapsed parallelogram is formed.
[1.2b] (Equivalent vectors - parallelogram method) For vectors not lying on a common line, they are equivalent if and only if the line segment joining the heads and the line segment joining the tails together with the two segments of the vectors form a parallelogram. For vectors lying on the same line, then a collapsed parallelogram is formed.
Notation: If AB = CD and AB and CD are on different lines, then ABDC is not a "collapsed" parallelogram. If AB and CD are on the same line, then ABDC forms a colapsed parallelogram. In either situation |AB| = |CD| and |AC| = |BD|.
If AB and CD coincide then they have the same initial points and the same terminal points. Therefore, (in the colapsed parallelogram,) |AC| = 0 and |BD| = 0. This shows that coincident vectors are equivalent. It can be shown that if a first vector is equivalent to a second, then the second vector is equivalent to the first. Finally, if the first vector is equivalent to a second, and the second is equivalent to a third, then the first vector is equivalent to the third. This means that equivalence defined in [1.2b] or described in [1.2a] is a true equivalence relation. (More exactly, equal vectors really means equal equivalence classes of equivalent vectors. But the reader may ignore this fact!)
***
 In most discussions of geometric vectors below a special fixed point O will have been chosen and called the origin. Its location usually is not important. In fact, it may even be missing in some figures. But it does have an important purpose.
In most discussions of geometric vectors below a special fixed point O will have been chosen and called the origin. Its location usually is not important. In fact, it may even be missing in some figures. But it does have an important purpose.
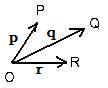
A vector is called a position vector if its tail (initial point) is on this origin O. For any points P,Q,R, the vectors OP, OQ, OR are position vectors, locating those points respectively. The corresponding lower case letters p,q,r will denote those position vectors respectively:
p = OP, q = OQ, r = OR.
Obviously, the point located by a position vector is actually the head (terminal point) of the position vector. The zero vector is the position vector of the origin:
0 = OO.
This means that there is a one-to-one correspondence between all points and the position vectors locating them. In other words,
[1.3] (Equality of position vectors) Two position vectors are equal if and only if they locate the same point.
Notation: Position vectors p = q if and only if points P = Q.
Usually, position vectors are easier to handle and often future discussions involve them rather than other vectors.
However, there exist vectors that are not position vectors, because their initial points are not on the origin. The vector AB is not a position vector if point A≠ O. In following discussions there are two ways that position vectors can be obtained "legally" from vectors not position vectors,
yet the metnods do not change the essential characteristics of the vectors.
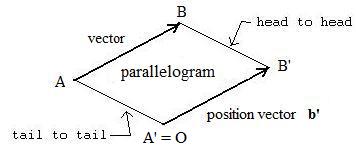 The first method is rather obvious: make a copy A'B' of the vector AB so that A' = O. With segment AB and point O construct a parallelogram with vertices A, B, B', O where B' is the unique point found during the construction. Click here for more details about this construction. The vector OB' = AB and OB' = b' is a position vector. Notice that only one position vector is equal to the given vector AB which is not a position vector.
The first method is rather obvious: make a copy A'B' of the vector AB so that A' = O. With segment AB and point O construct a parallelogram with vertices A, B, B', O where B' is the unique point found during the construction. Click here for more details about this construction. The vector OB' = AB and OB' = b' is a position vector. Notice that only one position vector is equal to the given vector AB which is not a position vector.
[1.4] (Equivalency to position vectors) Any vector is equal to a unique position vector.
A different method of creating position vectors from other vectors will be given below (see [1.10]) after subtraction of vectors has been introduced.
The major purpose of [1.4] is to show that any work with vectors anywhere can be intuitively "moved" to the origin without losing any characteristics of vectors involved.
The figure demonstrating the copying and moving action generates a parallelogram. This suggests a construction using a parallelogram for the geometric sum of two position vectors. Certain situations involving vectors in physics suggest this same sum.
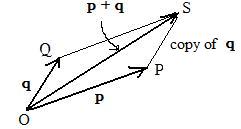 [1.4a] (The addition parallelogram for two position vectors) To add two position vectors, not on the same line, construct a parallelogram out of their head points and the origin. The diagonal from the origin becomes the vector which is the desired sum.
[1.4a] (The addition parallelogram for two position vectors) To add two position vectors, not on the same line, construct a parallelogram out of their head points and the origin. The diagonal from the origin becomes the vector which is the desired sum.
If the two position vectors are on the same line then use the triangle method [1.4b] given below.
Often the vector which is a vector sum of other vectors is called the resultant.
Notation: p + q is the sum of position vectors p and q.
To obtain the vector sum of two position vectors, not on the same line, form a parallelogram from the insecting lines containing the vectors and lines through the terminal points and parallel to these vectors. The vector sum is equal to the diagonal from the origin. Click here for more details about the construction.
A slight change to the parallelogram method produces another geometric method for producing the vector sum from two given vectors. In this situation a triangle is formed from half of the parallelogram.
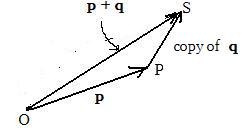 [1.4b] (Triangle method of addition of two vectors) To add two vectors, place the initial point (tail) of the second vector on the terminal point (head) of the first vector. Then the vector obtained by drawing a vector from the initial point (tail) of the first vector to the terminal point (head) of the second vector is the sum of the two given vectors.
[1.4b] (Triangle method of addition of two vectors) To add two vectors, place the initial point (tail) of the second vector on the terminal point (head) of the first vector. Then the vector obtained by drawing a vector from the initial point (tail) of the first vector to the terminal point (head) of the second vector is the sum of the two given vectors.
Notation: p + q is the sum of position vectors p and q.
Click here for more details about the construction.
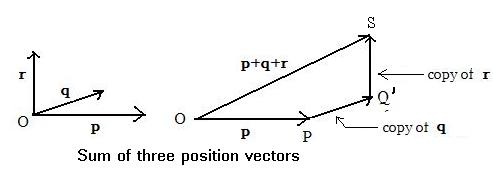 Sometimes there is a need to add three position vectors. But the methods of addition given in [1.4a] and [1.4b] show how to add two vectors. This minor problem is resolved by indicating which pair of vectors are to be added together before the third vector is added. The symbols to indicate the sum of three position vectors involve two addition signs. The following statement shows that either addition sign may be used before the other. In either situation, the triangle method is used twice to find the sum of three position vectors.
Sometimes there is a need to add three position vectors. But the methods of addition given in [1.4a] and [1.4b] show how to add two vectors. This minor problem is resolved by indicating which pair of vectors are to be added together before the third vector is added. The symbols to indicate the sum of three position vectors involve two addition signs. The following statement shows that either addition sign may be used before the other. In either situation, the triangle method is used twice to find the sum of three position vectors.
[1.5] (Vector addition is associative) For any three position vectors, the sum of the first two added to the third is equivalent to the first added to the sum of the second and third.
Notation: (p + q) + r = p + (q + r).
The discussion supporting [1.5] involves two diagonals of a quadrilateral. In the figure the diagonals OQ' and
PS are not drawn.
The vector OQ' = p + q and the vector OS = OQ' + r = (p + q) + r.
Similarly, PS = q + r and the vector OS = p + PS =
p + (q + r).
Since OS = OS then (p + q) + r = p + (q + r).
The following statement is a trivial consequence of the triangle method of addition:
[1.6] (Additive identity) The sum of any vector and the zero vector is that first vector. The sum of the zero vector and any vector is that second vector.
Notation: p + 0 = p and 0 + q = q
It is quite possible that the sum of two position vectors is the zero vector.
[1.7a] (Additive inverse) If the sum of two position vectors is the zero vector then each of those vectors is the additive inverse of the other.
Notation: if p + q = 0 then q is the additive inverse of p and p is the additive inverse of q.
Because 0 + 0 = 0, the zero vector is its own additive inverse.
The use of the word "the" in the phrase "the additive inverse" assumes that the additive inverse is unique. Click here for a discussion that supports this uniqueness. That discussion involves the negative of a posistion vector, which is discussed next.
In volumn B about integers, the negative -n of any natural number n was found on the same line as n, but on the other side of the origin O. The distance between -n and the origin O was equal to the distance between n and the origin. This same idea can be extended to position vectors.
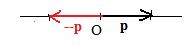 [1.7b] (The negative of a position vector) The negative of a given position vector is a position vector that has the same length but opposite direction as the given position vector.
[1.7b] (The negative of a position vector) The negative of a given position vector is a position vector that has the same length but opposite direction as the given position vector.
Notation: −p is the negative of p.
Click here to see the construction of the negative.
[1.7c] (The negative is the additive inverse) The negative of any position vector is the additive inverse of that vector.
Notation: −p is the additive inverse of p.
The statements [1.7a] and [1.7c] combine to say that the only way that the sum of two position vectors be the zero vector is that the two vectors have equal lengths and opposite directions.
The four statements [1.4b], [1.5], [1.6], [1.7c] satisfy the axioms for a group. The following statement shows that it is a commutative group. (It is a convention that all additive groups be commutative.)
[1.8] (Vector addition is commutative) The sum of a first position vector and a second position vector is the same as the sum of the second position vector and the first position vector.
Notation: p + q = q + p

The addition parallelogram for two vectors shows commutativity. The addition in the lower half triangle and the addition in the upper half triangle produce the same diagonal vector:
p + q = OP + PS = OS q + p = OQ + QS = OS
Since OS = OS then p + q = q + p.
The statement [1.7c] describes an additive inverse (negative) for any vector. This allows the following definition:
[1.9] (Vector subtraction) To subtract a second vector from a first vector add the additive inverse (negative) of the second vector to the first vector.
Notation: p − q = p + (−q).
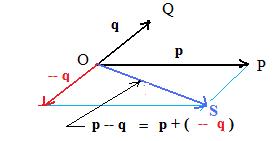
This equation gives the directions for constructing the difference p − q from the given vectors p and q. Construct the inverse − q of q. The add p and − q. The figure to the right shows the vector sum OS obtained by using the parallelogram method.
A little more can be "squeesed" out of this figure for vector subtraction. Not drawn is the vector QP drawn from points Q to P. But position vectors q and p, respectively, locate these two end points of QP. It is easily shown that QP and OS are equivalent. Therefore, QP = p − q.
[1.10] (Difference of position vectors) Any vector is equivalent to a position vector obtained by subtraction of the position vector to the initial point(tail) from the position vector to the terminal point (head).
Notation: QP = p − q.
This idea will be used many times in discussions later. It may be useful to memorise:
any vector = the position vector to its head minus the position vector to its tail.
Notice that order of the subraction p − q is given in the reverse order of the notation of the vector QP.
The following is trivial and comes as no surprise.
[1.11] (Subtraction of a position vector from itself) The subtraction of a position vector from itself produces the zero vector.
Notation: p − p = PP = 0
Another method to derive the equation in [1.10]: by the triangle method of addition, q + QP = p. Subtract q from both sides to get 0 + QP = p − q.
In working with drawn vectors and their equations, the rules of elementary often are assumed. For example, it is easy to show that PQ = − QP because PQ = q − p and QP = p − q. The reader can finish the argument.
***
The reader may have noticed that in equations vectors behave much like numbers: adding, subtraction, additive identitiy,,... And yet, statements about vectors in this section come from drawings or come from other statements that come from drawings.
An intuitive approach to the following definition can be found by clicking here.
[1.12] (Multiplication of a vector by a number) The product of a given number and a given position vector is a position vector whose length is the product of the absolute value of the given number and the length of the given position vector. The direction of the product is determined as follows:
(a) if the number is positive then the product and the given vector point in the same direction.
(b) if the number is zero (or the vector is 0) then the product is the zero vector, the direction of which is not defined
(c) if the number is negative then the product and the given vector have opposite directions.
Notation: |λp| = |λ| |p| .
if λ>0 then λp and p point in the same direction;
if λ=0 (or p = 0) then λp = 0
if λ<0 then λp and p point in opposite directions.
[1.13] (Coefficients and terms) In the product of a real number and a position vector, the real number is called a coefficient and the product is called a term.
For the expressions 3p and −4q the numbers a 3 and −4 are coefficients of the terms 3p and − 4q.
Any vector by itself is a term with coefficient 1: p = 1p. Any negative vector is a term with coefficient −1: −q = (−1)q.
Appropriate drawings can be assumed to support the following distributive laws. However, their proofs must await the discussion of arrays.
[1.14] (Zero term) A term is equal to the zero vector if and only if either the coefficient is the zero real number or the vector is the zero vector (or both).
Notation: λp = 0 if and only if λ = 0 or p = 0.
If 2p = 0 then p must be the zero vector. If λq = 0 and q q ≠ 0, then λ = 0.
[1.15] (Commutativity of coefficients) If the product of two real numbers multiplies a position vector, then the product of the real numbers can be expressed in either order.
Notation: (λσ)p = (σλ)p.
[1.16] (Right distributive law for multiplication by real numbers) If the sum of two real numbers is the coefficient of a position vector, then that product is equal to the sum of products of each number and the vector.
Notation: (λ + σ)p = λp + σp
Simple arithmetic shows that (3 + 2)p = 3p + 2p. Click here to see a very simple argument involving counting that supports this statement and the next statement for coefficients that are positive integers.
[1.17] (Left distributive law for multiplication by real numbers) The product of a real number and the sum of two position vectors is equal to the sum of the products of the real number and each vector.
Notation: λ(p + q) = λp + λq
Simple arithmetic shows that 2(p + q) = 2p + 2q
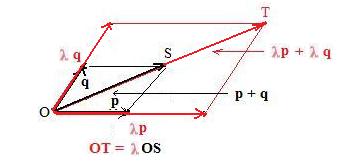
The geometric interpretation of this law [1.17] involves the geometric idea of similar figures. Intuitively, the multiplication by the coefficient λ expands or contracts uniformly the addition parallelogram of the two vectors. (If λ is negative then the parallelogram is also reflected through the origin O.)
There are obvious extensions to the statements about distributive laws.
(λ + σ + ω + . . .)p = λp + σp + ωp + . . .
λ(p + q + r + . . .) = λp + λq + λr + . . .
and a combination of them:
(λ + σ)(p + q) = λp + λq + σp + σq.
(λ − σ)(p − q) = λp − λq − σp + σq.
Obviously, the rules of elementary high school algebra still apply.
Section 2: Some elementary vector geometry: points on a line
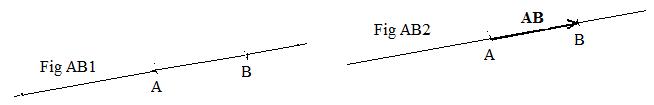 Through two distinct fixed points A and B (|AB|≠0) a single line can be drawn (Fig AB1). A vector AB joins A to B (Fig AB2).
Suppose a point P lies anywhere on the line through A and B. Form the quotient |AP|/|AB| which is always possible since A and B are different points. Let the real number λ equal this quotient if vectors AP and AB point in the same direction and let λ equal the negative of this quotient if AP and AB point in the opposite direction. Then by [1.12],
(&) AP = λAB
Through two distinct fixed points A and B (|AB|≠0) a single line can be drawn (Fig AB1). A vector AB joins A to B (Fig AB2).
Suppose a point P lies anywhere on the line through A and B. Form the quotient |AP|/|AB| which is always possible since A and B are different points. Let the real number λ equal this quotient if vectors AP and AB point in the same direction and let λ equal the negative of this quotient if AP and AB point in the opposite direction. Then by [1.12],
(&) AP = λAB
 This vector equation forces vectors AP and AB to lie on the same line through A and B. Changing the values of λ will cause AP to stretch or shrink or even point in the opposite direction of AB.
If λ is between 0 and 1 then P is between A and B (Fig AP3).
This vector equation forces vectors AP and AB to lie on the same line through A and B. Changing the values of λ will cause AP to stretch or shrink or even point in the opposite direction of AB.
If λ is between 0 and 1 then P is between A and B (Fig AP3).
If λ > 1 then P is beyond B, so that B is between A and P (Fig AP4)
If λ < 0 then P is beyond A, so that A is between P and B (Fig AP5)
Looking at equation (&) above where AB≠0 , point P will coincide with A if and only if λ is given the value 0 because AP = 0.
Also point P will coincide with B if and only if λ is given the value 1 because AP = AB
Suppose 0 < λ < 1. which means that point P lies in the interior of segment AB (Fig AP3), which is the situation often in the discussions in this section. Using motion to help explanations, λ tells how far P is along the path from A to B because λ = |AP|/|AB|. In particular, if λ = 1/2 then P has gone half the way from A to B. In other words, P is midway between A and B. P is the mid point of segment AB. In the following discussion M is used for midpoint instead of point P.
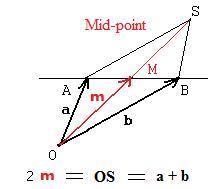
Given two points A and B on a straight line. A mid point M is half the distance from A to B. So vector AM = (1/2)AB. This is equivalent to saying 2AM = AB. By [1.9] this can be written 2(m − a) = b − a. Simple algebra can be used to solve for 2m. Then 2m = a + b. Finally, m = (a + b)/2.
[2.2] (Mid point) The position vector locating the point mid way between two given points is the sum of the position vectors to those given points divided by 2.
Notation: if A and B are given points, then the following position vector locates the point mid way on the line segment between A and B :
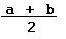
Roughly speaking, the arithmetic average of two position vectors locates the mid point. Let the reader derive the same formula for mid-point from the fact that vectors AM = MB. M is also the mid point of OS because 2AM = AB. So [2.2] shows also that the diagonals of a parallelogram bisect each other.
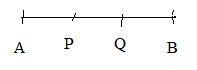 Now consider a point that is 1/3 the way from one end point of a segment to the other end point. Such a point is called a point of trisection of the segment nearest to the first end point. It too has a position vector locating it in terms of the end points of the segment.
Now consider a point that is 1/3 the way from one end point of a segment to the other end point. Such a point is called a point of trisection of the segment nearest to the first end point. It too has a position vector locating it in terms of the end points of the segment.
[2.3] (Point of trisection) The two points P,Q of trisection of the segment between points A and B are located by the position vectors
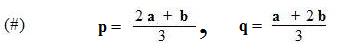
Let P and Q be the points of trisection of segment AB as shown. Then P is 1/3 the way from A to B, that is, AP = (1/3)AB. The inline equation 3AP = AB is equivalent. This equation, in turn, is equivalent to 3(p − a) = b − a. Solving for p produces the first equation in:
(##)
p = 2a + b 3q = a + 2b
Dividing the equation by 3 shows that p is equal to the first fraction in (#). Moreover the point P is nearer to A, because it is only 1/3 the way from A to B. The 2 in term 2a, gives the term more weight, so P is "pulled" closer to A and awa from B.
Similarly, BQ = (1/3)BA leads to the second equation in (##) and dividing by 3 shows that q is equal to the second fraction in (#). Also Q is closer to B than A because of the 2 in the term 2b.
If the 5 points P1, P2, P3, P4, P5 separate the segment AB internally into 6 congruent parts, then the five equations
AP1 = (1/6)AB, AP2 = (2/6)AB, AP3 = (3/6)AB, AP4 = (4/6)AB, AP5 = (5/6)AB
lead to the five inline equations, respectively,
(%)
6p1 = 5a + b, 6p2 = 4a + 2b, 6p3 = 3a + 3b, 6p4 = 2a + 4b, 6p5 = a + 5b
Dividing by 6 produces the following position vectors to each of the 5 points P1, P2, P3, P4, P5 respectively:
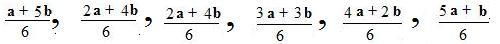
Several of the equations in (%) can be simplified. For example, the second equation may be divided by 2 to produce the inline equation 3p2 = 2a + b which says that P2 is a point of trisection of AB nearest to point A. Similarly, by dividing the middle equation in (%) by 3, P3 is a mid point of segment AB.
The inline equations in (%) all have the form
np = αa + βb
where α + β = n. The number n = the number of congruent intervals that partition the segment AB. The numbers α and β assume values 1,2,...,n-1 and n-1, n-2, ... ,1. Replace n by its equal α + β to get a general form:
(%%)
(α + β)p = αa + βb
[2.4] Let A and B be any distinct points and P any point. Let α and β be any real numbers whose sum is not zero. Let λ also be a real number. Then the equations
AP = λAB and
(α + β)p = αa + βb
are equivalent if and only if
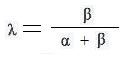
Click here to see the discussion supporting this statement.
Example1: if 7p = 3a + 4b then λ = 4/(3 + 4) = 4/7. So AP = (4/7)AB, and point P is 4/7 the way from A to B.
Example2: if AP = (6/11)AB then 6/11 = λ = β/(α + β). Then β = 6, α + 6 = 11. So α = 5. Therefore (5 + 6)p = 5a + 6b. This example can also be done by replacing AP and AB in the equation AP = (6/11)AB by their respective differences of position vectors p − a and b − a and solving for 11p.
* * *
The arithmetic average of vectors can be given geometric meanings. The average of two quantities is their sum divided by 2. The average of three quantities is their sum divided by 3. The average of four quantities is their sum divided by 4. The quantities can be position vectors as well as numbers:
(a + b/2, (a + b + c)/3,
(a + b + c + d)/4
The average of two position vectors a,b is a position vector pointing to the mid point M of segment AB. The average of three position vectors a,b,c is the object of this discussion. Let g be that average. Then the inline equation for this average is
3g = a + b + c
What is the geometric meaning of the point G to which g points?
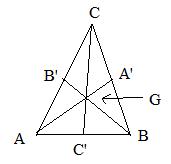 To answer this question form a triangle using the points A,B,C as vertices. Assume that not all points are one line. Now construct the medians to all three sides: find the mid point A' of side BC, mid point B' of side AC, and mid point C' of side AB. The medians are line segments AA', BB', CC' drawn from the vertices to these mid points. Using the inline notation for position vectors pointing to mid points:
To answer this question form a triangle using the points A,B,C as vertices. Assume that not all points are one line. Now construct the medians to all three sides: find the mid point A' of side BC, mid point B' of side AC, and mid point C' of side AB. The medians are line segments AA', BB', CC' drawn from the vertices to these mid points. Using the inline notation for position vectors pointing to mid points:
2a' = b + c,
2b' = a + c, 2c' = a + b
The right side of each equation will become equal to a + b + c if a is added to both sides of the first equation, b to both sides of the second equation and c to both sides of the last equation. The equations become:
2a' + a = a + b + c,
2b' + b = a + b + c,
2c' + c = a + b + c
which is the same as
2a' + a = 3g,
2b' + b = 3g,
2c' + c = 3g
By [2.4] the equivalent equations are:
A'G = (1/3)A'A, B'G = (1/3)B'B, C'G = (1/3)C'C
Therefore G is a point of trisection of segment AA' nearest A'. The same point G is a point of trisection of segment BB' nearest B'. The same point G is a point of trisection of segment CC' nearest C'. The common point G is called the centroid of the triangle. If the triangle is cut out exactly from metal of uniform thickness, then the cutout will balance on a vertical pinpoint pointing to the centroid.
[2.5a] (Intersection of the medians of a triangle) The medians of a triangle intersect at a common point. Moreover, that point is the point of trisection nearer to the sides of the triangle and further from the vertices.
The discussion before [2.5a] also supports the following statement
.
[2.5b] Three times the position vector to the point of intersection of the medians is equal to the sum of the position vectors to the three vertices of the triangle.
Notation: For triangle with vertices A,B,C and if G is the common intersection of the medians, then 3g = a + b + c.
In the discussion above: 2a' = b + c and 2a' + a = 3g. Substitution removes 2a' from the picture to get 3g = a + b + c.
The average of four position vectors to the vertices of a tetrahedron (in space) locates the centroid of that tetrahedron. It is left as an exercise. Click here to go to that exercise.
Section 3: Linear combinations of geometric vectors
Recall that a term is a single position vector (positive or negative) or a product of a real number and a position vector. In the previous section sums of such terms have been discussed. For example, 4a + 2b is a sum of two terms. It is possible to have sums of more than two terms.(Subtraction can be realized by using negative real numbers as coefficients to produce negative terms). The following is a very important concept in discussions of vectors.
[3.1] (Linear combinations) A linear combination of vectors is a (finite) sum of terms. The real numbers in each term are the coefficients in the linear combination.
Notation: If α, β, γ, δ,... are real numbers and a, b, c, d, ... are position vectors then
αa + βb + γc + δd + ... is a linear combination of vectors a, b, c, d, ... with coefficients α, β, γ, δ,... respectively.
Abbreviation: lincomb = linear combination
Examples: 4a + 2b − 3c and (3/2)a + sqrt(2)b + 109c + d are lincombs of a, b, c, d. (The term 0d could be added to the first lincomb.)
Recall the triangle method [1.4b] for adding position vectors,
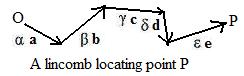 placing the tail of a position vector (term) on the head of the preceding position vector (term). This method of addition produces a direct path from the origin to the head of the final vector (term). That vector locates a point. The entire lincomb locates that same point. In the figure to the right in which copies are made of the terms βb, γc δd, εe, the lincomb
placing the tail of a position vector (term) on the head of the preceding position vector (term). This method of addition produces a direct path from the origin to the head of the final vector (term). That vector locates a point. The entire lincomb locates that same point. In the figure to the right in which copies are made of the terms βb, γc δd, εe, the lincomb
αa + βb + γc + δd + εe
locates the point P. The lincomb forms a directed path from O to P. (The path does not go from P to O.)
Some lincombs are equal to zero. This means that the lincombs locate the origin. Then the path is a loop, starting with the origin and ending with that same origin.
Each lincomb locates a point. It is quite possible that two (or more) different lincombs locate the same point. They form paths to the same point. Obviously, locating the same point is an equivalence relation. Therefore, two lincombs are equivalent if all the terms in each add up to the same vector. (Again the equal sign will be used.) The lincombs
αa + βb + γc + δd and λu + σv + ωw
are equivalent if and only if
αa + βb + γc + δd = λu + σv + ωw
Sometimes the sums of coefficients of lincombs are equal. This too will have a geometric interpretation.
[3.2] (Scalar balance) Lincombs are in scalar balance if and only if the sums of coefficients of each lincomb are equal.
Notation:
linear combinations
a + βb + γc + δd and λu + σv + ωw are in scalar balance
if and only if
the coefficients add up to be equal: α + β + γ + δ = λ + σ + ω
For example, the lincombs 6p and 4a + 2b are in scalar balance because 6 = 4 + 2.
But the linear combinations 5a + 3b + c and 4u + 7v are not in scalar balance because 5 + 3 + 1 is not equal to 4 + 7.
The lincombs 3a + 4b − 7c and 5c − 5d are in scalar balance because 3 + 4 − 7 = 0 = 5 − 5. But the zero sums will cause problems. So useful scalar balances will be non-zero scalar balances. The sums of coefficients will be not zero.
Lincombs in scalar balance almost always occur as sides of equations. Hereafter, equations showing equal lincombs are in scalar balance if and only if the lincombs that are the two sides of the equation are in scalar balance.
The equation
(@) 2a + 3b = 4c + d
is in non-zero scalar balance, because 2 + 3 = 4 + 1. But the vectors a,b and c,d are position vectors locating points A,B and C,D, which determine two lines, one through A,B and the other through C,D. Now introduce a position vector p such that
5p = 2a + 3b = 4c + d
There are two equations in scalar balance. Question: where is the point P located by position vector p? Since the equations
5p = 2a + 3b, 5p = 4c + d
are in scalar balance, point P is on both lines. Therefore position vector p locates the point of intersection AB ∩ CD of both lines.
The equation
2a + 3b − 4c − d = 0
can be obtained fromm the above equation (@) by subtracting the right side from the left side. Notice that the sum of the coefficients in this new equation equals zero.
If a lincomb equals 0 and the sum of all of its coefficients equals 0, then the lincomb is said to be a doubly zero lincomb.
There is a close relationship beetween doubly zero lincombs and equations in scalar balance.
[3.3] (Doubly zero lincombs) A lincomb with non-zero coefficients is doubly zero if and only the lincomb of some of its terms equals a lincomb of the remaining terms and the equation is in scalar balance.
If the lincomb
αa + βb + γu + δv + εw = 0
and the sum of its coefficients
α + β + γ + δ + ε = 0
then the lincomb is doubly zero. The lincomb is equivalent to the equation of lincombs
αa + βb = −γu − δv − εw
The equation is in scalar balance because
α + β = −γ − δ − ε
[3.4] Three points are collinear if and only if there exists a non-trivial, doubly zero lincomb of them.
Notation: A,B,C lie on the same line if and only if there exists a lincomb
αa + βb + γc = 0 α, β, γ not all zero
and
α + β + γ = 0
If coefficients 3,4,-7 have been found to satisfy 3a + 4b − 7c = 0, then the points A,B,C located by position vectors a,b,c are collinear.
Notice that this linear combination is equivalent to 7c = 3a + 4b which forces point C to be on line AB, 4/7 the way from A to B.
Click here to see a discussion of position vectors and planes in space.
 A most simply drawn figure is the straignt line segment. It connects two points which are called the end-points of the segment. If A and B are points, then the line segment joins A and B. It has the symbol AB. Obviously BA denotes the same segment. The line through A and B uses the same symbols but with the "word" line before them: line AB = line BA. The length of a segment is the numerical distance between the end points. For segment AB, the symbol |AB| is its length. The length or distance is never negative (|AB| ≥ 0). But it is sometimes convenient to allow the end points of a segment to coincide. It becomes a single point (|AA| = 0). It is called a segment of zero length. For convenience it is still considered a segment. Conersely, having zero length forces the end points to coincide: if |AB| = 0 then A=B.
A most simply drawn figure is the straignt line segment. It connects two points which are called the end-points of the segment. If A and B are points, then the line segment joins A and B. It has the symbol AB. Obviously BA denotes the same segment. The line through A and B uses the same symbols but with the "word" line before them: line AB = line BA. The length of a segment is the numerical distance between the end points. For segment AB, the symbol |AB| is its length. The length or distance is never negative (|AB| ≥ 0). But it is sometimes convenient to allow the end points of a segment to coincide. It becomes a single point (|AA| = 0). It is called a segment of zero length. For convenience it is still considered a segment. Conersely, having zero length forces the end points to coincide: if |AB| = 0 then A=B.
 Symbols denoting vectors are printed in boldface. Symbols denoting segments appear lighter. AB is a vector, but its segment is AB. Without orientation segment AB is the same as segment BA. However, in general vector AB is different from vector BA because of different orientations: they point in opposite directions. (See adjacent figure.)
Symbols denoting vectors are printed in boldface. Symbols denoting segments appear lighter. AB is a vector, but its segment is AB. Without orientation segment AB is the same as segment BA. However, in general vector AB is different from vector BA because of different orientations: they point in opposite directions. (See adjacent figure.)
 The definition of an ordinary parallelogram says that it is a quadrilateral with opposite sides parallel. But the following definition also includes the unusual idea of a "collapsed" parallelogram, which lies entirely on a line. There is a theorem from plane geometry that says that the opposite sides of a parallelogram have equal lengths. This will also be true for a "collapsed" triangle.
A,B,D,C are the vertices of any parallelogram then |AB| = |CD| and |AC| = |BD| which will be
true even for collapsed parallelogram A',B',D',C': |A'B'| = |C'D'| and |A'C'| = |B'D'|. The following definition includes the idea of a collapsed parallelogram.
The definition of an ordinary parallelogram says that it is a quadrilateral with opposite sides parallel. But the following definition also includes the unusual idea of a "collapsed" parallelogram, which lies entirely on a line. There is a theorem from plane geometry that says that the opposite sides of a parallelogram have equal lengths. This will also be true for a "collapsed" triangle.
A,B,D,C are the vertices of any parallelogram then |AB| = |CD| and |AC| = |BD| which will be
true even for collapsed parallelogram A',B',D',C': |A'B'| = |C'D'| and |A'C'| = |B'D'|. The following definition includes the idea of a collapsed parallelogram.
 [1.2b] (Equivalent vectors - parallelogram method) For vectors not lying on a common line, they are equivalent if and only if the line segment joining the heads and the line segment joining the tails together with the two segments of the vectors form a parallelogram. For vectors lying on the same line, then a collapsed parallelogram is formed.
[1.2b] (Equivalent vectors - parallelogram method) For vectors not lying on a common line, they are equivalent if and only if the line segment joining the heads and the line segment joining the tails together with the two segments of the vectors form a parallelogram. For vectors lying on the same line, then a collapsed parallelogram is formed. In most discussions of geometric vectors below a special fixed point O will have been chosen and called the origin. Its location usually is not important. In fact, it may even be missing in some figures. But it does have an important purpose.
In most discussions of geometric vectors below a special fixed point O will have been chosen and called the origin. Its location usually is not important. In fact, it may even be missing in some figures. But it does have an important purpose. The first method is rather obvious: make a copy A'B' of the vector AB so that A' = O. With segment AB and point O construct a parallelogram with vertices A, B, B', O where B' is the unique point found during the construction. Click
The first method is rather obvious: make a copy A'B' of the vector AB so that A' = O. With segment AB and point O construct a parallelogram with vertices A, B, B', O where B' is the unique point found during the construction. Click  [1.4a] (The addition parallelogram for two position vectors) To add two position vectors, not on the same line, construct a parallelogram out of their head points and the origin. The diagonal from the origin becomes the vector which is the desired sum.
[1.4a] (The addition parallelogram for two position vectors) To add two position vectors, not on the same line, construct a parallelogram out of their head points and the origin. The diagonal from the origin becomes the vector which is the desired sum. [1.4b] (Triangle method of addition of two vectors) To add two vectors, place the initial point (tail) of the second vector on the terminal point (head) of the first vector. Then the vector obtained by drawing a vector from the initial point (tail) of the first vector to the terminal point (head) of the second vector is the sum of the two given vectors.
[1.4b] (Triangle method of addition of two vectors) To add two vectors, place the initial point (tail) of the second vector on the terminal point (head) of the first vector. Then the vector obtained by drawing a vector from the initial point (tail) of the first vector to the terminal point (head) of the second vector is the sum of the two given vectors. Sometimes there is a need to add three position vectors. But the methods of addition given in [1.4a] and [1.4b] show how to add two vectors. This minor problem is resolved by indicating which pair of vectors are to be added together before the third vector is added. The symbols to indicate the sum of three position vectors involve two addition signs. The following statement shows that either addition sign may be used before the other. In either situation, the triangle method is used twice to find the sum of three position vectors.
Sometimes there is a need to add three position vectors. But the methods of addition given in [1.4a] and [1.4b] show how to add two vectors. This minor problem is resolved by indicating which pair of vectors are to be added together before the third vector is added. The symbols to indicate the sum of three position vectors involve two addition signs. The following statement shows that either addition sign may be used before the other. In either situation, the triangle method is used twice to find the sum of three position vectors.
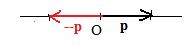 [1.7b] (The negative of a position vector) The negative of a given position vector is a position vector that has the same length but opposite direction as the given position vector.
[1.7b] (The negative of a position vector) The negative of a given position vector is a position vector that has the same length but opposite direction as the given position vector.

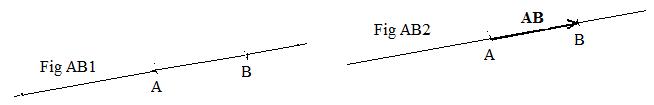 Through two distinct fixed points A and B (|AB|≠0) a single line can be drawn (Fig AB1). A vector AB joins A to B (Fig AB2).
Suppose a point P lies anywhere on the line through A and B. Form the quotient |AP|/|AB| which is always possible since A and B are different points. Let the real number λ equal this quotient if vectors AP and AB point in the same direction and let λ equal the negative of this quotient if AP and AB point in the opposite direction. Then by [1.12],
Through two distinct fixed points A and B (|AB|≠0) a single line can be drawn (Fig AB1). A vector AB joins A to B (Fig AB2).
Suppose a point P lies anywhere on the line through A and B. Form the quotient |AP|/|AB| which is always possible since A and B are different points. Let the real number λ equal this quotient if vectors AP and AB point in the same direction and let λ equal the negative of this quotient if AP and AB point in the opposite direction. Then by [1.12],
 This vector equation forces vectors AP and AB to lie on the same line through A and B. Changing the values of λ will cause AP to stretch or shrink or even point in the opposite direction of AB.
This vector equation forces vectors AP and AB to lie on the same line through A and B. Changing the values of λ will cause AP to stretch or shrink or even point in the opposite direction of AB.

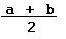
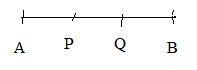 Now consider a point that is 1/3 the way from one end point of a segment to the other end point. Such a point is called a point of trisection of the segment nearest to the first end point. It too has a position vector locating it in terms of the end points of the segment.
Now consider a point that is 1/3 the way from one end point of a segment to the other end point. Such a point is called a point of trisection of the segment nearest to the first end point. It too has a position vector locating it in terms of the end points of the segment.
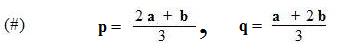
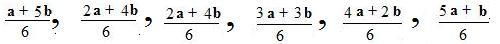
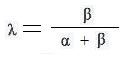
 To answer this question form a triangle using the points A,B,C as vertices. Assume that not all points are one line. Now construct the medians to all three sides: find the mid point A' of side BC, mid point B' of side AC, and mid point C' of side AB. The medians are line segments AA', BB', CC' drawn from the vertices to these mid points. Using the inline notation for position vectors pointing to mid points:
To answer this question form a triangle using the points A,B,C as vertices. Assume that not all points are one line. Now construct the medians to all three sides: find the mid point A' of side BC, mid point B' of side AC, and mid point C' of side AB. The medians are line segments AA', BB', CC' drawn from the vertices to these mid points. Using the inline notation for position vectors pointing to mid points:
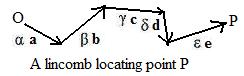 placing the tail of a position vector (term) on the head of the preceding position vector (term). This method of addition produces a direct path from the origin to the head of the final vector (term). That vector locates a point. The entire lincomb locates that same point. In the figure to the right in which copies are made of the terms βb, γc δd, εe, the lincomb
placing the tail of a position vector (term) on the head of the preceding position vector (term). This method of addition produces a direct path from the origin to the head of the final vector (term). That vector locates a point. The entire lincomb locates that same point. In the figure to the right in which copies are made of the terms βb, γc δd, εe, the lincomb