Constructing parallelograms

Given two segments (red and blue) with a common end-point, as shown in Fig 1. (The remaining two end-points will be called free in this discussion.) There are three methods to construct a parallelogram with those segments as sides. All methods locate a point S which will be the fourth vertex of the parallelogram.

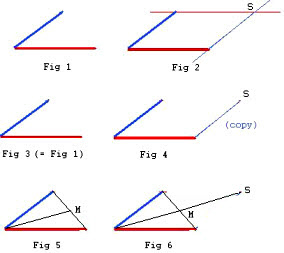The first method uses the basic definition of a parallelogram, namely, that the opposite sides are parallel. Therefore, through the two free end-points construct lines parallel to the opposite segments, as shown in Fig 2. The intersection of these lines locates the fourth point S of the parallelogram.

The second method is a modification of the first method. Copy the blue segment so that the copy and the free end-point of the other red segment are coincident. Then the free end-point of this copy locates the point S as shown in Fig 4.

The third method is based on a theorem of plane geometry. A quadrilateral is a parallelogram if and only if the diagonals bisect each other. Join the free end-points of the given segments and locate its mid-point M. Join the common end-point of the given segments to M, as shown in Fig 5. Extend this segment to a new segment whose mid-point will be M. The free end-point of this new segment is the point S as shown in Fig 6.


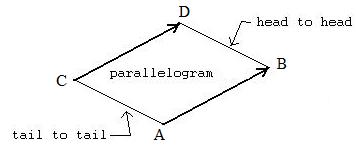
Geometric test for equivalence of two vectors

It requires construction of two parallel lines. Contruct a line through the two heads and another line through the two tails. If a genuine parallelogram is formed then the two vectors are equivalent.

If the vectors are on the same line then construct an image of one of them on a second parallel line (see below). The compare that image with the second vector.


Geometric construction of an equivalent vector

Case I. The vectors are along different parallel lines. Given a vector. And given a point somewhere. Construct an equivalent vector with its tail at the given point. Draw a line through the two tails. This gives us two sides of a parallelogram.. A third side comes from drawing a line through the head of the vector parallel to the line just drawn, and a fourth side from a line drawn through the given point parallel to the vector.

Case II. The vectors are on the same line. Draw a distinct parallel line. Construct an image on this line. From that image construct an image on the original line.


Geometric Drawings Go to other chapters or to other volumes of math
Return to Chapter 1: Geometric Vectors
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises

Geometric Drawings







[1] Given a line and a point, to draw a line through the point and parallel to the given line.


In many constructions involved in discussions in this chapter on geometric vectors, it is necessary to draw a line parallel to a given line. More specifically, to draw a line through a given point and parallel to a given line. One easy way is to use a Tsquare and move the paper so that the edge of the Tsquare is along the given line and fasten the paper down so that it does not move. Then slide the Tsquare up or down until it its edge now is on the point. Then draw a line through the point along the edge.


[2a] Given two intersecting (but distinct) lines and a point on each, distinct from the point of intersection. To draw a parallelogram along the two lines and with the three points as vertices. Tsquare method.

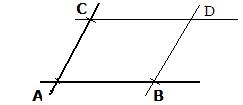Let A be the point of intersection of the two given lines, and B and C be the other given two points. Using the construction given in [1] above, draw a line through B parallel to the line AC. Also draw a line through C parallel to line AB. The intersection D of the two newly drawn lines locates the fourth vertex of the parallelogram.


[2b] Given two intersecting (but distinct) lines and a point on each, distinct from the point of intersection. To draw a parallelogram along the two lines and with the three points as vertices. Diagonal method.

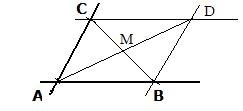This method uses the converse of the theorem that the diagonals of a parallelogram bisect each other. Let A be the point of intersection of the two given lines, and B and C be the other giventwo points. Draw line segment BC. Locate its midpoint M. Draw line AM. Copy segment AM so that the copied segment is along the line and has an end point on M. The other end point locates the fourth vertex D of the parallelogram.

This method does not require the Tsquare, but has more work involved, to get the midpoint M and to construct segment MD. There are other methods of bisecting segments to get the midpoint thn using arcs of circles.


[2c] Given two intersecting (but distinct) lines and a point on each, distinct from the point of intersection. To draw a parallelogram along the two lines and with the three points as vertices. Opposite sides equal method.

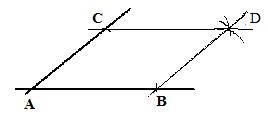This method uses the converse of the theorem that the opposite sides of a parallelogram have equal lengths. It is the most convenient method of constructing the parallelogram.

Let A be the interesection of the two lines, and let B and C be the points on the two lines. Using a compass, with B as center and |AC| as radius, draw an arc in the vicinity of the fourth vertex D of the parallelogram. With C as center and |AB| as radius draw an arc intersecting the other arc. The point of intersection is the fourth vertex D of the parallelogram. Draw segments BD and CD to complete the parallelogram.

A very minor objection to this method is that arcs of circles are not part of affine geometry. But the reader is welcome to use it.


[3] Given a vector and a point. To copy the vector so that the initial point of the vector is copied onto the given point.

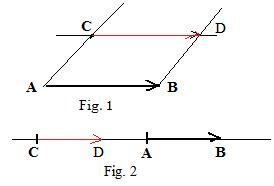Let A and B be the initial and terminal points of the vector, and let C be the point.

Case I: (Fig 1.) C is off the line through A and B. Draw segment AC. Draw a parallelogram with sides AB and AC (see [2] above). Let D be the fourth vertex. Convert segment CD into a vector CD, which is a copy of AB and has its initial point on C.

Case 2: (Fig 2.) C is on the line through A and B. Copy vector AB directly along the line so that the initial point of the copy is on C, and that the vectors AB and the copy have the same lengths and directions along the line. (The vertices of the vectors of AB and the copy should be those of a collapsed parallelogram.)


[4] Given two vectors. To test to see if they are equivalent.

Case 1: The vectors are along different lines. Draw the segment that joins the initial points of the two vectors, and also the segment that joins their terminal points. The vectors are equivalent if and only if the figure forms a parallelogram. (The diagonals should bisect each other.)

Case 2: The vectors are along the same line. Test equality of their lengths, and see if they point in the same direction.


[5] Given two position vectors p and q. To draw their sum p + q using a parallelogram.

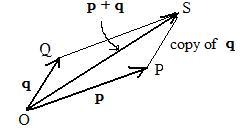Given position vectors p and q. These locate points P and Q. Construct a parallelogram from a line containing vector OP and the point Q located by position vector q. (See [2] above.) A copy of q is made and moved so that its initial point is on the point P. (See [3] above.) The copy is a position vector that locates a new point S, so that PS and q are equivalent vectors. The diagonal vector OS is the desired vector sum   OS = p + q. Also OS is the resultant of the process of obtaining this vector sum.


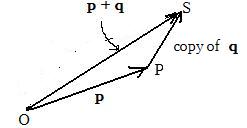
[6] Given two position vectors p and q. To draw their sum p + q using a triangle.

A copy of q (which is not shown) is made and the initial point (tail) of it is placed on the terminal point P (head) of p. The terminal point (head) of the copy locates a point S. The triangle OPS is formed and OS is the resultant:   OS = p + q.


[7] Given a position vector. To draw its negative

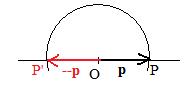Let p be any position vector. It locates a point P. Construct a position vector of the same length as p but pointing in the opposite direction. This can be done by constructing a circle with center at origin O and radius equal to the length |OP| of p. The circle intersects the line containing O and P at P'. Draw the position vector OP' from origin to P'.   --p = OP'.