Return to main page
Additional Material D1
 >
>
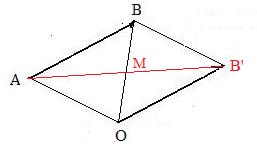
Construction of a parallelogram given two adjacent sides and the included angle
Given points O, A, B which are really vertices of half of the desired parallelogram. Locate the midpoint M of line segment OB. Consstruct a line segment AM and extend it an equal amount to a point B' so that M is the midpoint of AB'. Then B' is the desired point so that B, A, O, B' are vertices of a parallelogram
A position vector cannot have more than one additive inverse
Suppose that q and r are additive inverses of p. Then by definition,
p + q = 0 p + r = 0
Therefore p + q = p + r. Add −p to both sides of this last equation produces q = r.
Product of a number and a position vector
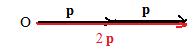 An intuitive discussion about vectors multiplied by numbers. Let p be any position vector. It seems natural that 1p = p. The vector sum p + p of p with itself can be constructed using the triangle method: make a copy of p and put its tail on the head of p. It is natural to call the resultant 2p. In the drawing, 2p is a position vector with the same direction as p but is twice as long. A similar experiment shows that 3p = p + p + p is a position vector with the same direction as p but is three times as long. The following is an inductive generalization:
An intuitive discussion about vectors multiplied by numbers. Let p be any position vector. It seems natural that 1p = p. The vector sum p + p of p with itself can be constructed using the triangle method: make a copy of p and put its tail on the head of p. It is natural to call the resultant 2p. In the drawing, 2p is a position vector with the same direction as p but is twice as long. A similar experiment shows that 3p = p + p + p is a position vector with the same direction as p but is three times as long. The following is an inductive generalization:
[*] (Multiplication of a vector by a positive integer) The product of a positive integer n and a position vector is a position vector that points in the same direction and has a length n times the length of the original vector.
Notation: For any positive integer n, np = p + p + ... + p (n appearances of p) is a position vector pointing in the same direction as p and having a length n times as long as p.
Multiplication of a vector by an integer larger than 1 causes the vector to become longer.
If segment OP is bisected to locate a point Q then a segment OQ half as long as OP is produced. Then q = (1/2)p. Similarly if segment OP is trisected to locate a point R nearest the origin, then segment OR is (1/3)OP and therefore r = (1/3)p. In general, OP can be divided into n congruent parts, locating a point T nearest the origin. Therefore, t = (1/n)p. Once that a position vector can be divided into n congruent parts,then the product (1/n) and the position vector is defined. If m is any positive integer, then (m/n)p can be defined as
(m/n)p = (1/n)p + (1/n)p + . . . + (1/n)p (m appearances of (1/n)p)
[**] (Multiplication of a vector by a positive rational number) The product of a positive fraction and a position vector is a position vector that points in the same direction and has length which is the fraction times the length of the original vector.
Notation: For the product (m/n)p, it points in the same direction as p and its length |(m/n)p| = (m/n)|p|.
Intuitive discussions supporting the distributive laws for multiplication of positive integers and position vectors
[*] (Right distributive law for multiplication by positive integers) Let m and n be any positive integers. Then if the resultant of m copies of a position vector added to gether, are added to the resultant of n copies of that same vector added together, then the sum of the two resultants is the same as the resultant of m + n copies of that vector added together.
Notation: (m + n)p = mp + np.
This law is a simple use of counting.
(m + n)p = p + p + . . . + p [(m + n) appearances of p]
= p + p + . . . + p + [m appearances of p]
= p + p + . . . + p [n appearances of p]
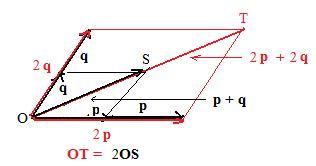 The previous discussion involved two numbers and one vector. Now consider one number and two vectors. From simple algebra, 2(p + q) = (p + q) + (p + q) = p + q + p + q = 2p + 2q. The adjacent figure supports geometrically through similarity the statement 2(p + q) = 2p + 2q. The red parallelogram is twice as big as the black parallelogram. The equality 3(p + q) = 3p + 3q can be proved by algebra and by another figure of similar parallelograms where the red parallelogram is three times as big as the black parallelogram. This process continues on inductively through all the integers and supports the following statement:
The previous discussion involved two numbers and one vector. Now consider one number and two vectors. From simple algebra, 2(p + q) = (p + q) + (p + q) = p + q + p + q = 2p + 2q. The adjacent figure supports geometrically through similarity the statement 2(p + q) = 2p + 2q. The red parallelogram is twice as big as the black parallelogram. The equality 3(p + q) = 3p + 3q can be proved by algebra and by another figure of similar parallelograms where the red parallelogram is three times as big as the black parallelogram. This process continues on inductively through all the integers and supports the following statement:
[**] (Left distributive law for multiplication by positive integers) Let n be any positive integer. The resultant of adding n sums of two position vectors together is equal to the sum of the resultants of adding each vector to itself n times.
Notation: n(p + q) = np + nq.
The following supporting discussion is more algebraic in nature and use the associative and commutative laws for vectors with addition.
n(p + q) = (p + q) + (p + q) + ... + (p + q) [n appearances of (p + q)]
= p + p + . . . p + q + q + . . . + q [n appearances of p and n appearances of q]
= np + nq.
Geometric argument supporting the distributive law λ(p +q) = λp + λq
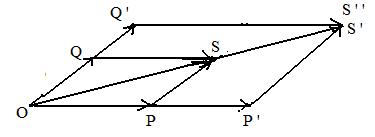 In the adjacent figure, P and Q are the points located by position vectors p,q:
In the adjacent figure, P and Q are the points located by position vectors p,q:
OP = p, OQ = q.
Let S be the point located by a vector sum:
OS = OP + OQ = p + q
Let P' and Q' be points such that
OP' = λOP = λp
and
OQ' = λOQ = λq.
Construct a line through point P' and parallel to line PS. Let S' be the intersection of this new line and the diagonal line OS.
Then triangles OPS and OP'S' are similar. Therefore,
|OS'|/|OS| = |OP'|/|OP| = λ
So |OS'| = λ|OS|
Draw a line through Q' parallel to line QS. Let S" be the intersection of this new line and the diagonal line OS.
Then triangles OQS and OQ'S" are similar. Therefore, \
|OS"|/|OS| = |OQ'|/|OQ| = λ
So |OS"| = λ|OS| and S" = S'.
Then the opposite sides of quadrilateral OP'S'Q' are parallel so OP'S'Q' is a parallelogram. Then the opposites have the same lengths and
it is the addition parallelogram for the vector sum
OS' = OP' + OQ'
Therefore, λ(p + q) = λ(OP + OQ) = λOS = OS' = OP' + OQ' = λOP + λOQ = λp + λq.
Position vectors in space
Here "space" means 3-dimentional space of high school solid geometry.
[PVS.1] Some theorems (and definitions) borrowed from solid geometry may be used for vectors in space:
(a) Three non-collinear points locate a unique plane.
(b) A line and a plane either intersect in a point or are parallel.
(c) If two distinct points on a line are also in a plane then the entire line is in the plane.
(d) Two distinct and parallel lines locate a unique plane.
(e) Two distinct and intersecting lines locate a unique plane.
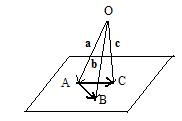
In Section 1 of the main page, it was stated that in any discussion about position vectors there is always some point O called the origin. There was no condition imposed on the location of O. Although drawings there suggested that the origin and all points under discussion lie in the same plane, everything discussed there remains true when the origin is not in the same plane as the points. The adjacent figure shows points A,B,C in a plane but the origin O is not in that plane. Nevertheless, position vectors a,b,c joining the origin to the points exist in space and obey all the equations and statements made in Section 1. For example
the simple equation AB = b − a, mid point equation 2m = a + b and the centroid equation for triangle ABC 3g = a + b + c
are still true, for any location of the origin.
In Section 1 the condition that a point P lies on a line through distinct points A,B was given: that there exist scalars α and β whose sum is not zero and
(*) (α + β)p = αa + βb
There is a similar condition that forces a point P to lie in the plane of points A,B,C
[PVS.2] Point P lies in the plane of non-collinear points A,B,C if and only if there exist scalars α, β and γ whose sum is not zero such that
(**) (α + β + γ)p = αa + βb + γc
There are the usual two implication parts of the equivalence.
(==>) Given that P lies in plane of non-collinear points A,B,C.
Pass lines through points A and B and through points C and P. By [PVS.1e] those lines are in the same plane (and cannot be skew). There are two situations: the two lines AB and CP intersect or are parallel.
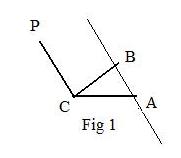 Situation1: Lines CP and AB are parallel (Fig 1).
Situation1: Lines CP and AB are parallel (Fig 1).
Then vector CP is proportional to vector AB. There exists a scalar λ satisfying
CP = λAB
Then position vectors
p − c = λb − a
Use simple algebra to get
p = −λa + λb + c
Choose α = −λ, β = λ, γ = 1 to get equation (**).
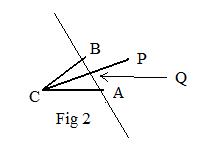 Situation2: Lines CP and AB intersect (Fig 2).
Situation2: Lines CP and AB intersect (Fig 2).
Let Q be the point of intersection CP∩AB.
Q is on line CP. Then vectors CQ and CP are parallel and hence proportional:
There exists a scalar λ satisfying
CQ = λCP.
Then
q − c = λp − λc.
or
(#) q = λp + (1 − λ)c.
Q is on line AB. Then by (*) above, using q in place of p, for some scalars α and β:
(##) (α + β)q = αa + βb
Eliminate q in (#) and (##) by substitution and solve for the term λ(α + β)p to get:
(###) λ(α + β)p = αa + βb + (λ − 1)(α + β)c.
Let γ = (λ − 1)(α + β).
Then simple algebra shows that:
λ(α + β) = α + β + γ.
Substitution of these two scalar expressions into (###) produces equation (**).
...
The above has shown that if P is in the plane of non-collinear points A,B,C then (**) is true.
(<==) Conversely if (**) is true then P is in the plane of A,B,C. To show this, there are two cases, α + β = 0 and α + β ≠ 0.
Case I: α + β = 0.
 Then β = − α. Also, γ ≠ 0.
Then β = − α. Also, γ ≠ 0.
Also, γp = αa − αb + γc.
γ(p − c) = α(a − b
γCP = αBA
CP = (α/γ)BA
CP || BA. (Fig 1)
These lines are distinct because A,B,C are not collinear.
By [PVS.1d], those lines, CP and BA, locate a single plane.
A,B,C,P all lie in the same plane.
Point P lies in plane A,B,C.
Case II: α + β ≠ 0.
 Subtract γc from both sides of (**) to get an equation in scalar balance:
Subtract γc from both sides of (**) to get an equation in scalar balance:
(α + β + γ)p − γc = αa + βb.
Let (α + β)q = each side of this equation. Then Q is on the intersection PC∩AB.
Points A,B,C lie in the plane of these intersecting lines PC and AB. (Fig 2)
Since A,B,C are not collinear they determine a single plane ABC.
By [PVS.1e] the plane of intersecting lines must coincide with plane ABC.
Therefore P lies in plane ABC.
 The previous discussion involved two numbers and one vector. Now consider one number and two vectors. From simple algebra, 2(p + q) = (p + q) + (p + q) = p + q + p + q = 2p + 2q. The adjacent figure supports geometrically through similarity the statement 2(p + q) = 2p + 2q. The red parallelogram is twice as big as the black parallelogram. The equality 3(p + q) = 3p + 3q can be proved by algebra and by another figure of similar parallelograms where the red parallelogram is three times as big as the black parallelogram. This process continues on inductively through all the integers and supports the following statement:
The previous discussion involved two numbers and one vector. Now consider one number and two vectors. From simple algebra, 2(p + q) = (p + q) + (p + q) = p + q + p + q = 2p + 2q. The adjacent figure supports geometrically through similarity the statement 2(p + q) = 2p + 2q. The red parallelogram is twice as big as the black parallelogram. The equality 3(p + q) = 3p + 3q can be proved by algebra and by another figure of similar parallelograms where the red parallelogram is three times as big as the black parallelogram. This process continues on inductively through all the integers and supports the following statement:
 >
>
 An intuitive discussion about vectors multiplied by numbers. Let p be any position vector. It seems natural that 1p = p. The vector sum p + p of p with itself can be constructed using the triangle method: make a copy of p and put its tail on the head of p. It is natural to call the resultant 2p. In the drawing, 2p is a position vector with the same direction as p but is twice as long. A similar experiment shows that 3p = p + p + p is a position vector with the same direction as p but is three times as long. The following is an inductive generalization:
An intuitive discussion about vectors multiplied by numbers. Let p be any position vector. It seems natural that 1p = p. The vector sum p + p of p with itself can be constructed using the triangle method: make a copy of p and put its tail on the head of p. It is natural to call the resultant 2p. In the drawing, 2p is a position vector with the same direction as p but is twice as long. A similar experiment shows that 3p = p + p + p is a position vector with the same direction as p but is three times as long. The following is an inductive generalization:
 In the adjacent figure, P and Q are the points located by position vectors p,q:
In the adjacent figure, P and Q are the points located by position vectors p,q:
 Situation1: Lines CP and AB are parallel (Fig 1).
Situation1: Lines CP and AB are parallel (Fig 1).
 Situation2: Lines CP and AB intersect (Fig 2).
Situation2: Lines CP and AB intersect (Fig 2).