Return to main page
.

Additional Material




Sum of even numbers is even

Let x,y be even numbers. Then they must be doubles. Let x=2u and y=2v. Then x+y = 2u+2v = 2(u+v). So their sum is a double, and therefore the sum must be even.


Any object in a group is equal to the inverse of its inverse.

To show the reverse identity (x-1)-1 = x.
For any object w, wow-1 = e.    This is also true for w = x-1.
Then wow-1 = e ==>
   xowow-1 = xoe ==>
   xowow-1 = x ==>
   xox-1o(x-1)-1 = x ==>
   eo(x-1)-1 = x ==>
   (x-1)-1 = x.


Some computations for the table of multiplications

Use will be made of the following identities that define the non-commutative group of six objects:
ba = a2b,      ba2 = ab,      a3 = e,      b2 = e

aba = aba = aa2b = aa2b = eb = b.
aba2 = aba2 = aab = aab = a2b = a2b.
abab = abab = aa2bb = aa2bb = a3b2 = ee = e.
aba2b = aba2b = aabb = aabb = a2b2 = a2e = a2.
a2ba = a2ba = a2a2b = a2a2b = a4b = a3ab = eab = ab = ab.
a2bab = a2bab = a2a2bb = a2a2bb = a4e = a
a2ba2 = ... = ... = b
a2ba2b = ... = ... = e

Last two equalities left as exercises.


xy-1 determines a subgroup

If H is a subset of a group G, and for all x,y in H, xy-1 is back in H, then H is a subgroup of G.

Since y can be anything in H, y=x is possible. So e = xx-1 = xy-1 is in H. Therefore H has the identity.
x can be anything in H, so x=e is possible. Then for any y in H, y-1 = ey-1 = xy-1 is in H. therefore every object in H has its inverse back in H.
Let z = y-1.   Then z-1 = (y-1)-1 = y. For every x,z in H, xy = xz-1 is in H. (Closure).


Parallel lines as cosets

It is possible to combine two subsets of a group and form a new subset. For example, let
S1 = {1,3,6}   and   S2 = {4,8} as subsets of the additive integers J
Then the sum   S1 + S2 is a subset of J, formed by taking sums of every number in the first subset with every number in the seconds subset:
S1 + S2 = {1+4, 1+8, 3+4, 3+8, 6+4, 6+8} = {5,7,9,10,11,14}
If one of the subsets has only one object in it, then the curly brackets are obmitted:
2 + S1 = {2+1, 2+3, 2+6} = {3,5,8}
Because addition is commutative,   S1 + S2 = S2 + S1   and   2 + S = S + 2.
Now let G = {e, a, a2, b, ab, a2b}. be the non-commutative group discussed in [1.5]. Let S = {e,a}. Then
bS = {b, ba} = {b, a2b}    and    Sb = {b, ab}.
But sets   bS ≠ Sb   because   a2b ≠ ab.
If S = {e, a, a2}   then bS = Sb. Therefore, in a non-commutative group, multiplying a subset on the left by an object may or may not be the same as multiplying the subset on the right.

if e is the identity, then   eS = S, because when the product of e and each object in S is that same object.
Let H be a subgroup. And let h be any object in H. Then   hH = H   because multiplying all the objects in H by h merely rearranges the objects in H. Also, HH = H.
If w is any object in G, then wH is called a left coset of H and Hw is called a right coset of H. As pointed out above, in a non-commutative group a left coset and a right coset of a subgroup may or may not be the same.

A subgroup of a group is a normal subgroup if every left coset of the subgroup is equal to the corresponding right coset.
Notation: Let H be a subgroup of a group G. H is normal if and only if for every object x in G, xH = Hx.

Example1. Let G be the non-commutative group of six objects. Let H = {e, a, a2}. Then bH = {b, a2b, ab} = Hb. The reader can verify that abH = Hab and a2b = H a2b. (Why is it not necessary to test cosets with multiplication with e,a, a2? Therefore xH = Hx and H is normal.

Exmple2. This time let H = {e, b}. The reader can verify that aH ≠ Ha. So H is not a normal subset.

==================

If there is a binary operation, then it is possible to combine a object with a subset of objects to get a subset.. Let subset S = {a,b,c,d} and let w be any object in the set. Then

wS = {wa, wb, wc, wd}    and    Sw = {aw, bw, cw, dw}
If the binary operation is addition, then
w+S = {w+a, w+b, w+c, w+d}    and    S+w = {a+w, b+w, c+w, d+w}
But addition operator is always commutative, so   w+a = a+w,   w+b = b+w,   w+c=c+w,   w+d=d+w.   Therefore   w+S = S+w.

In most discussions the set will be a group and the subset will be a subgroup. In [2.3] an additive group structure was imposed on the coordinate plane. Any line W through the origin is an additive subgroup of the plane. If W is the y-axis, then a point is in W if and only if its x-coordinate is zero. Let (0,u) and (0,v) be points in W. then

(0,u) – (0,v) = (0,u-v)
shows that W is closed using subtraction. By [3.2] W is a subgroup of the plane.
Suppose the line is any line through the origin not the y-axis. Then it has a slope   m.   W has an equation   y = mx.   Suppose (x,y) and (x',y') are points on W. Then   y = mx   y' = mx'. Hence y - y' = m(x - x'). So (x-x',y-y') is on W. Therefore, the difference of any points on W is on W. By [3.2] W is a subgroup of the plane.

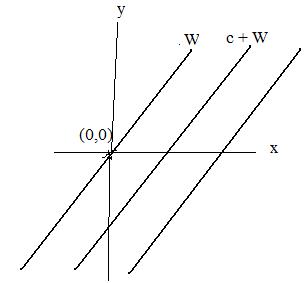Let   c   be any real number. Add   c   to every point (x,y) on W to get a new point (x + c, y + c). (If W is the y-axis then add   c   to every point (0,y) on W.) If the W has slope   m   then the equation of W is   y = mx.   After adding   c   to every point of W, the new line has equation y = mx – c. (Click here to see why this is so.) (If W is the y-axis, then x = c is the new line.) The new line, denoted by   c + W   is parallel to W because both lines have the same slope. (If W = y-axis then W and c + W are vertical lines.) As c changes values, a family of parallel lines is produced. (In fact as c assumes all real numbers, a partition of the coordinate plane is formed from all these parallel lines.) Each of these lines parallel to W is called a coset of W. The coset   c + W   is not a subgroup.

It is possible to impose a "natural" addition operation on all these cosets of parallel lines:

for   c + W   and   d + W   their sum is   (c + d) + W.
It can be proven that this addition of cosets is associative.
The coset   W = 0 + W   is the additive identity.
The coset   -c + W   is the additive inverse of the coset   c + W
Therefore all the cosets of W (that includes W) is an additive group, called the factor group of W. If U is the coordinate plane, then U/W denotes this group.


Cosets of a subgroup H form a partition of the main group G

Recall that the equivalence classes of an equivalence relation on a set form a partition of that set. The idea here is to introduce an equivalence relation on group G and then show that the left cosets of H coincide with the equivalence classes of the relation.

Define a relation ~ on G as follows:    x ~ y   if and only if   x-1y is in H,    where x and y are any objects in G.

Part I:   First show that ~ is an equivalence relation.
(a) ~ is reflexive   x ~ x   because   x-1x = e   and   identity e is in subgroup H.
(b) ~ is symmetric   x ~ y   ==>   x-1y is in H   ==>   y-1x is in H   ==>   y ~ x.
       Note about implication ==>: the inverse of   x-1y   is y-1x   because their product = e.    H contains inverses of all its objects.
(c) ~ is transitive   x ~ y and y ~ z   ==>   x-1y is in H and y-1z is in H   ==>   (x-1y)(y-1z)   ==>   x-1z is in H   ==>   x ~ z
       Note about implication ==>: H is closed under multiplication.

Part II:   Next show that   the equivalence classes of ~   coincide with   the left cosets of H
x is in [y]   <==>   x ~ y       [definition of equivalence class [y]
                <==>   x-1y is in H       [definition of ~]
                <==>   y-1x is in H       [H contains all inverses of its objects]
                <==>   y-1x = h    for some h in H
                <==>   x = yh
                <==>   x is in yH

Therefore, [y] = yH.   This is true for all y in G. Therefore, the equivalence classes of ~ coincide with the left cosets of H. Hence the left cosets form a partition of G because equivalence classes do that.