[1.1] (Binary operations) A binary operation on a set combines every pair of objects in the set to produce a third object.
Notation: Let o denote a binary operation of a set U. Then any pair of objects x,y, xoy is an object in U by combining x and y.
The operation produces a single object, never more than one object from any pair of objects. (The operation is said to be single valued.)
The third object xoy may or may not be different from the objects in the pair x,y. The objects x,y in the pair may be different or may be equal.
The objects x and y may be anywhere in some subset S of set U. Where the binary operation o places the third object x o y is important: inside S or outside in U\S. Let S = {1, 2, 3}. Then S is a subset of the natural numbers N. The sums are back in S for some pairs of numbers in S. For example 1 + 1, 2 + 1, 1 + 2. But other sums are outside S. For example 2 + 3, 3 + 3.
[1.2] (Closure) A binary operation is closed on a subset if, for all pairs of objects in that subset, the operation combines the pair and produces a third object in that same subset.
Notation: For closure of operation o on subset S, for every pair of objects x,y in S, x o y is always in S.
Example: The operation of multiplication on the subset
A binary operation not closed on a subset severely limits the algebraic use of that subset. It will always be assumed that a binary operation on a universe U is always closed on the universe. Since division by zero is not allowed, the operation of division is not closed on the set of all real numbers. To be useful, the universe may become the real numbers without zero in discussions about division.
-----
It is sometimes useful to extend the binary operation on a set to a similar operation involving subsets in tht set.
[1.3] (Operations on subsets) To combine two subsets of a set with a binary operation defined on it, form a set of all combinings of objects, the first taken from the first subset and the second taken from the second subset.
Notation: Let S1 and S2 be subsets of a set U with a binary operation o on it. Then the combining of the two subsets S1 o S2 is obtained by forming a single subset of all combinings s1 o s2 where s1 is any object in S1 and s2 is any object in S2.
The binary operation on U is said to induce a similar operation on the family (power set) of all subsets of U.
Notation: x is in S1 o S2 if and only if there are objects s1 in S1 and s2 in S2 such that x = s1 o s2.
Examples
It is possible that some of the combinings are equal: 1+4 = 2+3, so {1,2} + {3,4} = {4, 5, 5, 6} = {4, 5, 6}.
It is possible that either subset in S1 o S2 has only one object in it. Then the curly braces {} around it are omitted:
Examples:
The following is obvious but will be useful in some discussions in Section 6 below.
[1.4] (Condition for an object to be in aoS) Let S be any subset. For an object x to be in aoS, the object x = aos for some object s in S.
[1.5] (Binary operations are single-valued) From any objects x and y, a binary operation produces a single object x o y, , that is, x o y cannot equal two or more different objects for the same pair x and y.
(1a) The sum of real numbers is a real number.
(1m) the product of real numbers is a real number.
(2a) Addition is associative: x + (y + z) = (x + y) + z.
(2m) Multiplication is associative: x(yz) = (xy)z.
(3a) There is an additive identity 0 such that x + 0 = x = 0 + x.
(3m) There is a multiplicative identity 1 such that x1 = x = 1x.
(4a) Each real number x has an additive inverse -x satisfying x + (-x) = 0 = -x + x.
(4m) Each non-zero real number x has a multiplicative inverse 1/x satisfying x(1/x) = 1 = (1/x)x.
There are four similar statements about the addition and multiplication of complex numbers and similar statements about the addition and multiplication of quaternions.
The permutations (and in general one-to-one functions between a non-empty set and itself) also have similar properties:
(1p) The product of permutations (on the same collection) is a permutation.
(2p) Multiplication is associative: f(gh) = (fg)h.
(3p) There is an identity permutation I satisfying fI = f and If = f.
(4p) Each permutation f has an inverse permutation f-1 so that ff-1 = I and f-1f = I.
A glaring omission in the above examples is the commutative law. This omission allows permutations and quaternions to be included in this discussion. It is customary to consider systems with addition to be commutative. Systems with multiplication may or may not be commutative.
In any case there is involved an operation that combines any two objects and produces a third object. This is called a binary operation. Addition and multiplication of numbers are binary operations. Product of permutations and in general functions involve binary operations.
Here o denotes a binary operation in general, and xoy is called a product. If o is replaced by the addition symbol + then replace xoy by x+y and the word "product " by the word "sum" and any inverse x-1 by the additive inverse -x. Also the identity e is replaced by zero 0 for addition and one 1 for multiplication of numbers. For functions and permutations replace e by I.
In all of these volumes, every binary operation is associative.
For many algebraic systems to be useful, mathematicians have decided that four conditions must be satisfied.
[2.1] (Groups) A set of objects forms a group if there is a binary operation o satisfying the following conditions:
(a)(closure) The operation on any pair of objects x,y in the set produces a unique object xoy in the set.
(b)(associative) The operation is associative: xo(yoz) = (xoy)oz, for any objects x,y,z in the set.
(c)(identity) There is an identity object e in the set such that xoe = x and eox = x, for every object x in the set.
(d)(inverse) Each object x has an inverse object x-1 in the set, satisfying x o x-1 = e and x-1 o x = e.
Strictly speaking, the operation is as much a part of the group as any object in the set. If the set is G, then G o is the group. But very often the operation is known and it will be said simply that G is a group.
Intuitively speaking, a group has a minimum number of conditions to do work in algebra. For example, it can solve simple equations line a o x = b, where a and b are known quantities, and x is the unknown.
However, often the operation symbol o is omitted if the operation is not addition. Then xy is called the product of x and y.
It is instructive to see a system that is not a group. In this example, the operation fails to have closure [2.1a]. The system of odd natural numbers, 1,3,5,7,9, ... is not closed with respect to addition. The sum of any pair is not an odd natural number:
The natural numbers N are are closed under addition but do not have the identity zero, nor the negative additive inverses. The expansion of N to the system J of integers produced a group J +. The integers, in turn, are not a group under multiplication. The integers were expanded to the system of rational numbers. Without zero the rational numbers form a multiplicative group. When a smaller number system was not a group (intuitively speaking, "defective") a larger system was invented to be a group.
Many systems satisfy the conditions for a group. Instead of developing and proving very similar statements about each new system, it is more economical to present these statements and proofs here that are true for all groups. Most are simple but may involve ideas that are new to the reader.
[2.2] (Unique identity) A group has only one object that is the identity.
Notation: if both e and e' are identities in the same group then e = e'.
Sometimes equality is achieved by evaluating some expression two different ways. In this case the expression is the product ee'. One evaluation uses e as an identity on the left. The other uses e' as an identity on the right
Since e is an identity, then eox = x is true for all objects x in the group, including x=e': eoe' = e'
Since e' is an identity, then yoe' = y is true for all objects y in the group, including y=e: eoe' = e
Therefore, both e and e' are equal to eoe' and hence equal to each other: e = e'.
[2.3] (Unique inverse) For any object in a group there is only one inverse.
Notation: if both w and w' are inverses of x then w = w'.
The following facts are needed: the product of an object and an inverse equals the identity. Also the product of an inverse and the object equals the identity.
Let both w and w' be inverses of object y. Then evaluate wyw' two ways.
Since w is an inverse of y, wyw' = (wy)w' = ew' = w'.
Since w' is an inverse of y, wxw' = w(yw') = we = w.
Therefore, both w and w' are equal to wyw'. Hence they are equal: w = w'.
[2.4] (Inverse of an inverse) Every object in a group is equal to the inverse of its inverse.
Notation: x = (x-1)-1.
The argument here proves (y-1)-1 = y. The idea is to show both y and (y-1)-1 are inverses of y-1 and then apply [1.3].
Let w be the inverse of y: w = y-1. Then wy = e. So y is the inverse of w.
But w-1 is also the inverse of w.
But by [2.3] w can have only one inverse. Therefore y = w-1 = (y-1)-1.
[3.1] (Additive integers) The most familiar commutative group is the additive integers J = {..., -2, -1, 0, 1, 2, ...}. Under multiplication J is not a group.
[3.2] (Integers mod n) For any natural number n, the set Jn = {0,1,2,...,n-1} using addition mod n forms a commutative group. If n is a prime natural number then the non-negative numbers in Jn form a commutative multiplicative group. Click here to see a discussion of this statement.
[3.3] (Points in the coordinate plane) It is easy to impose a binary operation of addition on the plane of elementary algebra. If (x,y) and (x',y') are points then their sum is (x + x', y + y'). The origin (0,0) is the identity. (-x,-y) is the additive inverse of (x,y). Volume D will give more details of this algebraic system.
[3.4] The symmetries of an equilateral triangle and permutations.
The six permutations of 1,2,3 can be described by motions of an equilateral triangle. The objects are the vertices of this triangle. They will be three fixed but equally distant points, instead of blanks. These points have location numbers 1,2,3 assigned in a counter-clockwise direction. Any segment joining 1 and 2 would be horizontal. There is an invisible line through 3 and perpendicular to the horizontal line. When not in motion the triangle sits with its vertices on the three fixed points When in motion the triangle is not distorted, changes shape nor is bent.
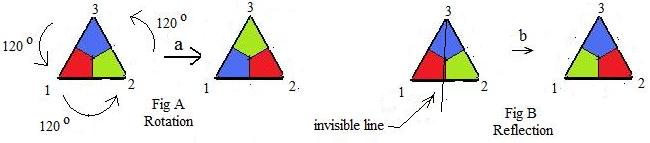There will be three fundamental motions of the triangle so that its vertices will be on the three fixed points before and after the motions (the vertices have been colored):
(a) rotation counterclockwise through 120° about the center of the triangle (Fig A),
(b) flipping the triangle over and about the invisible line, vertex at 3 stays fixed (Fig B),
(e) no movement.
The rotation in fig A changes the arrangement of the vertices on the fixed points. The vertex that was at point with location number 1 has been moved onto point with location number 2, the vertex that was at the point with location number 2 has been moved onto point with location number 3, and the vertex that was at the point with location number 3 has been moved onto the point with location number 1. This rotation motion through 120° is given a label a:
a: 1 → 2, , 2 → 3, 3 → 1
The reflection in Fig B means an interchange of vertices at locations 1 and 2 (1 <→ 2) but the vertex at 3 does not change location. This motion is given a label b:
b: 1 → 2, 2 → 1, 3 → 3
The absence of motion means that every vertex is fixed. This lack of motion is called e:
b: 1 → 1, 2 → 2, 3 → 3
It is obvious that e = I, the identity.
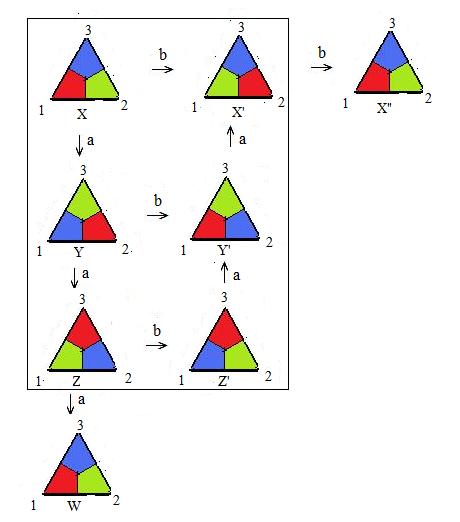The rotation a and reflection b may be applied to any triangle with vertices on the fixed points. In the adjacent figure, a rotates arrangement X through 120° to produce arrangement Y. Denote this action by
ab: X → Y → Y'
a2b: X → Z → Z'.
All six permutations have been mentioned. By seeing what the permutations change X into, it is possible to derive the permutations of location numbers:
e: 1 → 1, 2 → 2, 3 → 3; [equivalent to no motion]
a: 1 → 2, 2 → 3, 3 → 1; [X → Y]
a2: 1 → 3, 2 → 1, 3 → 2; [X → Z]
b: 1 → 2, 2 → 1, 3 → 3; [X → X']
ab: 1 → 1, 2 → 3, 3 → 2; [X → Y']
a2b: 1 → 3, 2 → 2; 3 → 1; [X → Z']
a3 = e, b2 = e.
All the 6 permuttions have been found. They form a group. Product of any two permutations in the group is a permutation in the group. Then what is ba ? There is no path from X to X' and then down. But ba can be computed as a product of two functions:
[3.5] (Multiplication table for the non-commutative group of six objects)
Objects in the left column multiply objects in the top row.
The entries inside the table are in alphabetical order, no b comes before an a. . Although the permutations of the triangle can be used to construct the table or verify some of its contents, the table will exist from now on by itself. In connection with this, click here to see some of the calculations that simplify expressions like bab, a2ba2b, etc. They use ba = a2b, ba2 = ab, a3 = e and b2 = e to do this.
Click here for a discussion and exercise of symmetries of a square.
[4.1] (Subgroups) A subgroup of a group satisfies two conditions:
(a) all of its objects form a subset of the main group;
(b) it satisfies three conditions of a group [2.1a], [2.1c], [2.1d] using the same operation o as the main group.
There are always trivial subgroups, namely the subgroup {e} consisting only of an identity, and the whole group itself. They are the smallest and largest subgroups of a given group. But as subgroups these two trivial subgroups are usually not very interesting.
Sometimes it is necessary to show that part of a group is actually a subgroup. One way is to use definition [3.1] directly. The following provides another way that is more algebraic:
[4.2] A subset of a group is a subgroup if and only if the product of every object in the subset and the inverse of every object in the subset is back in the subset.
A subset S is a subgroup of an additive group G + if and only if for every pair of objects x,y in S, x – y is back in S. Then it is said that S is closed under subtraction.
Click here to see the argument supporting [4.2].
Click here to see a discussion of normal subgroups and cosets.
[5.1] (Presrving operations) Suppose S1 and S2 are sets with binary operators o and *. Then, if x and y are objects in S1 they can be combined to form an object xoy in S1. Similarly, if u and v are objects in S2 they can be combined to form an object u*v in S2. A function f: S1 → S2 preserves operations if and only if
Sometimes operations o and * are different. Define h: J → J by h(x) = 3x. Then
[5.2] (Homomorphisms) A function that preserves operations is called a homomorphism.
In most discussions here homomorphisms involve groups.The following says that the image of a group is a group.
[5.4a] (Carry identities onto identities) If e is the identity of G, then f(e) is the identity in Y.
Let e be the identity in G, and let e' = f(e). To show that e' acts like an identity in Y: ye' = y and e'y = y for any y in Y.
[5.4b] (Carry inverses onto inverses) If x-1 is the inverse of x in G, then f(x-1) is the inverse of f(x) in Y.
By definition of inverse xx-1 = e x-1x = e. Apply homorphism f to both sides of these equations to get
An compact equivalent expression for [4.3b] is: f(x-1) = f(x)-1.
The following statement is another way of expressing [5.3].
[5.5] A homomorphism carries subgroups onto subgroups.
A homomorphism from a group to itself is sometimes called an endomorphism, but the term will not be used in discussions here.
[5.6] (Isomorphisms) An isomorphism is a homomorphism that is s one-to-one correspondence between groups. If an isomorphism exists between groups then the groups are said to be isomorphic.
Examples. In [1.5] the rotations of the equilateral triangle were e, a, a2. The rotation a3 rotated the triangle 360° and was equivalent to the identity e. The integers J3 = {0,1,2} mod 3 also have three objects. The one-to-one correspondence f
[6.1] (Cosets) If H denotes a subgroup of G and a is any object in G, then aH is called a left coset of H. In these discussions a is called the coefficient before the subgroup H. There is a similar for discussion for Ha which is called a right coset of H. The object a is called the coefficient after the subgroup H.
[6.2] (Some simple facts about cosets) Let H be any subgroup of a group G.
(a) If the coefficient before the subgroup is in that subgroup, then the left coset is equal to the subgroup.
(b) Every left coset contains the object that is the left coefficient before the subgroup.
(c) Any object x in G is in the left coset cH if and only if c-1x is in H.
[6.3] (Disjoint covering by left cosets) The collection of all left cosets of any subgroup of a group forms a partition of the group.
Click here to see a discussion supporting this theorem.
[6.4] (Lemma) All left cosets of the same subgroup have the same number of objects in them.
It is easier to show that cH and dH have the same number of objects as in H. The function h → ch is one-to-one because
[6.5] (Size of subgroups) The number of objects in a subgroup of a finite group must divide completely into the number of objects in the entire group.
If there are m objects in subgroup H, then by the lemma there are m objects in every left coset of H. There are a finite number of left cosets, because each coset must contain only objects in G. Let k be the number of distinct cosets. Then mk = n. Therefore, m | n.
The statement [6.5], called Lagrange's theorem, tells what subsets cannot be subgroups of a group. For example, there are no subgroups of 5 objects in a group of 12 objects, because 5 is not a factor of 12.
The set H = {e, b} is a subgroup of the non-commutative group G = {e, a, a2, b, ab, a2b}. H has left cosets
[6.6] (Normal subgroups) A subgroup of a group is a normal subgroup if every left coset of the subgroup is equal to the corresponding right coset.
Example1. Any subset of a commutative group is normal.
Example2. Let G be the non-commutative group of six objects. This time let H = {e, a, a2}. Then bH = {b, a2b, ab} = Hb. The reader can verify that
The following is true for any subgroup, normal or not normal.
Lemma1 The combining of any subgroup with itself is equal to the subgroup.
The supporting argument is in two parts.
Part I HH ⊆ H
Part II H ⊆ HH
The following shows that the computation of the combining of left cosets of a subgroup is greatly simplified if the subgroup is normal.
Lemma2 The product of any pair of left cosets of a normal subgroup is equal to the left coset whose coefficient is the product of the coefficients of the pair of left cosets.
x is in (aH)(bH) <==>
The following is a major property of normal subgroups.
[6.8] (Group of cosets) If a subgroup of a group is normal then all its left cosets form a group.
(a) Lemma2 shows closure.
Since f is onto all of Y, there must be an x in G such that f(x) = y. But xe = x and ex = x. Since f is a homomorphism,
-----
A function from a group to a group may be a homomorphism and a one-to-one correspondence:
f(0 + 1) = f(1) = a = ea = f(0)f(1)
f(0 + 2) = f(2) = a2 = ea2 = f(0)f(2)
f(1 + 1) = f(2) = a2 aa = f(1)f(1)
f(1 + 2) = f(3) = a3 = aa2 = f(1)f(2)
f(2 + 2) = f(4) = a4 = aa3 = ae = f(1) = f(2 + 2)
Section 6: Cosets and normal subgroups (optional)
In section 1 above the combination of an object and a subset were combined to form a (new) subset such as a o S. A more useful situation occurs if the subset is actually a subgroup.
There is always a coefficient. Even H alone is a coset and has a coefficient because H = eH, where e is the identity in H and G.
Notation: if h is in subgroup H, then hH = H.
The proof is trivial. The identity e is in H, and h = he, for any object in H. But he has the form of something in hH. So h is in hH by [1.4].
Notation: for any object x in G, x is in xH.
If e is the identity in G and H, then x = xe. But xe is of the form xh, so x is in xH (by [1.3]).
x is in cH <==> x = ch for some h in H <==> c-1x = h <==> c-1x is in H.
Notation: Left cosets cH and dH have the same number of objects in them.
Notation: If n is the number of objects in a group G, and m is the number of objects in a subgroup H, then m is a factor of n.
Notation: Let H be a subgroup of a group G. H is normal if and only if for every object x in G, xH = Hx.
Notation: HH = H.
x is in HH ==>
x = h1h2 ==> [for some h1 in H and h2 in H]
x = h ==> [where h = h1h2 and therefore h is in H]
x is in H. [1.4]
H = eH ==> H ⊆ HH.
Notation: if aH and bH are left cosets of a normal subgroup H, then product (aH)(bH) = (ab)H.
x is in (Ha)(bH) <==> [H is normal]
x = (h1a)(bh2) <==> [1.4]
x = h1(ab)h2 <==> [associative law]
x is in H(ab)H <==> [1.4]
x is in (ab)HH <==> [H is normal]
x is in abH. [Lemma1]
Notation: if H is a normal subgroup of G, then the collection of all left cosets {aH, bH, cH, dH, eH, ...} form a group.
(b) To show combining left cosets is associative: aH(bHcH) = aH(bc)H = a(bc)HH = (ab)cHH = (ab)HcH = (aHbH)cH, where lemma2 and normalcy of H are used more than once.
(c) eH is the identity: (eH)(aH) = (ea)H = aH, and (He)(Ha) = (eH)(aH) = aH = Ha.
(d) The inverse of aH is a-1H because (aH)(a-1H) = (aa-1)H = eH. Similarly, (a-1H)aH = eH.