China England France Germany Italy Japan Spain USA
Carl F T T T T F T T
Jim T T F F F T F T
Rhonda F T T F T F F T
Sue T F T F F T T T
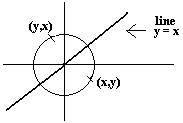An example is the equation of a circle of radius 4. x ~ y if (x,y) satisfies the equation x2 + y2 = 16. If (x,y) satisfies the equation then (y,x) also satisfies the equation. The relation-set is symmetric about the diagonal line with the equation y=x. A diameter is part of that line.
[3.1]
The following are trivial statements about equality:
[3.1r] a=a
[3.1s] if a=b then b=a
[3.1t] if a=b and if b=c then a=c.
Suppose a and b denote different objects, but those objects are so much alike that they appear identical. Strictly speaking a and b are not equal. They do not denote the same object. Instead they denote equivalent objects.
[3.2] Two objects are equivalent if any distinguishing properties are ignored.
At the food store, two oranges are equivalent if the different number of molecules is ignored, if one weighs slightly more than the other, all blemishes are ignored, they are in different positions in the display shelf,.... . A worker asks for any hammer on a table containing several hammers. To him the different hammers are equivalent. Any one of them will allow him to fulfil the task that he has.
[3.3] Two objects are equivalent if either can be replaced by the other. (Allow any object to be replaced by itself).
Recall that the notation x ~ y means that "...x is related to y..."
[3.4] A relation ~ becomes an equivalence relation if ~ has the following three properties for any objects (elements) x,y,z:
[3.4r] (reflexive) x~x
[3.4s] (symmetric) if x~y then y~x
[3.4t] (transitive) if x~y and if y~z then x~z.
In the universe of people, the relation "...is a brother or sister of..." is an equivalence relation.
In the universe U = {1,2,3,4,5,6,7} the following are subsets {1,4}, {3,7}, {2,5,6}. Define the relation ~ by x ~ y if and only if x,y are in the same subset. Then ~ is an equivalence relation.
Using three colors paint the elements of J9 = {0,1,2,3,4,5,6,7,8} to get the set U = {0,1,2, 3,4,5, 6,7,8}. Define a relation ~ on U as follows:
Although U in the previous example is more colorful than J9 it is possible to get the same relation without colors on J9.
(#)
{0,3,6}, {1,4,7}, {2,5,8}
are subsets of J9. Define relation ~ as follows:
For any point x it is possible to create a line through x and parallel to Lo. Therefore x ~ x.
If points x ~ y then the line through them is parallel to Lo. The same line passes through y and x. Therefore, y~x.
If x~y and y~z then all three points x,y,z are on a common line parallel to Lo.
From these remarks, ~ is an equivalence relation. The equivalence classes are all the lines parallel to Lo. They cover the entire plane. Also any two such lines are distinct or coincident.
The relations "is congruent to" and "is similar to" are equivalence relations on geometric figures.
Notice that there is a conflict of notation between elements and sets and points and lines. In traditional geometry, points are assigned capital letters, and lines small letters. In this discussion the notation for elements (small letters) and sets (capital letters) is used.
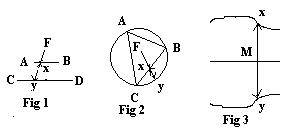
Fig 1 To construct a one-to-one correspondence between two parallel line segments AB and CD of different lengths. Let F be the fixed point of intersection of lines CA and DB (not drawn). A line through F down through a moving point x on AB intersecting CD at y. Then x <--> y is a one-to-one correspondence between the two line segments.
Fig 2 Let ABC be a triangle inscribed in a circle with center at F. Let y be a point moving around the circle and x and let x be the intersection of the radius from F to y and the triangle. Then x <--> y is a one-to-one correspondence between the triangle and the circle.
Fig 3 Two curves are a reflection of each other about a line. A point M moves about the line. Perpendicular to the line at M is line meeting the two curves at x and y. Then x <--> y is a one-to-one correspondence.
[a] A set is countably infinite if and only if it has the same number of elements as the set P of all positive integers.
This definition for infinite sets paralles the definition [3.8] for finite sets. Every finite set has a non-negative number n associated with it, namely the number of elements in the set. It is customary to assign a transfinite number to any countably infinite set, namely the last letter in the Greek alphabet &omega. It is called the cardinal number of any countably infinite set.
The set 2P = {2,4,6,...} of positive even integers is countably infinite because the relation x<->2x is a one-to-one correspondence between P and 2P. A similar fact exists for the set 2J of all even integers (positive, even and zero). Both 2P and 2J have cardinality &omega.
The subset 2P-1 = {1,3,5,7,...} of all odd positive integers is also countably infinite, and together with the subset 2P of all even positive integers form a partition of the set P of all positive integers.
The following facts about infinite sets are given here without being proved.
[b] The set of all rational numbers is countably infinite. (However, click here for further discussion.)
A rational number is a ratio of integers, such as 2/3, -5/2, ... The integers such as 7 are identified as a rational numbers by dividing them by 1: 7/1.
[c] The set R of all real numbers is infinite but not countably infinite.
There cannot exist a one-to-one correspondence between P and R. In an intuitive sense, R is "bigger" than P. Moreover, R is not the "ultimate" infinite set. There exist other sets "bigger" than R!
[d] Every infinite subset of a countably infinite set is countable.
[e] A set is infinite if and only if it has the same number of elements as some proper subset.
[f] A set is infinite if and only if it has a subset that is countably infinite.
The set P of positive integers is a proper countably infinite subset of the set R of real numbers. The set 2P of even positive integers is a proper countably infinite subset of P
and has the same number of elements as P.
If a set U has exactly n elements then the product UxU has n2 elements, which is more than n for n>1. This is different for countably infinite sets. For example, PxP, where P = {1,2,3,...} is the set of all positive integers, has the same number of elements as P itself.
---------
[g]
The product space PxP is countably infinite.
The method to show this is to partition the set N of positive integers into an infinite number of infinite subsets. Start with number 1. Double it to get 2. Double that to get 4. Double that to get 8. Continuing this process of doubling indefinitely to get an infinite subset of powers of 2:
A typical subset starts with an odd positive integer. Other numbers in that same subset are obtained by multiplying that odd integer by enough 2's. Let a be that odd integer. Then the typical set is
If x and y are any numbers in the typical subset then x = (some power of 2)a and y = (some power of 2)a, say x = 2ma and y = 2n. Then the quotient x/y = 2m-n = some power of 2. Allow negative exponents and allow zero as an exponent. This is to say that x and y are in the same subset if and only if their quotient is some power of 2. This, in turn, suggests the following relation on the set N of positive integers:
The relation is reflexive: x ~ x because x/x = 1 = 20.
The relation is symmetric:
x ~ y =>
x/y is a power of 2 =>
y/x is a power of 2 =>
y ~ x.
The relation is transitive:
x ~ y and y ~ z =>
x/y is a power of 2 and y/z is a power of 2 =>
(x/y)(y/z) is a power of 2 =>
x/z is a power of 2 =>
x ~ z.
Therefore the subsets T1=[1], T2= [3], T3=[5], ... are disjoint equivalence classes. The one-to-one correspondence i <-> Ti shows that there are ω subsets (equivalence classes). Therefore, ωxω = ω.
Theorem The set NxN and N have the same number of elements. The ordered pair (i,j) and the number (2i - 1)2j-1 form a one-to-one correspondence between N and NxN.
To prove this start by placing contents of all the subsets T1, T2, T3 ... into a table as rows of black numbers:
1 2 3 4 5 6 ... 1 1 2 4 8 16 32 ... 2 3 6 12 24 48 96 ... 3 5 10 20 40 80 160 ... 4 7 14 28 56 112 224 ... ......................................................................................................... ...
The numbers in red and blue are used to locate places in the table of black numbers. For example, the number in row 3 and column 4 is 40.
Numbers in row 1 and column 1 are very black because they have special properties.
(1) The numbers in row 1 are powers of 2. Comparing each of them with the column numbers above them, a formula appears: 2(column number) - 1 gives very black number below it.
(2) The very black numbers in column 1 are all the positive odd integers. Comparing them with the row numbers to the left shows that the formula 2(row number) -1 gives the very black number in the table to the right.
(3) The product of the very black numbers give numbers inside the table. For example, in row 3 and column 4 the very black numbers are 5 and 8. Their product is 40. If the red and blue numbers are removed what is left is a limited multiplication table of black and very black numbers.
Let i and j be row and column numbers. Then (i,j) locates a (black) number in the table. From statements in (1),(2),(3)
Note: this last statement establishes a one-to-one correspondence between ordered pairs of positive integers and all the integers in the set N:
Given the number 1664 in N, find the row i and column j where the number lies. First divide the number by 2 enough times to get an odd integer. Count the number of divisions.
This process can be used to find the row and column that any number is in N. So every integer appears at least once on the right side of the correspondence. Suppose that the same number appears twice on the right side. The two locations of that number are (i,j) and (x,y). Therefore, (2i-1)2j-1 = (2x-1)2y-1. Divide both sides by 2y-1 to get (2i-1)2j-y = 2x-1. If j is not equal to y then the situation is an odd number times an even number = an odd number, which is impossible. so j = y. This forces 2i-1 = 2x-1. So i = x. Therefore, the number cannot be in two different locations. It appears once and only once among the black numbers.