Go to other chapters or to other books of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Chapter 2 Relations and Products of Sets
Section 1 Relations and Truth Sets of Ordered Pairs
Among all the people on the earth there are relations between them. Expressions like
"is a parent of",
"is a sibling of" (sibling = brother or sister),
"is married to",
"is taller than",
"has more money than"
are relations between two people. Any of these relations produce true statements for some pairs of people, false for others. They can be given in the form of open statements:
x is a parent of y,
x is a sibling of y,
x is married to y,
x is taller than y,
x has more money than y
The idea of relations can be extended to objects. The following is an example.
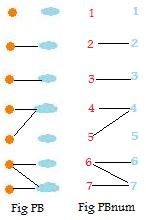
Seven boats are tied up at a dock where there are seven poles. The adjacent figure PB shows how they are tied to the poles. One pole has nothing tied to it. Two boats are not tied to any poles (anchors are used instead). Two boats are so big that they must be tied to two poles. To distinguish poles and boats replace them by numerical labels from P7 = {1,2,3,4,5,6,7} for the poles and labels from P7 = {1,2,3,4,5,6,7} for the boats. (See Fig PBnum). Here P7 and P7 must be considered separate sets because poles and boats are different.
The labels allow the formation of the open statement:
x is tied to y
These ropes relate some poles to some boats physically.
The idea of a relation is important enough to deserve a special symbol, ~ (tilde). It has the literal meaning of "is related to" between elements
pole x ~ boat y
if and only if there is a rope that ties x to y
The open statement has true and false components. The seven TRUE components (represented by the seven ropes) are
(*)
2 ~ 2,
3 ~ 3,
4 ~ 4,
5 ~ 4,
6 ~ 6,
6 ~ 7,
7 ~ 7,
It can be said, that in each of the following pairs, the first element is NOT related to the second element:
1,1,
1, 7,
2, 3,
5, 5,
6, 2,
6, 3,
7, 4,
...................etc
These are some of the 42 pairs of unrelated elements representing the 42 false ordered pairs.
The notation x ~ y means that x is truly related to y. If they are not related, then the expression takes the form of a simple statement: x, y are not related.
The same tilde (~) will also be used between sets containing related elements:
set of poles ~ set of boats
~ is a relation from the set of poles to the set of boats
There is seldom any confusion caused by the dual use of the relation symbol or the words representing it.
The following table of truth values of the relation between elements shows what pole numbers are related to what boat numbers and what are not related. T=true, meaning related, F=false, meaning not related.
(**)
1 2 3 4 5 6 7
1
F F F F F F F
2
F T F F F F F
3
F F T F F F F
4
F F F T F F F
5
F F F T F F F
6
F F F F F T T
7
F F F F F F T
The red integers are the row numbers and the blue integers are the column numbers.
To see if 5 is truly related to 4, in other words to see if 5 ~ 4, draw a horizontal line through 5 and a vertical line through 4, and where the lines intersect is a letter T.
There are two extreme relations.
(1) None of the elements in the first set are related to any elements of the second set. (None of the poles are tied to any of the boats. No ropes are in use.)
(2) Every element in the first set is related to every element in the second set. (All of the poles are tied to all of the boats. 49 ropes are needed.)
Usually these relations are not of interest. For this reason, they are called the trivial relations.
No relation from one set to another can exist if either set is empty.
Consider now two sets P2 = {1,2} and A = {a,b,c} and a table of truth values:
a b c
1 T F F
2 F T T
From this table it is possible to determine which numbers are (truly) related to which letters:
These are related:
(*) 1 ~ a, 2 ~ b, 2 ~ c.
The pairs 1,b, 1,c, 2,a
are unrelated.
A third set B = {X,Y,Z,W} enters into the consideration. The following define a relation from set A to set B:
(**)
a~Z,
a~W,
b~Y,
b~W,
Consider 1,2 as sections of city P2, a,b,c as sections of city A, X,Y,Z,W as sections of city B. The relations are roads connecting sections of a city to sections of another city. The following are roads from P2 to A to B (except for the last one; it is only from P2 to A):
1~a~Z
1~a~W
2~b~Y
2~b~W
1~a
The roads through sections of city A can be combined by paving over the connections and omitting city A to get roads (relation ~) directly linking P2 and B:
(***)
1~Z
1~W
2~Y
2~W
If x ~ y consider interchanging x and y. If y is related to x after the interchange, write y ~ x. A different colored relation symbol ~ is used because this involves a new relation. It is from A to P2 . This new relation is called the inverse relation of ~.
[1.1]
Let ~ be a relation from set U to V. To get the inverse relation ~ of ~ from V to U (notice the order), invert every pair u ~ v to get v ~ u, and retain the truth value.
In the above example,
a ~ 1, b ~ 2, c ~ 2 are true
and the pairs
a,2, b,1 c,1 are unrelated (using the inverse relation).
Click here to get more discussions of inverse relations.
If the sets have only a few elements each, then any relation may be defined by specifying what elements are related to what elements, and/or a table of truth values may be made. But for sets with many or infinite number of elements an open statement in two variables may be used used to define the relation.
For example,
x ~ y if and only if y = x/2
is an open statement that defines a relation from integers to real numbers. (x ~ y is used in place of p(x,y).) It relates 5 to 5/2 but does not relate 7 to 50, because 50 is not equal to 7/2. Incidentally the inverse relation is defined by:
y ~ x if and only if x = 2y.
---------------------------
In each of the above discussions more than one set was involved. But there is no restriction that the sets must be different. A relation on a set is a relation from the set to itself. Such a relation relates elements to elements in the same set. It does not relate anything in the set to anything outside the set, nor anything outside the set to anything in the set.
An inequality < (less than) is a familiar example of a relation on the set of integers J. 4 < 5 is true but 8 < -6 is false, 8, -6 are not related using this inequality relation.
On the set of all logical statements, equivalence is a relation:
p ~ q if and only if p has the same truth value as q
On the set of all triangles in elementary geometry congruence is a relation:
triangle a ~ triangle b a can be moved to coincide with b
The symbol <= , meaning less than or equal to, is considered a single relation. Let this be a relation on the set P4 = {1,2,3,4}:
x ~ y if and only if x is less than or equal to y
The following pairs are all the related numbers in P4:
1~1, 1~2, 1~3, 1~4, 2~2, 2~3, 2~4, 3~3, 3~4, 4~4
The numbers related to 3 are 1,2,3. They form a set [3] = {1,2,3}. Similarly [2] = {1,2}. Also [4] = P4. In general, [a] = set of all elements related to a = set of all x such that x ~ a. This idea is used in a discussion following the next example.
A bag contains a mixed set U of 9 balls, 4 identical red balls, 3 identical green balls, and 2 identical blue balls. The colors allow the creation of a relation on U:
balls are related if and only if they have the same color. (Allow any ball to be related to itself.)
 The bag can be emptied onto a table and the balls randomly come out of the bag one at a time, as shown in the adjacent Fig U.
The bag can be emptied onto a table and the balls randomly come out of the bag one at a time, as shown in the adjacent Fig U.
 Then the balls are collected into subsets of related balls. There are three separate subsets as shown in Fig 3subs. In each subset, every ball is equivalent to every ball, including itself, because they are all identical and have the same color. Since the 3 subsets are disjoint and contain all of the 9 balls, the subsets form a partition of the original set U.
Then the balls are collected into subsets of related balls. There are three separate subsets as shown in Fig 3subs. In each subset, every ball is equivalent to every ball, including itself, because they are all identical and have the same color. Since the 3 subsets are disjoint and contain all of the 9 balls, the subsets form a partition of the original set U.
Painting the balls differently, fewer reds, more blues and greens, but every ball gets painted, will create different relations on U. And different partitions are produced.
Painting the balls as done above produces a a special relation on the set U with three special properties:
[1.2r] (Reflexive) Every element in the set is related to itself.
Every ball in U has the same color as itself.
If a first ball has the same color as the second ball, then the second ball has the same color as the first ball.
[1.2s] (Symmetric) If any element is related to a second element, then that second element is related to the first element.
If a first ball has the same color as a second ball, and the second ball has the same color as a third ball, then the first ball has the same color as the third ball.
[1.2t] (Transitive) if one element is related to a second element, and the second element is related to a third element, then the first element is related to the third element.
[1.3]
If a relation on a set satisfies all three conditions, reflexive, symmetric, transitive, then the relation will produce a partition of the set. The relation is called an equivalence relation and each subset in the partition is called an equivalence class. Click here here to see a discussion of the proof of [1.3].
There is a common notation for equivalence classes. If a is any element, then [a] is the set (equivalence class) of all elements related to a: x is in [a] if and only if x ~ a.
Suppose the colored balls in U are given corresponding colored numbers from P9 = {1,2,3,4,5,6,7,8,9} as they randomly emerge from the bag:
{1,2,3,4,5,6,7,8,9}
Then for each number representing a ball of that color,
[1] = {1,3,5,8},
[2] = {2,6},
[3] = {1,3,5,8},
[4] = {4,7,9},
[5] = {1,3,5,8},
[6] = {2,6},
[7] = {4,7,9},
[8] = {1,3,5,8},
[9] = {4,7,9}
Notice that any two equivalence classes are equal or disjoint: [x] = [y] or [x]/\[y] is empty.
[1.4]
Relations on a set produce partitions (equivalence classes) of that set if and only if the relations are equivalence relations.
Click here for a discussion of this statement.
Section 2 Products of Sets and Truth Sets of Relations
Consider two sets, P2 = {1,2} and Q = {a,b,c,d,e}. No relation has been given between these two sets. However, a table of locations can be made in preparation for the truth values of a relation to be given later:
a b c d e
1 . . . . .
2 . . . . .
Each dot in the table is one of ten locations. Using the notation of plotting points in the coordinate plane of elementary algebra, locate the places with ordered pairs of elements enclosed in parentheses:
(1,a), (1,b), (1,c), (1,d), (1,e),
(2,a), (2,b), (2,c), (2,d), (2,e)
All of these ordered pairs form a set of ten elements. That set is called the cross product of P2 and Q. Notation: P2 x Q.
[2.1]
The cross product or product set of two sets U and V is the set of all ordered pairs (u,v) where u runs through all of U and v runs through all of V.
Notation: U x V
u is called the first coordinate of the ordered pair, and v is called the second coordinate.
[2.2]
Two ordered pairs are equal if and only if their first coordinates are equal and their second coordinates are equal.
(u,v) = (a,b) if and only if u = a and v = b.
For example, the simultaneous equations
x + y = 9
x - y = 5
can be written as:
(x + y,x - y) = (9,5)
An equality between two ordered pairs is equivalent to two equalities.
As a result of [2.2], (u,v) is not the same as (v,u) unless u = v. (Hence the word "ordered" in "ordered pairs.") This also means that the product sets UxV and VxU are different if U and V are different.
If R denotes the set of real numbers (or the real line) then the product set RxR is the coordinate plane used in elementary algebra. Ordered pairs (x,y) are used to locate points in this plane.
It is easy to extend [2.1] and [2.2] to ordered triples (u,v,w) and product sets UxVxW. RxRxR is the 3-dimensional space of solid analytic geometry. Ordered triples (x,y,z) are used to locate points in space.
Suppose a relation ~ is defined from P2 = {1,2} to Q = {a,b,c,d,e} by listing the related elements:
1~a, 1~c, 1~d, 2~b, 2~d, 2~e
These can be converted into ordered pairs:
(1,a), (1,c), (1,d), (2,b), (2,d), (2,e)
Each of these may be concidered as a location in a table. These locations contain a T. So each of these six ordered pairs have been assigned a truth value of T. The remaining ordered pairs of P2 x Q are (1,b), (1,e), (2,a), (2,c) and they are assigned an F.
[2.3]
A relation from set U to V imposes an assignment of truth values to each ordered pair in the product set UxV by the rules:
[a] an ordered pair receives a T if and only if the first coordinate is related to the second coordinate;
[b] All ordered pairs of unrelated elements are given an F.
In symbols,
(u,v) is assigned a T if and only if u is related to v
A relation that relates elements in one set with elements in another set always assigns truth values to every ordered pair in the product set. The subset of all ordered pairs that receive T's is usually the subset of interest.
[2.4]
The subset of all ordered pairs in a product of two sets (they may be equal sets) that are assigned T's from some relation involving elements of the sets is called the truth set (of ordered pairs) of that relation.
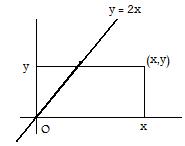
In certain situations it is called the solution set of the relation.
The equation y=2x is actually a relation from real numbers to real numbers, true for those numbers x,y that satisfy the equation, false for those that do not. The truth set is a straight line in the coordinate plane.
The truth set of ordered pairs provides a method to identify equal relations.
[2.5]
Two relations on the same set are equal if and only if they have the same truth set of ordered pairs.
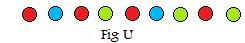 The bag can be emptied onto a table and the balls randomly come out of the bag one at a time, as shown in the adjacent Fig U.
The bag can be emptied onto a table and the balls randomly come out of the bag one at a time, as shown in the adjacent Fig U.
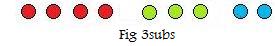 Then the balls are collected into subsets of related balls. There are three separate subsets as shown in Fig 3subs. In each subset, every ball is equivalent to every ball, including itself, because they are all identical and have the same color. Since the 3 subsets are disjoint and contain all of the 9 balls, the subsets form a partition of the original set U.
Then the balls are collected into subsets of related balls. There are three separate subsets as shown in Fig 3subs. In each subset, every ball is equivalent to every ball, including itself, because they are all identical and have the same color. Since the 3 subsets are disjoint and contain all of the 9 balls, the subsets form a partition of the original set U.

