CHAPTER 2

Section 2.1 Paths and Connections

In this section the idea of the edge of a ugraph will be generalized. Let A and B denote the end points of some edge. The nodes A and B are connected by that edge. Now let B and C be the end points of another edge, adjacent to edge AB. The two adjacent edges create a pathway between nodes A and C. Motion can go from A to C (and also from C to A). So A and C are connected. See Fig 2.1a. More adjacent edges may be there after C to create a longer pathway to a distant node, say W. Intuitive "definitions" follow:

A path between two nodes in a ugraph is a chain of adjacent edges joining those two nodes. If a path exists between two nodes then those two nodes are connected. The two nodes are end points of the path. Motion going from one end point to the other is said to traverse the path.

In Fig 2.1b nodes A and W are connected by a path between them. Nodes A and W are end points of the path. Motion going from A to W or from W to A traverses the path.

Of course all edges and paths belong to some ugraph.

It will be convenient to allow every node to be connected to itself. However, no edge is there to do the connection.

It will also be convenient to allow the end points of a path of three or more edges to coincide. In Fig 2.1b nodes A=W. The path then is called a loop. (In some text books it is called a cycle or circuit.) See Fig 2.1c. A loop occurs if there are two different paths between two different nodes.



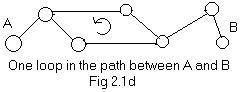
A loop can be part of a path. The path between nodes A and B in Fig 2.1d has one loop. Motion can go from A to B by traversing the loop once.




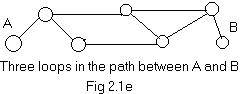
In Fig 2.1e there are several paths and therefore several loops between A and B. Find all the loops and some of the different paths.



In some sense loops present longer paths. A detour by way of a loop presents a longer path because there are more edges to traverse. But loops present a more serious problem for motion. It is possible to traverse a loop many times without leaving it. In fact, it is possible for motion to be "stuck" in a loop by not exiting from it. Characteristic of a loop is the fact that motion must "visit" some node in that loop more than once. There are situations where it is desirable for motion traversing a path not to be able to visit any node more than once. For example, a detective must search thoroughly all the rooms in a house of rooms and corridors. He does not want to waste time searching any room more than once. This is one form of a classic task in graph theory and will be discussed in a later section.

If a path has no loops it is said to be simple.

The paths in Fig 2.1a and Fig 2.1b are simple. The path in Fig 2.1d is not simple. A simple path has two distinct end points. Therefore the path in Fig 2.1c is not simple. As motion traverses a simple path there are no exits from the path at any node along the way. The path shown in Fig 2.1e is not simple because motion must make a decision at the next node after leaving A.

A ugraph "all in one piece" means that all parts of it are connected together. An unbroken path exists between any two parts. This leads to the following definition:

A ugraph is connected if every pair of nodes in it are connected.

The cities, towns and roads in the state of Nevada (USA) form a connected ugraph. The state of Hawaii consists of several islands with cities, towns and roads. The entire system there is a ugraph in several pieces and is not connected. But the system on each island can be represented as a connected subgraph.

Quite naturally a question arises at this point. are two specific nodes in some ugraph connected? The first thought is to look at the drawing of the ugraph. But even there the ugraph may be too large and complicated to be of much help. And the adjacency array does not reveal any connection.

The term "unbroken piece" is given a widely used name:

A component of a ugraph containing a node X is the subgraph of all nodes connected to X. The component will be denoted by [X].

By its definition a component is a connected subgraph. And furthermore it is the largest connected subgraph containing X. For that reason any edge in the ugraph is entirely in that component or the edge is entirely outside that component and entirely in some other component. A connected ugraph has exactly one component.

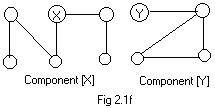Fig 2.11f shows a single ugraph with 10 nodes and 2 components, [X] and [Y]. Component [X] has 6 nodes, component [Y] has 4 nodes. Notice that the components are separated. If there were a path between some node in [X] and some node in [Y] then there would be only one component in the ugraph, and the ugraph would be connected.

In Fig 2.1f X could be placed on any node in the left component. Similarly, Y could be placed on any node in the right component. The names [X] and [Y] of the components remain the same, even though nodes X and Y may have changed.

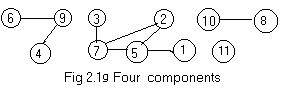Fig 2.1g shows a labeled ugraph with components that can be listed as four clusters of nodes:

A list of components reveals some more information about the basic structure of a ugraph.

Using (#) or Fig 2.1g it is easy to determine if two given nodes in the ugraph are connected. Nodes 1 and 3 are connected, Nodes 4 and 10 are not connected. But from the list of all edges in the ugraph:

 1,5,  2,5,7,  3,7,  4,9,  5,1,2,7,  6,9,  7,2,3,5,  8,10,  9,4,6,  10,8,  11,0//

In a labeled ugraph there is an easily understood notation to indicate a path, called a chain of nodes. It is an extension of the notation for an edge. For example

If a path includes a loop then the chain for that path contains some integer that is repeated. For example in the path containing the loop in the middle component shown in Fig 2.1g, the integer 5 (and also 7) in (##) is repeated. Removing the loop from the path, the path becomes 1-5-7-3 which is simple.

From this section 2.1 goto: additional material / problems / computer programs / facts and theorems


================

Section 2.2 Trees and spanning trees

In this section the idea of being simple will be extended to ugraphs in general. Are there any ugraphs without loops?

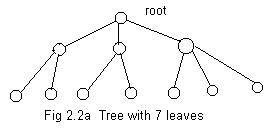
Sometimes a graph is drawn in a shape that can be recognized. Fig 2.2a shows a ugraph in the form of a tree (more like a bush). Actually the tree is drawn upside down. It is traditional to draw it that way, so the root is on top, and the branches (edges) slant downward.

A tree is a connected ugraph with no loops.

The idea of a tree is an extension of the idea of a simple path. A single simple path is equivalent to a straight pole with the base at the top. However, in most situations the "pole" will have downward slanting branches (paths) coming out of it.

Every tree is in one piece and has a one node designated as a root. To any node except the root there is a unique simple path between the root and that node. (In fact for any two distinct nodes in a tree there is a unique simple path joining them.) For motion the root usually serves as an entry point to a tree. Then motion can go down along any branch (edge) to any node below. Somewhere each branch stops at a node where no more branches are growing down. That node is called a leaf. A leaf is a node of degree 1.

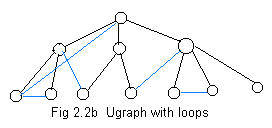In the previous section comments were made against loops in a ugraph Motion along paths without loops (simple paths) were "easier" to traverse. In Fig 2.2b is a ugraph with several loops. If the five blue edges are removed then the tree in Fig 2.2a appears. Although some edges were lost, no nodes were lost. The tree in fig 2.2a is a spanning tree of the connected ugraph in Fig 2.2b.

Of course, it is usually possible to remove other edges from loops to get different spanning trees of the same ugraph. (But the uninteresting discrete graphs provide trivial exceptions.) In additional material for section 2.1 a method using edges to contruct the ugraph indicated what edges that could be omitted to avoid making loops. What is left is given the following definition:

A spanning tree of a ugraph is a connected subgraph without any loops. The spanning tree contains all of the nodes of the ugraph (and most often some of the edges).

A ugraph with a single spanning tree must be connected, because the tree, by definition, is connected, and the tree contains all of the nodes of the ugraph. Because it has no loops a spanning tree is "less complicated" than the entire ugraph, of which the spanning tree is a part (subgraph).

If a ugraph is made up of more than one piece (i.e. has more than one component) then there will be more than one spanning tree involved in order to contain all the nodes.

It seems natural to call any collection of trees a forest. Each tree in a forest is separated from the other trees. Also each tree may have its own unique designated root.

The downward slopes of all edges of a tree suggests direction. If motion starts at a root it goes down (going up is backtracking) along some edges. But it cannot go past a leaf. Being at this "dead end" motion has to back up in order to continue movement.

Besides spanning trees, trees have great importance in graph theory and elsewhere. They provide a popular method for storage and retrival of information (data). One example is the way an operating system, such as Windows or DOS, stores files on a computer disk. They are stored in tree-like structures. In these notes there will be a discussion of data trees later.

From this section 2.2 goto: additional material / problems / computer programs / facts and theorems


===================

Section 2.3 Traversing a labeled ugraph

A fundamental task of graph theory is to discover somehow if two nodes in a ugraph are connected. If they are connected there is no interest yet there is a "best" path between them. Later in these notes there is a discussion about finding the "shortest" path. A common way to find connectivity is to find all the nodes connected to one of the given nodes. If the other node is in the same component then the two nodes are connected by definition of a component. In the additional material to section 2.1 a method was used to find components of a ugraph by reassigning marker labels to components as edges were added in the construction of a ugraph..

In this section another method uses motion. It goes about the ugraph or its application visiting places without getting stuck in loops or dead ends. Also, as a bi-product, the paths of the motion produce a spanning tree (or forests). To provide an intuitive approach the motion is first given a task in a real life physical situation.

A detective must examine extensively all of the rooms in a house (or houses) of rooms and corridors for evidence. The plan of the house(s) is not given to the detective, but fortunately all the rooms are distinctly numbered. The detective knows the numbers of the rooms, so he knows when he has examined all the rooms.

[1] The detective enters any house into the room with the lowest number in that house.

[2] The corridors connecting some rooms may have formed loops. The detective must not get stuck in some loop, traversing it more than once. To avoid this problem he will leave some kind of marker for a room that he has already visited.

[3] In any room where he has a choice of corridors out of the room, the detective chooses to go to an unvisited room with the smallest number.

[4] For any reason if he is in a room and cannot go down any corridor out of it (the room may be a "dead end" with only the entrance into it, or all adjacent rooms have been visited) he then backs up into the room that he previously exited (backtracking). He follows step [3] or [4] or [5].

[5] If the detective is in the room where he entered (see step [1]) and cannot go down any corridor, he backs up out of the house. If there are more houses with rooms to be examined, then he chooses the house with the lowest room number and follows step [1].

[6] His activities stop if all rooms have been examined. There are no more houses to be entered and searched.

In most books on graph theory the procedure is called the depth-first search. (There are other procedures for traversing and searching, such as the breadth-first search.) Extracting the essential parts from the six steps the procedure can be described for a ugraph.

A motion will traversed a labeled ugraph in such a way that every node will be visited once and only once. There is no precondition demanding that all the edges be used.

(1) Enter the component with the unvisited node with the lowest integer label. Start with that node.

(2) Record somehow the integer label of the current node, so that the node will not be visited twice.

(3) At any node look for an unvisited neighboring node with the smallest integer label. If found go along an edge to that room, and repeat step (2). If not, then a standstill exists, and go to step (4).

(4) If no neighboring node exists (dead end in a leaf) or all neighboring nodes have been visited (deadlock), then go backto the previous node visited (backtrack) and go to step (3).
But if motion is at the start node then go to step (5).

(5) If motion is at the start node, and cannot go to any neighboring node (standstill), then motion backs out of the component.
If there are more unvisited components, then go to step (1).

(6) If no unvisited nodes exist, then motion stops.

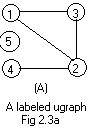Since motion is involved arrows along edges may be convenient to show travel. A ugraph is shown in Fig 2.3a.





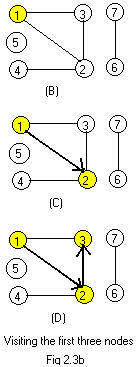Motion starts at node 1. (A)

Indicate that the current node has been visited. Color it yellow. (B)





Motion goes along an edge to node 2 (not to node 3). Color it yellow. (C)





Motion goes along an edge to node 3 (not to node 4). Color it yellow. (D)





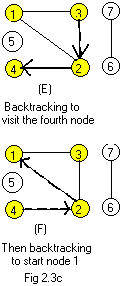Motion is at a standstill at node 3. It cannot go forward because node 1 is yellow. It has been visited. (Deadlock). Therefore motion must go back along the edge 3-2 to node 2.

Motion can go along an edge to node 4. Color it yellow. (E)





(Dead end) Move back along edge 4-2 to node 2. (F)

(Deadlock) Move back along edge 2-1 to node 1. (F)


(Deadlock) Move out of component containing nodes 1,2,3,4.



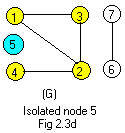
Go to node 5, which has the smallest of the remaining integer labels. Color it blue. (G)
But an isolated node is always a dead end and a component by itself. Back out of this component.




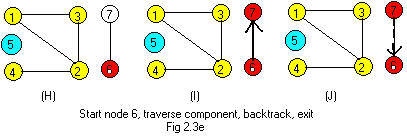The unvisited (colorless) node with the lowest integer label is 6. Color it red. (H)
Move along the edge to the adjacent node 7. Color it red. (I)
That node is a dead end. So go back to node 6. (J)
Exit the component.

All nodes are colored and have been visited. Motion must exit the ugraph.

In traversing the entire ugraph (A) motion used four edges and not edge 1-3. Removing that edge from the ugraph produces a spanning forest.

From this section 2.3 goto: additional material / problems / computer programs / facts and theorems