. No arrow is made along an edge when back tracking.
The back tracking from B may include part or all of the way toward A, but must stop at a node. The directed path from A will always point to the node where the motion is located. See Fig 2.1g.
==================
Section 2.2 Trees and spanning trees
 Sometimes a graph is drawn in a shape that can be recognized. Fig 2.2a shows a ugraph in the form of a tree (more like a bush). Actually the tree is drawn upside down. It is traditional to draw it that way, so the root is on top, and the branches (edges) slant downward.
Sometimes a graph is drawn in a shape that can be recognized. Fig 2.2a shows a ugraph in the form of a tree (more like a bush). Actually the tree is drawn upside down. It is traditional to draw it that way, so the root is on top, and the branches (edges) slant downward.
A tree is a connected ugraph with no loops.
The idea of a tree is an extension of the idea of a simple path. A single simple path is like a straight pole with the base at the top. However, in most situations the "pole" will have downward slanting branches (paths) coming out of it.
Every tree is in one piece and has a single root. To any node except the root there is a unique simple path between the root and that node. For motion the root usually serves as an entry point to a tree. Then motion can go down along any branch (edge) to any node below. Somewhere each branch stops at a node where no more branches are growing down. That node is called a leaf. A leaf is a node of degree 1.
 In the previous section comments were made against loops in a ugraph Motion along paths without loops (simple paths) were "easier" to traverse. In Fig 2.2b is a ugraph with several loops. If the five blue edges are removed then the tree in Fig 2.2a appears. Although some edges were lost, no nodes were lost. The tree in fig 2.2a is a spanning tree of the connected ugraph in Fig 2.2b.
In the previous section comments were made against loops in a ugraph Motion along paths without loops (simple paths) were "easier" to traverse. In Fig 2.2b is a ugraph with several loops. If the five blue edges are removed then the tree in Fig 2.2a appears. Although some edges were lost, no nodes were lost. The tree in fig 2.2a is a spanning tree of the connected ugraph in Fig 2.2b.
Of course, it is usually possible to remove other edges from loops to get different spanning trees of the same ugraph. (But the uninteresting discrete graphs provide exceptions.)
A spanning tree of a ugraph is a connected subgraph without any loops. The spanning tree contains all of the nodes of the ugraph (and most often some of the edges).
A ugraph with a spanning tree must be connected, because the tree, by definition, is connected, and the tree contains all of the nodes of the ugraph. The spanning tree is "less complicated" than the entire ugraph. In fact using the spanning tree there is a path between any pair of nodes and that path is simple and unique.
If a ugraph is made up of more than one piece (i.e. has more than one component) then there will be more than one spanning tree involved in order to contain all the nodes.
It seems natural to call any collection of trees a forest. Each tree in a forest is separated from the other trees. Also each tree has its own unique root.
The downward slopes of all edges of a tree suggests direction. If motion starts at a root it goes down (never up) along some edges. But it cannot go past a leaf. In the next section motion will be used to create a tree made up of arcs (arrows along edges). Go to directed trees for a discussion of trees as special digraphs.
Trees have great importance in graph theory and elsewhere. They serve as a popular method for storage and retrival of information (data), for example the way an operating system, such as Windows or DOS, stores files on a computer disk. They are stored in tree-like structures. In these notes there will be a discussion of data trees later.
===================
Section 2.3 Traversing a connected ugraph
 In the study of graph theory there is a classical problem with an interesting solution. Essentially, the task is for a motion to visit all of the nodes of a ugraph. This process is called traversing the ugraph. The task is made slightly easier if the ugraph is connected (all in one piece). As a by-product the traversing of a connected ugraph will become also be a method for producing a spanning tree of that ugraph.
In the study of graph theory there is a classical problem with an interesting solution. Essentially, the task is for a motion to visit all of the nodes of a ugraph. This process is called traversing the ugraph. The task is made slightly easier if the ugraph is connected (all in one piece). As a by-product the traversing of a connected ugraph will become also be a method for producing a spanning tree of that ugraph.
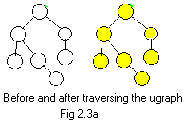
For clarity visited nodes are colored yellow. Unvisited nodes start out as white. See Fig 2.3a.
The task and its solution may be better understood by discussing a real-life situation. The rooms and corridors of a house follow a simple plan shown in Fig 2.3a. A detective must enter the house through one door and examine cmpletely all of the rooms of a house. Corridors make all rooms accessable. The task concludes with the detective's departure from the house through the same door.
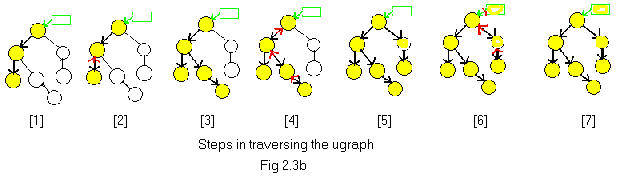
The method of transversing is simple. Go down corridors until he can go no further. (Since the ugraph is a tree, the node will be a leaf.) He enters from the outside with the symbol of a green box. Then he goes down as far as he can go. He passes through three rooms to do this. See Fig 2.3b [1].
His only way out is to backtrack to the previous
room. Fig 2.3b [2].
He sees an unvisited room (white node) down another corridor and goes down it as far as he can. Fig 2.3b [3].
There are still two unvisited rooms (two white nodes). So again he backtracks through several rooms. Fig 2.3b [4].
He sees the two yet unvisited rooms and goes down the corridors into them. Fig 2.3b [5].
He backtracks again all the way to the top room where he entered the house.
There are no more unvisited rooms (all nodes are yellow). So he backs out of the house (into the green box).
All the rooms have been visited. Remove the arrows and see that all the nodes are yellow. See Fig 2.3a.
Several points have been omitted to make the explanation simple. Instead of painting a room yellow to indicate it was visited, the detective could drop a piece of yellow paper onto the floor. Then he could look down all the corridors to adjacent rooms to find a room without a yellow paper.
In the discussion above the ugraph was a tree, so there were no problems caused by loops. But the method of applying yellow can be extended to the general ugraph, which most likely will have loops. It is easier to work with labeled ugraphs. Transversing a labeled ugraph is discussed in additional material.
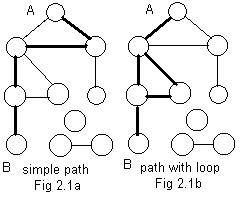 In the previous chapter the idea of a subgraph was introduced. Intuitively, it is part of a bigger graph, some or all of its nodes, and the links for those nodes borrowed from the bigger graph. It is a piece of a bigger graph, without cutting any links in half.
In the previous chapter the idea of a subgraph was introduced. Intuitively, it is part of a bigger graph, some or all of its nodes, and the links for those nodes borrowed from the bigger graph. It is a piece of a bigger graph, without cutting any links in half.
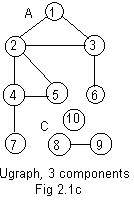 Using only the basic structures of ugraphs it is difficult to give a more precise definition of paths and loops. It is easier using a labeled ugraphs. Using integer labels in Fig 2.1c, the following notation for denoting the path in Fig 2.1a is very obvious in its meaning:
Using only the basic structures of ugraphs it is difficult to give a more precise definition of paths and loops. It is easier using a labeled ugraphs. Using integer labels in Fig 2.1c, the following notation for denoting the path in Fig 2.1a is very obvious in its meaning:
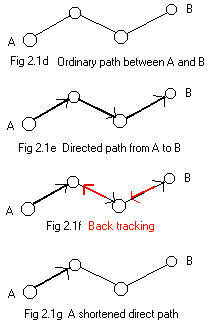 A directed path is a sequence of arcs (arrows) along some (undirected) path from node A to another node B in a ugraph. Each arrow points to the beginning of the next arrow. More precisely, node A is the tail of the first arc, B is the head of the last arc. Inbetween, the node that is the head of any arc is also the tail of the next arc.
See Fig 2.1e.
A directed path is a sequence of arcs (arrows) along some (undirected) path from node A to another node B in a ugraph. Each arrow points to the beginning of the next arrow. More precisely, node A is the tail of the first arc, B is the head of the last arc. Inbetween, the node that is the head of any arc is also the tail of the next arc.
See Fig 2.1e.
 Sometimes a graph is drawn in a shape that can be recognized. Fig 2.2a shows a ugraph in the form of a tree (more like a bush). Actually the tree is drawn upside down. It is traditional to draw it that way, so the root is on top, and the branches (edges) slant downward.
Sometimes a graph is drawn in a shape that can be recognized. Fig 2.2a shows a ugraph in the form of a tree (more like a bush). Actually the tree is drawn upside down. It is traditional to draw it that way, so the root is on top, and the branches (edges) slant downward.
 In the previous section comments were made against loops in a ugraph Motion along paths without loops (simple paths) were "easier" to traverse. In Fig 2.2b is a ugraph with several loops. If the five blue edges are removed then the tree in Fig 2.2a appears. Although some edges were lost, no nodes were lost. The tree in fig 2.2a is a spanning tree of the connected ugraph in Fig 2.2b.
In the previous section comments were made against loops in a ugraph Motion along paths without loops (simple paths) were "easier" to traverse. In Fig 2.2b is a ugraph with several loops. If the five blue edges are removed then the tree in Fig 2.2a appears. Although some edges were lost, no nodes were lost. The tree in fig 2.2a is a spanning tree of the connected ugraph in Fig 2.2b.
 In the study of graph theory there is a classical problem with an interesting solution. Essentially, the task is for a motion to visit all of the nodes of a ugraph. This process is called traversing the ugraph. The task is made slightly easier if the ugraph is connected (all in one piece). As a by-product the traversing of a connected ugraph will become also be a method for producing a spanning tree of that ugraph.
In the study of graph theory there is a classical problem with an interesting solution. Essentially, the task is for a motion to visit all of the nodes of a ugraph. This process is called traversing the ugraph. The task is made slightly easier if the ugraph is connected (all in one piece). As a by-product the traversing of a connected ugraph will become also be a method for producing a spanning tree of that ugraph.
