
Determinants of size 2x2 and 3x3 are used extensively in this chapter to make later formulas more easily understood and remembered. Click here to review a short discussion of them given in Chapter 2.
As the name implies, the vector product produces a third vector from two given vectors. The vectors here are arrays of size 3 (ordered triples). They are of the form (x,y,z), where the coordinates x,y,z are real numbers. The following is the basic but computational definition. (Later in [3.6] is a geometric definition of vector product and it provides direction. That definition may be easier to remember and understand.)
[1.1] (Vector product of two ordered triples) Let p = (x1, y1, z1), and q = (x2, y2, z2) be triples. Then their vector product is the ordered triple:

In inline notation this vector product can be written as
Example. (2,3,4) x (5,6,7) = (--3,6,--3) because
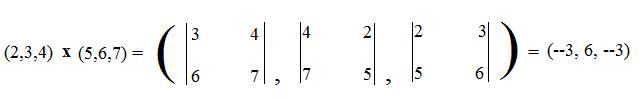
Computing the vector product of two triples is somewhat tedious. Click here to use a computer program for finding vector products directly, without setting up three determinants and finding their values. However, if the vector product is being computed by hand, then there is a simple way to set up the determinants.
Step 1. Repeat the coordinates of (2,3,4) and (5,6,7) twice, the first coordinates above the second coordinates:
2 3 4 2 3 4
5 6 7 5 6 7
Using the second and third columns form the first 2x2 determinant:
2 |3 4| 2 3 4
5 |6 7| 5 6 7
Using the third and fourth columns form the second 2x2 determinant:
2 3 |4 2| 3 4
5 6 |7 5| 6 7
Using the fourth and fifth columns form the third and last 2x2 determinant:
2 3 4 |2 3| 4
5 6 7 |5 6| 7
To get the three determinants:
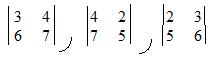
2 3 4 2 3 4
5 6 7 5 6 7
are not used to form any of the three 2x2 determinants.
Some of the properties of vector product are supported by the properties of determinants given in [3.5] in the review of determinants in chapter 2.
[1.2] (Some immediate properties of the vector product)
(a)
The product of the zero vector and any vector is the zero vector: 0 x q = 0.
The product of any vector and the zero vector is the zero vector: p x 0 = 0.
(b) The product of any vector with itself is the zero vector: p x p = 0.
(c) Reversing the order of the product of two vectors negates the vector product: q x p = -- p x q.
(d) If either of two vectors is multiplied by a real number, then the vector product of those vectors is multiplied by that same number:
(λp) x q = λ(p x q);
p x (λq) = λ(p x q).
(e) The vector products of the orthonormal position vectors i = (1,0,0), j = (0,1,0), k = (0,0,1) are as follows:
i x j = k, j x k = i, k x i = j,
j x i = --k, k x j = --i, i x k = --j.
(f) The product of two vectors is the zero vector if and only if either vector is the zero vector or the vectors are parallel:
p x q = 0 if and only if p = 0 or q = 0 or p,q are parallel.
(g) Each of two non-zero vectors is perpendicular to their vector product:
p is perpendicular to p x q and q is perpendicular to p x q.
(h) if the vector product of two vectors is not zero then the two vectors and their vector product form an ordered dextral set.
if p x q is not the zero vector then the ordered set {p, q, p x q} is dextral.
The proofs of parts (a),(b),(c),(d) are based on parts of (a),(b),(c),(d) respectively in [3.5] of the section on determinants in chapter 2.
For the proof of (e), compute the six vector products according to definition [1.1], and for finding the values of the 2x2 determinants, use the simple facts that
[2.1] (Length of a cross product) The norm of a cross product of two position vectors is equal to the product of their norms and the sine of the included angle measured between 0° and 180°
Notation: |p x q| = |p| |q| sin θ
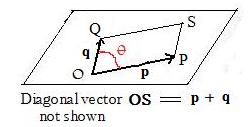 From geometry and trigonometry, the right side of the equation in [2.1] is the formula for the area of a parallelogram OPSQ as shown in the adjacent figure. Therefore,
From geometry and trigonometry, the right side of the equation in [2.1] is the formula for the area of a parallelogram OPSQ as shown in the adjacent figure. Therefore,
[2.2] (Area of a parallelogram) The area of the addition parallelogram for two position vectors is equal to the norm of the vector product of those two vectors.
Notation: |p x q| = area of parallelogram OPSQ, where vertex S is located by the diagonal vector OS = p + q.
Example 1. The area of the parallelogram with three vertices (0,0,0), (2,6,8), (2,5,6) is 6 because the norm of the vector product |(2,6,8) x (2,5,6)| = |(-2,-4,4)| = sqrt(4 + 16 + 16 ) = sqrt(36) = 6. The fourth point of the parallelogram is (2,6,8) + (2,5,6) = (4,11,14) but is not needed in the computation.
Notice that the norm |(2,5,6) x (2,6,8)| = 6, also, because the same parallelogram is involved.
Example 2. Show that (1,1,2), (3,7,10), (3,6,8), (5,12,16) are vertices of a parallelogram and find its area. It is easier to handle if the vertices are moved by subtraction of triples, so that one vertex is at the origin. Subtract the first vertex from all four vertices to get (0,0,0), (2,6,8), (2,5,6), (4,11,14). Since the fourth vertex is the sum of the previous two vertices, the vertices belong to a parallelogram (with one vertex at the origin). Therefore, the given vertices before subtraction are those of a congruent figure and is a parallelogram also. Both parallelograms have areas equal to 6.
Click here to see the equivalent statement in analytic geometry for finding area of a parallelogram with one vertex at the origin.
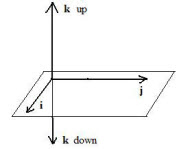
The equation in [2.1] involves the length (norm) of the vector product. It does not determine the direction. Nor does the definition [1.1] of the vector product of two triples determine direction. To discuss direction, start with the simplest situation: the orthonomal (unit) vectors i, j, k, where i x j = k by [1.2e]. Therefore by [1.2g], k is perpendicular to both i and j. The adjacent figure shows that k may point either of two directions, up or down, and still be perpendicular to both i and j. For the convenience of writing vector products in expressions describing physical phenomena, the choice is k = k up. Then --k = k down. Notice that --k = j x i. This suggests that the direction of a vector product depends upon which vector is written first. (See also [1.2c].)
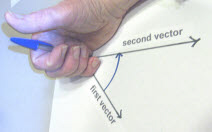 In these pages two methods of determining the direction of a (non-zero) vector product are discussed. Click here for the discussion of an advancing right-hand screw. Discussed now is the right-hand thumb method, as shown in the adjacent figure. At the origin the right hand holds a blue pen which represents the vector product of the two position vectors drawn below. There are two indications of which are the first and second vectors. There is a curved arrow pointing from the first vector to the second vector. The tips of the fingers of the hand point along this curved arrow from the first vector to the second vector.
In these pages two methods of determining the direction of a (non-zero) vector product are discussed. Click here for the discussion of an advancing right-hand screw. Discussed now is the right-hand thumb method, as shown in the adjacent figure. At the origin the right hand holds a blue pen which represents the vector product of the two position vectors drawn below. There are two indications of which are the first and second vectors. There is a curved arrow pointing from the first vector to the second vector. The tips of the fingers of the hand point along this curved arrow from the first vector to the second vector.
The previous paragraph discussed a vector product that did not produce a zero vector, and therefore has a direction. In the following discussion suppose that the vector product p x q is not the zero vector. Then by [2.1] or by [1.2f], neither pnor q can be zero vectors, and the angle θ cannot be 0° nor 180° (meaning p and q cannot be parallel).
If the norm symbols are removed from the left side of equation in [2.1] above, the result is
p x q = |p| |q| sin θ
(angle θ is between 0° and 180°)
This is not a true equation because the left side is a vector, and the right side is a scalar (real number). To make a vector out of the right side and not change the norm of the right side, attach a unit position vector e to the right side to get:
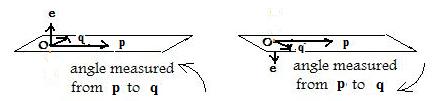
[2.3] (Geometric definition of vector product) The vector product of two non-zero position vectors (in three dimensional space) is equal to the product of their norms and the sine of the included angle and a unit vector that is perpendicular to both given vectors and points in such a direction that the two vectors and the unit vector form a dextral set.
Notation: p x q = |p| |q| sin θ e where e is a unit vector so chosen that p x q is perpendicular to both p and q, and vectors p, q, pxq form a dextral set.
In other words p x q is a vector that is perpendicular to both p and q and points in the direction of the thumb when the fist of the right hand is placed on the origin of the two vectors and the fingers point from p to q.
Because p x q = |p x q| e and the norm is never negative, the vector product p x q and the unit vector e are parallel and point in the same direction. The directions of p x q and e cannot be determined if the vector product is the zero vector.
The vector product gives the area of a parallelogram a direction, and therefore gives that area a vector whose length is the scalar area and direction perpendicular to the parallelogram. This idea can be generalized into assigning vectors to areas inside oriented polygons and simply closed curves.
Consider now three position vectors. There are various ways of combining them using the inner and vector products. Recall that both the inner product and the vector product must be between two vectors, not between a scalar (real number) and a vector which would be meaningless.
A triple inner product, p*q*r is meaningless. (p*q)*r indicates an inner product of a scalar real number (p*q) with a vector r. A similar discussion exists for p*(q*r) which indicates an inner product of a vector and a scalar.
The mixture of products (p x q) * r is meaningful because the vector product is done first. This time the inner product is between two vectors p x q and r. This is so obvious that the parentheses often are not written: p x q * r. (The alternative expression p x (q * r) is meaningless.) This product of three vectors is given a special name, which is derived from its geometrical interpretation. The discussion of this interpretation can be seen by clicking here.
[2.4] (Box product) The box product of three vectors is the inner product of the vector product of the first two vectors and the third vector.
Notation: the box product [pqr] of position vectors p,q,r is [pqr] = p x q * r .
Notice that the box product [pqr] is always a real number, because it is an inner product of two vectors, p x q and r. Since the vector product can be defined by the use of determinants, it can be expected that the box product can be evaluated by the use of a determinant.
[2.5] (Box product and a 3x3 determinant) The value of a box product is equal to a determinant of the coordinates of the points located by the vectors in their order in the box product.
Notation: If position vectors p, q, r locate points
(x1, y1, z1),
(x2, y2, z2),
(x3, y3, z3)
respectively, then the box product [pqr] can be evaluated by inserting the coordinates of the points located by p,q,r in that order into a 3x3 determinant:
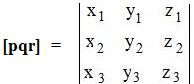
The product p * (q x r) is also meaningful.
[2.6] (Two equal forms of the box product) In the box product the signs of the vector product and the inner product may be interchanged without changing the value of the box product.
Notation: [pqr] = p x q * r = p * q x r
Click here for an algebraic proof of this fact.
A closed rectangular cardboard box is often used for shipping objects packed inside it. It has six faces, and opposite faces are congruent rectangles. Its volume is the product of the length, width and height. If one vertex becomes the origin O and position vectors p,q,r lie on the three edges then the box product p x q * r gives the volume (or it may give the negative volume if the three vectors do not form a right hand set). Hence the name box product.
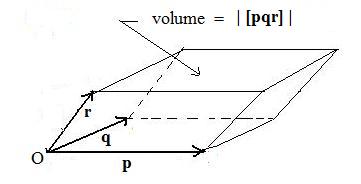 The expression p x q * r is a scalar, and has the geometric interpretation of the volume of a solid called a parallelepiped. A rectangular box is a special parallelepiped with rectangular faces. A parallelepiped has 6 faces that are parallelograms, and opposite faces are congruent parallelograms. A parallelepiped is a sheared box that was once a rectangular box until too much weight was put on the top surface.
The expression p x q * r is a scalar, and has the geometric interpretation of the volume of a solid called a parallelepiped. A rectangular box is a special parallelepiped with rectangular faces. A parallelepiped has 6 faces that are parallelograms, and opposite faces are congruent parallelograms. A parallelepiped is a sheared box that was once a rectangular box until too much weight was put on the top surface.
[2.7] (Volume of a sheared box) The volume of a sheared box with one vertex at the origin is the absolute value of the box product of the three position vectors that make up three sides of the box.
Notation: If p, q, r are position vectors that are also sides of a sheared box, then the volume = |[pqr]| (absolute value).
Click here to see the proof of [2.7].
Another way to combine three vectors is to have two vector product operations. It is equal to a more simple vector expression that does not involve the vector product but does involve the inner product twice and a subtraction.
[2.8] (Triple vector product) The vector product of a first vector with the vector product of a scond vector and a third vector is equal to the inner product of the first and third vectors as a coefficient of the second vector minus the inner product of the first and second vectors as a coefficient of the third vector.
Notation: p x (q x r) = (p*r)q -- (p*q)r.
Click here to see the proof of [2.8]. =============================================================================================================
[4.1] Definition: p x q = (y1z2 − y2z1, z1x2 − z2x1, x1y2 − x2y1) but more easily remembered as

[4.2] Algebraic properties:
(a) q x p = − p x q
(b) p x p = 0
(c) Distributive law: p x (q x r) = p x q + p x r
(d) Scalar associative law: (λp) x q = λ (p x q),
p x (λq) = λ (p x q)
[4.3] Geometric properties
(a) Perpendicularity of vector product: p⋅(p x q) = 0,
q⋅(p x q) = 0
(b) The sine of the angle (between 0° and 180°) between p and q = |p x q/|(|p| |q|)