Return to main page
Additional Material
Vector product of parallel vectors
The vector product of two parallel position vectors is the zero vector.
Let p be any position vector, and let q be a parallel position vector. Then by definition of being parallel, q = λp for some real number λ.
Suppose p = (x,y,z). Then q = λ(x,y,z) = (λx, λy,λz). So the three 2x2 determinants for p x q become:
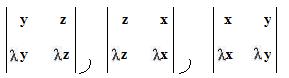 According to the diagonal \ product minus the diagonal / product rule the evaluations of these determinants are:
y λz -- z λy = 0,
z λx -- x λz = 0,
x λy -- y λx = 0
Therefore p x q = (0,0,0) = 0.
According to the diagonal \ product minus the diagonal / product rule the evaluations of these determinants are:
y λz -- z λy = 0,
z λx -- x λz = 0,
x λy -- y λx = 0
Therefore p x q = (0,0,0) = 0.
Each of two non-zero position vectors is perpendicular to their vector product
Let p = (x1, y1, z1), and q = (x2, y2, z2) be triples.
It is advantageous to use the inline notation for vector product:
p x q =
(x1, y1, z1) x (x2, y2, z2) =
(y1z2 -- z1y2,
z1x2 -- x1z2,
x1y2 -- y1x2)
To show that p is perpendicular to p x q it is sufficient to show that the inner product of p and p x q
(x1, y1, z1) * (y1z2 -- z1y2,
z1x2 -- x1z2,
x1y2 -- y1x2)
is equal to the number 0. The inner product results in the left side of the identity
x1(y1z2 -- z1y2) +
y1(z1x2 -- x1z2) +
z1(x1y2 -- y1x2) = 0
The reader can verify this identity with some algebraic computation.
A similar argument proves that q is perpendicular to p x q.
Norm of cross product |p x q| = |p| |q| sin θ
From the algebraic identity for real numbers:
(x1x2 + y1y2 + z1z2)2
+
(y1z2 -- y2z1)2 +
(z1x2 -- z2x1)2 +
(x1y2 -- x2y1)2
=
(x1 + y1 + z1)2
(x2 + y2 + z2)2
the following identity for triples in vector form is produced:
|p*q|2 + |p x q|2
=
|p|2 |q|2
The geometric interpretation of inner product is p*q = |p| |q| cos θ. Therefore, solving for |p x q|2:
|p x q|2
=
|p|2 |q|2 -- |p|2 |q|2 cos2 θ
= |p|2 |q|2 (1 -- cos2 θ)
= |p|2 |q|2 sin2 θ
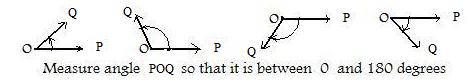
Take square roots of both sides, and remembering that the norm |p x q| cannot be negative, to get:
|p x q| = |p| |q| sin θ
if θ is between 0° and 180°.
Using simple algebra, the two expressions
E1: x1y2(x1y2 -- x2y1) + y1z2(y1z2 -- y2z1) + z1x2(z1x2 -- z2x1)
-- y2z1( y1z2 -- y2z1) -- z2x1(z1x2 -- z2x1) -- x2y1(x1y2 -- x2y1)
E2: (z1x2 -- z2x1)2 + (x1y2 -- x2y1)2 + (y1z2 -- y2z1)2
are equal.
Let p = (x1, y1, z1), and q = (x2, y2, z2).
Then the above equal expressions become respectively the following equal expressions:
E'1: evaluation of the determinant of the ordered set{p, q, p x q}
E'2: |p x q|2
Because p x q is not the zero vector, expression E'2 is a positive real number. Since E'1 = E'2 the value of the deeterminant of {p, q, p x q} is positive and this means that the ordered set {p, q, p x q} is dextral.
Area of a parallelogram
As given in analytic geometry the area of the parallelogram with vertices at
(0,0,0), (x1, y1, z1), (x2, y2,z2)
and (x1 + x2, y1 + y2, z1 + z2)
is equal to
sqrt(
(y1z2 -- y2z1)2 +
(z1x2 -- z2x1)2 +
(x1y2 -- x2y1)2)
The formula for the area involves only triples, not considered as vectors here.
Right hand screw method for direction of vector product
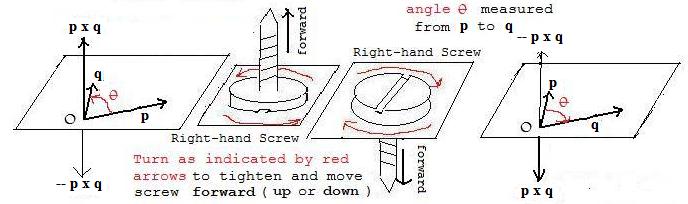
The vector product of two position vectors is perpendicular to both vectors. There are exactly two ways that position vector p x q can be perpendicular to this plane, and those ways are vectors pointing in opposite directions. The angle θ is measured from the first vector p mentioned in the vector product p x q to the second vector q in that same vector product. Always choose the angle that is between 0° and 180°.
Most screws are right-hand screws. This means that if the head of the screw is turned to the right, as indicated by the wavy red arrows in the two center figures, the screw will advance forward into the wood. Now place the screw at the origin O so that the face of the head is in the plane of p,q . At the same time, the direction of θ be the same as the wavy red arrows on the head of the screw. Then p x q will point in the direction of the advancing screw when the head is turned (by a screwdriver). This direction is chosen, and not its opposite, so that vector products can be used in vector equations that more simply model some physical phenomena such as induction coils.
3x3 determinants and their evaluations
The evaluation of the determinant
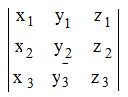 can be done by forming and adding products on diagonals \ \ \ as shown below, and then subtracting products on diagonals / / / as shown below:
can be done by forming and adding products on diagonals \ \ \ as shown below, and then subtracting products on diagonals / / / as shown below:
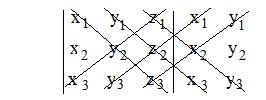
=
x1y2z3 +
y1z2x3 +
z1x2y3 --
z1y2x3 --
x1z2y3 --
y1x2z3
For example, to evaluate the determinant
 draw the diagonals and find the products along each diagonal:
draw the diagonals and find the products along each diagonal:
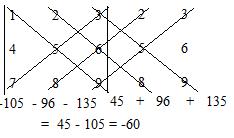
The box product is equal to the value of a 3x3 determinant
Using simple algebra it is possible to show that the following two expressions E1, E3 are equal (algebraic identities):
E1:
(y1z2 -- z1y2) x3 +
(z1x2 -- x1z2) y3 +
(x1y2 -- y1x2) z3
E3:
x1y2z3 +
y1z2x3 +
z1x2y3 --
z1y2x3 --
x1z2y3 --
y1x2z3
If p = (x1, y1, z1),
q = (x2, y2, z2),
r = (x3, y3, z3),
then
expression E1 is equivalent to p x q * r which is the box product [pqr] and
expression E3 is the value of the determinant
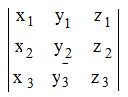 Therefore the box product is equal to the value of this determinant.
Therefore the box product is equal to the value of this determinant.
Switch the vector product and the inner product in a triple of vectors: p x q * r = p * q x r
Using simple algebra it is possible to show that the following three expressions E1, E2, E3 are equal (algebraic identities):
E1:
(y1z2 -- z1y2) x3 +
(z1x2 -- x1z2) y3 +
(x1y2 -- y1x2) z3
E2:
x1 (y2z3 -- z2y3) +
y1 (z2x3 -- x2z3) +
z1 (x2y3 -- y2x3)
E3:
x1y2z3 +
y1z2x3 +
z1x2y3 --
z1y2x3 --
x1z2y3 --
y1x2z3
One way is to multiply out the parentheses in E1 and E2 and show that each of the two resulting expressions are equal to E3 by rearranging the terms. Therefore, expressions E1 and E2 are equal (identities).
If p = (x1, y1, z1),
q = (x2, y2, z2),
r = (x3, y3, z3),
then the expressions E1 and E2 are equivalent respectively to
E'1: p x q * r
E'2: p * q x r
Since expressions E1 and E2 are equal, then these two expressions E'1 and E'2 are equal: p x q * r = p * q x r
A proof from plane geometry of the following theorem
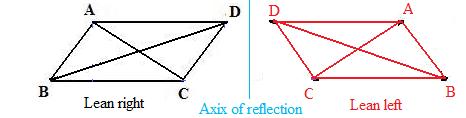
The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of the four sides.
Notation: In the adjacent figures:
AC2 + BD2 = AB2 + BC2 + CD2 + DA2
AC2 + BD2 = AB2 + BC2 + CD2 + DA2
where the red figure is the mirror image of, and therefore congruent to, the black figure. Therefore red segments that correspond to black segments are congruent.segments. Any discussion about the black figure will have a corresponding discussion about the red figure: simply change the color of the words and symbols in the discussion from black to red. Therefore without loss of generality the following discussion will be in black, except for additional lines which are in blue.
Drop a perpendicular from A to line BC meeting that line at M forming right triangles AMC and ABM. Then by the Pythagorean theorem
AC2 = AM2 + MC2,
AB2 = AM2 + BM2
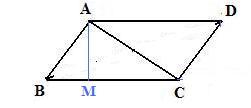 Eliminate AM2 from both equations to get
Eliminate AM2 from both equations to get
AC2 = AB2 + MC2 -- BM2
=
AB2 + (BC -- BM)2 -- BM2
=
AB2 + BC2 -- 2 (BC)(BM) + BM2 -- BM2
(*) AC2 = AB2 + BC2 -- 2 (BC)(BM)
Drop a perpendicular from D to line BC meeting that line at N forming right triangles DNB and DNC. Then by the Pythagorean theorem
BD2 = DN2 + BN2,
DC2 = DN2 + CN2
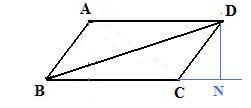 Eliminate DN2 from both equations to get
Eliminate DN2 from both equations to get
BD2 = DC2 + BN2 + CN2
DC2 + (BC +CN)2 -- CN2
=
DC2 + BC2 + 2 (BC)(CN) + CN2 -- CN2
(**)
BD2 = BC2 + CD2 + 2 (BC)(CN)
Therefore, adding equations (*) and (**) above:
AC2 + BD2 = AB2 + BC2 -- 2 (BC)(BM) + BC2 + CD2 + 2 (BC)(CN).
But right triangles ABM and BCN are congruent and therefore CN = BM. Therefore, the terms 2 (BC)(BM) and 2 (BC)(CN) subtract to get zero. Also BC = DA because ABCD is a parallelogram.Therefore,
AC2 + BD2 = AB2 + BC2 + CD2 + DA2
Derivation of perpendicular arrays
Consider two position vectors p and q that locate points P(x1,y1) and Q(x2,y2) respectively. The norms
|p| = sqrt(x12 + y12) and |q| = sqrt(x22 + y22) From elementary algebra
distance between P and Q = sqrt((x1 -- x2)2 + (y1 -- y2)2)
(This distance is also equal to the norm
|QP| = |p -- q| = sqrt((x1 -- x2)2 + (y1 -- y2)2))
 Then p and q are peprendicular if and only if the triangle OPQ is a triangle with a right angle at the origin O (see adjacent figure). By the Pythagorean theorem this is true if and only if PQ2 = OP2 + OQ2. Substitution gives
(x1 -- x2)2 + (y1 -- y2)2 = x12 + y12 + x22 + y22
Squaring out the terms on the left and cancelling like terms on both sides of the resulting equation produces a sum of products equal to zero
x1x2 + y1y2 = 0
A similar argument can be done with perpendicular ordered triples to give
x1x2 + y1y2 + z1z2 = 0
Then p and q are peprendicular if and only if the triangle OPQ is a triangle with a right angle at the origin O (see adjacent figure). By the Pythagorean theorem this is true if and only if PQ2 = OP2 + OQ2. Substitution gives
(x1 -- x2)2 + (y1 -- y2)2 = x12 + y12 + x22 + y22
Squaring out the terms on the left and cancelling like terms on both sides of the resulting equation produces a sum of products equal to zero
x1x2 + y1y2 = 0
A similar argument can be done with perpendicular ordered triples to give
x1x2 + y1y2 + z1z2 = 0
Geometric volume of a sheared box and the box product
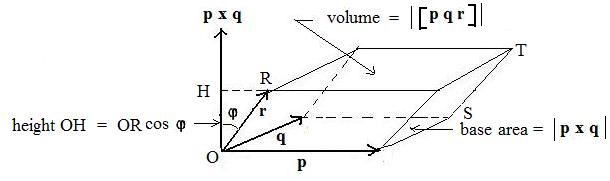 From solid geometry the volume of any cylinder is the area of the (plane) base and the height perpendicular to that base. This is still true even if the base is not a circle but a parallelogram OS and the lines of the side OR of the cylinder are not perpendicular to that base. Let φ denote the angle between a line OH and side OR as shown in the adjacent figure.
By the right triangle rule, OH = OR cos φ. The three position vectors p,q,r form three sides of the sheared box with vertex at the origin O. Then the base has area |p x q|. (See [2.2] in the main page.) The true height of the sheared box is OH which is on the line containing the vector p x q through O. Therefore,
volume OT = area of base OS x height OH = |(|p x q|)(|r| cos φ|= |p x q * r| = |[pqr]|.
From solid geometry the volume of any cylinder is the area of the (plane) base and the height perpendicular to that base. This is still true even if the base is not a circle but a parallelogram OS and the lines of the side OR of the cylinder are not perpendicular to that base. Let φ denote the angle between a line OH and side OR as shown in the adjacent figure.
By the right triangle rule, OH = OR cos φ. The three position vectors p,q,r form three sides of the sheared box with vertex at the origin O. Then the base has area |p x q|. (See [2.2] in the main page.) The true height of the sheared box is OH which is on the line containing the vector p x q through O. Therefore,
volume OT = area of base OS x height OH = |(|p x q|)(|r| cos φ|= |p x q * r| = |[pqr]|.
Evaluation of the triple vector product p x (q x r)
The vector product q x r is perpendicular to the plane of q and r. It is also perpendicular to the expression p x (q x r). Therefore, this triple vector product must lie in the plane of q and r. In other words,
(*) p x (q x r) = λq + σr
for some real numbers λ and σ. It remains to show that λ = p*r and σ = -- p*q.
The rest of the proof is algebraic, but (*) provides some motivation for some steps in this part of the proof.
Using simple algebra it can be shown that the following equations E1, E2, E3 are true
E1:
y1(x2y3 -- y2x3) --
z1(z2x3 -- x2z3) =
x2(y1y3 + z1z3) --
x3(y1y2 + z1z2)
E2:
z1(y2z3 -- z2y3) --
x1(x2y3 -- y2x3) =
y2(x1x3 + z1z3) --
y3(x1x2 + z1z2)
E3:
x1(z2x3 -- x2z3) --
y1(y2z3 -- z2y3) =
z2(x1x3 + y1y3) --
z3(x1x2 + y1y2)
Let
p = (x1, y1, z1),
q = (x2, y2, z2),
r = (x3, y3, z3).
Then
q x r =
(y2z3 -- z2y3, z2x3 -- x2z3, x2y3 -- y2x3)
Hence
p x (q x r) = (left side of E1, left side of E2, left side of E3)
This means that
the x-coordinate of p x (q x r) = left side of E1,
the y-coordinate of p x (q x r) = left side of E2, and
the z-coordinate of p x (q x r) = left side of E3.
Working now with the right sides of equations E1, E2, E3:
right side of E1 = x-coordinate of (p*r)q -- (p*q)r
because
right side of E1 =
x2(y1y3 + z1z3) --
x3(y1y2 + z1z2) =
x2(p*r -- x1 x3) --
x3(p*q -- x1 x2) =
x2p*r -- x3p*q =
x-coordinate of (p*r)q -- (p*q)r,
right side of E2 =
y2(x1x3 + z1z3) --
y3(x1x2 + z1z2) =
y2(p*r -- y1 y3) --
y3(p*q -- y1 y2) =
y2p*r -- y3p*q =
y-coordinate of (p*r)q -- (p*q)r,
right side of E3 =
z2(x1x3 + y1y3) --
z3(x1x2 + y1y2) =
z2(p*r -- z1 z3) --
z3(p*q -- z1 z2) =
z2p*r -- z3p*q =
z-coordinate of (p*r)q -- (p*q)r
Therefore, by way of equations E1, E2, E3,
coordinates of p x (q x r) equal the corresponding coordinates of (p*r)q -- (p*q)r. Therefore,
p x (q x r) = (p*r)q -- (p*q)r.
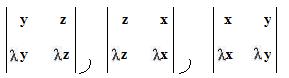
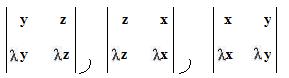
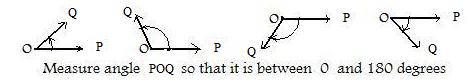

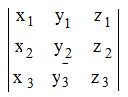



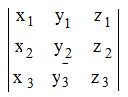

 Eliminate AM2 from both equations to get
Eliminate AM2 from both equations to get Eliminate DN2 from both equations to get
Eliminate DN2 from both equations to get Then p and q are peprendicular if and only if the triangle OPQ is a triangle with a right angle at the origin O (see adjacent figure). By the Pythagorean theorem this is true if and only if PQ2 = OP2 + OQ2. Substitution gives
Then p and q are peprendicular if and only if the triangle OPQ is a triangle with a right angle at the origin O (see adjacent figure). By the Pythagorean theorem this is true if and only if PQ2 = OP2 + OQ2. Substitution gives
 From solid geometry the volume of any cylinder is the area of the (plane) base and the height perpendicular to that base. This is still true even if the base is not a circle but a parallelogram OS and the lines of the side OR of the cylinder are not perpendicular to that base. Let φ denote the angle between a line OH and side OR as shown in the adjacent figure.
By the right triangle rule, OH = OR cos φ. The three position vectors p,q,r form three sides of the sheared box with vertex at the origin O. Then the base has area |p x q|. (See [2.2] in the main page.) The true height of the sheared box is OH which is on the line containing the vector p x q through O. Therefore,
From solid geometry the volume of any cylinder is the area of the (plane) base and the height perpendicular to that base. This is still true even if the base is not a circle but a parallelogram OS and the lines of the side OR of the cylinder are not perpendicular to that base. Let φ denote the angle between a line OH and side OR as shown in the adjacent figure.
By the right triangle rule, OH = OR cos φ. The three position vectors p,q,r form three sides of the sheared box with vertex at the origin O. Then the base has area |p x q|. (See [2.2] in the main page.) The true height of the sheared box is OH which is on the line containing the vector p x q through O. Therefore,