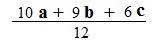
[1.1] (Linear combinations) A linear combination (abbreviation lincomb) of a finite number of vectors is obtained by multiplying each vector by a scalar (real number) and adding up all such products. Those real numbers are called coefficients of the linear combination.
Notation: if a,b,c,d,... are vectors, then a linear combination of them is
In the linear combination above αa, βb, γc, δd ... are terms and α, β, γ, δ ... are coefficients.
Often the abbreviation lincomb will be used to mean linear combination.
For example,
It is quite possible to form a lincomb in which all of the scalar coefficients are (numerically) equal to zero. An example is
If some or all of the coefficients are rational numbers (quotients of integers) it is often convenient to respresent the lincomb as having integer coefficients, and that lincomb is divided by an integer. For example, (5/6)a + (3/4)b + (1/2)c is equivalent to
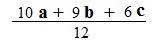
Because it is a sum of vector terms, any lincomb is a vector. A lincomb of position vectors is a position vector and therefore locates a point. For example,
if a, b, c locate points (2,3), (--1,--4), (5,--3) respectively, then 5a + 4b -- 2c locates the point (-4,5) because
5a + 4b -- 2c =
5(2,3) + 4(--1,--4) -- 2(5,--3) =
(10,15) + (--4,--16) + (--10,6) =
(10 -- 4 -- 10, 15 -- 16 + 6) =
(--4,5)
Because it is equal to the zero vector, any trivial lincomb always locates the origin O.
There are two aspects of any lincomb in these discussions: (1) the form of the lincomb itself with its vectors and coefficients, and (2) the point located by the lincomb. Some discussions are more easily understood using located points.
In these discussions, the process of finding the coordinates of the point located by a lincomb is called an evaluation of the lincomb. Obviously, evaluation is only possible if all points located by the position vectors are given as arrays with known coordinates, and all coefficients are known.
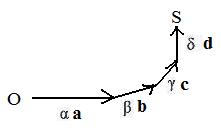
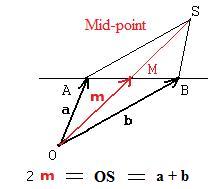
There is a purely geometric interpretation of a lincomb. Let αa + βb + γc + δd be an example. Let S denote the point located by this lincomb. The vector addition of the terms αa, βb, γc, δd can be done by the triangle method. In the adjacent figure the linear combination has formed a directed path from origin O to S. (Paths are studied in more detail in the volume on Graphs.)
A specific lincomb of position vectors may locate a point that has geometric and/or physical relationship to those points located by the position vectors.
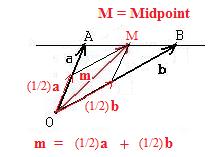[1.2a] (Mid point formula) One-half the position vector locating one endpoint plus one-half the position vector locating the other endpoint produces a lincomb that locates the mid-point of the line segment joining those two endpoints.
Notation: The lincomb (1/2)a + (1/2)b locates a point that is the mid point of segment AB.
Let A and B be the points located by position vectors a and b, Let M be the name of the point midway between A and B. The point M is half the distance from A to B. So vector AM = (1/2)AB. This can be written
m -- a = (1/2)(b -- a)
By simple algebra,
m = (1/2)a + (1/2)b.
Therefore, (1/2)a + (1/2)b locates the mid point of segment AB.
Example, the mid point between (3,6) and (1,4) is (1/2)(3,6) + (1/2)(1,4) = ( (3/2)+(1/2) , (6/2)+(4/2) ) = (2,5).
It is possible to modify the derivation of the mid point formula to use an inline notation which avoids handling many fractions. Starting with
AM = (1/2)AB
multiply both sides by 2 to clear fractions and get
2AM = AB
This means that 2(m -- a) = b -- a. By simple algebra
(#)
2m = a + b
from which follows m = (1/2)a + (1/2)b
The adjacent figure shows the addition parallelogram for a + b = OS. But OS = 2m. From (*), M is the mid point of segment OS. Therefore M is the mid point of both diagonals. This supports the statement from geometry that the diagonals of a parallelogram bisect each other.
Recall that the arithmetic average of a collection of quantities is the sum of all the quantities divided by the number of quantities. This is also true for two position vectors:
(*)
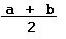is the average of position vectors a and b. The following statement is equivalent to [1.2a]:
[1.2b] (Mid point formula) The average of two position vectors locates the mid point of the segment whose end points are located by the given position vectors.
Notation: The arithmetic average shown in expression (*) above locaates the mid point of segment AB.
Example, the mid point between (3,6) and (1,4) is
The single mid point separates a segment into two congruent pieces. The two points of trisection separate a segment into three congruent pieces.
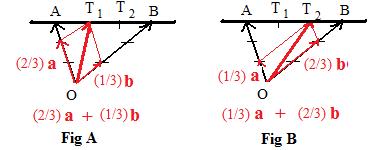[1.3] (Points of trisection) The sum of two thirds of the position vector locating one endpoint and one third of the position vector locating the other endpoint of a segment produces a lincomb that locates the point of trisection nearest the end point located by the position vector with the largest coefficient (multiplying fraction).
Notation: (2/3)a + (1/3)b locates the point of trisection of segment AB nearest A. (Fig A)
Notation: (1/3)a + (2/3)b locates the point of trisection of segment AB nearest B. (Fig B)
2/3 is larger than 1/3. The position vector in the term that has 2/3 as coefficient locates the endpoint nearest the point of trisection. The larger coefficient gives more "weight" to the position vector.
The lincombs exprssed in the Notations for [1.3] can be stated as fractions:
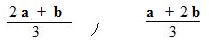
Click here to see derivations of these lincombs and fractional formulas for trisection.
[1.4] (Arbitrary point on a line) A lincomb of two distinct vectors locates a point on the line through the points located by the given vectors if and only if the sum of the coefficients of the lincomb is equal to 1.
Notation: αa + βb locates a point on line AB if and only if α + β = 1.
Example:
Given points A(1,2) and B(4,3). Question: is the point (7/2, 17/6) on the line AB?
Suppose the lincomb α(1,2) + β(4,3) locates the point (7/2, 17/6). To find the values of α and β. Then
(7/2, 17/6) = α(1,2) + β(4,3)
= (1α, 2α) + (4β, 3β)
= (α + 4β, 2α + 3β)
This results in two equations in two unknowns, α and β
α + 4β = 7/2
2α + 3β = 17/6
Solving for the unknowns produces:
α = 1/6, β = 5/6.
Obviously the sum α + β = 1. By [1.4] the lincomb α(1,2) + β(4,3) locates a point on line AB. Therefore, (7/2, 17/6) is a point on line AB.
The reader can show that for the point (--2,1) the coefficients of the lincomb add up to 1, so (--2,1) is also a point on the line AB. However, for the origin (0,0) the coefficients both must be zero, and therefore their sum is zero, not 1. So the origin is not on the line AB.
Click here to see a proof of [1.4].
It is sometimes necessary to handle a lincomb in which the sum of the coefficients is not 1. However, the sum of those coefficients must not be zero. According to [1.4] the lincomb 3a + 2b does not locate any point on line AB because the sum of coefficients = 3 + 2 = 5 which is not 1. But the lincomb (3/5)a + (2/5)b does locate a point on line AB. Similarly, 7a -- 5b does not locate a point on line AB, but (7/2)a -- (5/2)b does. (Moreover, it lies on line AB but outside the segment AB. More exactly, the point A lies between point B and the point located by the lincomb.)
[1.5] (Normalizing coefficients) To normalize the coefficients of a lincomb, where the sum of all coefficients is not zero, means to divide each coefficient by the sum of all coefficients.
Notation: To normalize the coefficients of αa + βb, divide α and β by their sum to get
Here are some facts about normalizing.
(a) Obviously the sum of these new coefficients (fractions) is 1.
(b) Usually the process of normalizing changes the lincomb to a lincomb with different coefficients. However, the new coefficients are proportional to the old coefficients.
(c) It is impossible to normalize the coefficients of a lincomb if the sum of all the coefficients equals zero. (Geometrically, the lincomb is a position vector parallel to line AB)
These statements about normalizing will be referred to as [1.5a], [1.5b], [1.5c].
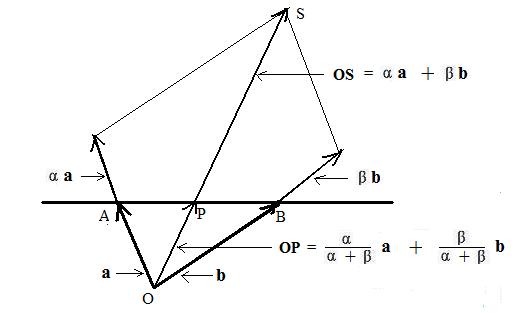Geometric interpretation of normalizing.
Suppose the sum of the coefficients in the lincomb
αa + βb is not 0 nor 1. Then by [1.4] the lincomb locates a point not on line AB. Call the point S. Normalizing the coefficients produces a new lincomb (**) in which the sum of the coefficients is equal to 1. Suppose the new lincomb locates a point P. That point P is on the line AB, again by [1.4]. That point P is also on line OS because OP = (1/(α + β)) OS. Therefore, the division of αa + βb by the sum α + β "adjusts" the length (and possibly the direction to the opposite direction) of the vector OS so that the new vector OP locates a point on the line AB.
Notice that if α + β = 0 then OS = β(b - a) = βAB and then OS is parallel to AB. Then there is no point P of intersection of lines OS and AB. (It could happen that line OS coincides with line AB. Still, no unique point P.)
Let p equal to the lincomb in (**). Then multiply both sides of this equality by the sum α + β to lear fractions and obtain the equation:
[1.6] Two equivalent vector equations for a point on a line) Let A and B be distinct points on a line. The following equations are equivalent conditions that a point P lie on line AB:
Notice that the coefficient of the position vector p is the sum of the coefficients of the lincomb on the other side of the equation. If U and V are distinct points then the existence of the equation (μ + τ)w = μu + τv with real numbers μ and τ guarantees that the point W is on the line through U and V. Again the sum of the real numbers on the left side of the equation equals the sum of the coefficients on the right side. If 7w = 4u + 5v then point W is not on line UV because 7 is not equal to 4 + 5.
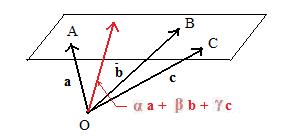
[1.7] (Arbitrary point in a plane) Let three position vectors locate three points that are not collinear. A lincomb of those three vectors locates a point on the plane through the three points if and only if the sum of the coefficients of the lincomb is equal to 1.
Notation: αa + βb + γc locates a point in plane ABC if and only if α + β + γ = 1.
Example:
If A(4,2,6), B(3,0,--6), C(6,12,-6) then the lincomb 3a + 2b + c locates the point (24,18,0). However this point is not in the plane ABC because the coefficients add up to 6, and not 1. The coefficients can be normalized by dividing each coefficient by 6 to get a new lincomb (1/2)a + (1/3)b + (1/6)c which locates the point (3,3,0). This point is in the plane of ABC because the coefficients of the lincomb add up to 1.
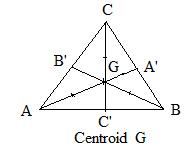
[1.8] (Centroid of a triangle) The three medians which join each vertex to the mid point of the opposite side intersect in a common point. That point is located 2/3 the way from any vertex to the mid point of the opposite side. Also that point is located by a position vector which is the arithmetic average of the position vectors locating the three vertices of the triangle. (The point is called the centroid of the triangle.)
Notation: If A,B,C are the vertices of a triangle, and A', B', C' are mid points of the sides opposite these vertices, then all the following fractions locate the same point (centroid):
(***)
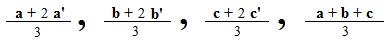
First show that the four numerators are equal. Since A', B', C' are mid points,
Each of these equations has a geometric interpretation. The first says that G is a point of trisection of segment AA' nearest A', the second says that G is a point of trisection of segment BB' nearest B', the third says that G is a point of trisection of segment CC' nearest C'. By [1.7] the fourth says that the lincomb
If a thin disk has the shape of a triangle, then the center of gravity is the point G where the medians intersect. The disk should balance on the tip of a vertical pin. But if the vertices are located at A(4,2,6), B(3,0,--6), C(6,12,-6) and very tiny weights of 1/2, 1/3, 1/6 are placed on the vertices respectively, then the centroid will shift to (3,3,0). See example following [1.7].
If A,B,C are points and weights of α,β,γ, (pounds, kilograms...), whose combined weights might not add up to 1, are placed at those points respectively, then the centroid of this system is located by the the position vector:
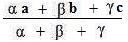
There are similar statements about the "spacial medians" of a tetrahedron, and about 4 weighted points in space. Click here to see the discussions.
[1.9] (Two equivalent vector equations for a point in a plane) Let A,B,C be three non-collinear points in a plane. The following equations are equivalent conditions that a point P be in plane ABC:
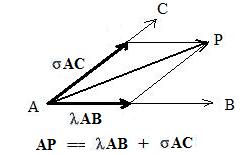
Construct lines through A and through the other two points, B,C. Also, draw vectors AB and AC along the lines. They cannot be parallel nor zero because, by hypothesis, A,B,C do not lie on a common line. It is possible to draw a parallelogram with vertices at A and P and a vertex on each line if and only if P lies in the plane ABC. This parallelogram creates new vectors λAB and σAC along these lines so that the parallelogram is the addition parallelogram for AP = λAB + σAC.
The vectors AP, AB, AC may be replaced by the differences of position vectors to produce the equation
Solve for p in [1.9] to prove the following:
[1.10] (Vector fraction for a plane) For any non-collinear points A,B,C and for any real numbers α,β,γ whose sum is not zero, the fraction
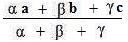
Two or more lincombs are equal if and only if they locate the same point. But there are other ways of comparing lincombs. The sum of all the coefficients in a lincomb may have significance. Two or more linear combinations are in scalar balance if and only if the sums of coefficients of every linear combination are equal.
Notation: linear combinations αa + βb + γc + δd and λu + σv + ωw are in scalar balance
For example, the lincombs 4a + 3b -- 5c + d and 6u + v -- 4w are in scalar balance because 4 + 3 -- 5 + 1 = 6 + 1 -- 4.
Scalar balance is useful only between equal lincombs. (α + β + γ)p = αa + βb + γc is an example. Another example is c + 2c' = a + b + c obtained from (***) above. The proof of some geometric facts by position vectors is often directed toward deriving equal lincombs in scalar balance.
For example, The lincombs
However, if c is the zero vector, then
Lincombs of the same collection of fixed vectors can be added and subtracted to produce new lincombs of the same fixed vectors. If
The idea of a point located by a single lincomb has been discussed. Two lincombs locate two points (the points may coincide or be distinct). A hundred lincombs may locate a hundred points (or less if some points coincide). There are many, many lincombs that can be formed from a collection of fixed vectors, and taken together they locate a set of many points.
[2.1] (Generating points) The set of points located by all lincombs of a collection of fixed vectors is said to be generated by the (collection of) fixed vectors. The collection of fixed vectors is said to generate that set of points. The range of a collection of fixed vectors is the set of points generated by the collection. Also, the collection of fixed vectors is said to span the position vectors that locate the points.
To produce all possible lincombs from a collection of fixed vectors, there must be no restriction on the coefficients. To emphasize this fact, the fixed vectors are said to generate the set of points without restriction on the coefficients of the lincombs.
Example: Often the vectors in the collections {(1,0), (0,1)} and {(1,0,0), (0,1,0), (0,0,1)} will be used as fixed vectors. The linear combinations have the forms x(1,0) + y(0,1) and x(1,0,0) + y(0,1,0) + z(0,0,1) respectively and locate points (x,y) and (x,y,z) respectively. There can be no restrictions on x,y or x,y,z in order to generate a full plane or all of space. Recall that the four linear spaces discussed in these sections are point, line, plane and space. Each of them contains the origin O. The following four statements relate these linear spaces to the number of position vectors that generate them.
[2.1a] (Generating a point) The zero vector generates a single point, the origin O.
[2.1b] (Generating a line) A single non-zero fixed vector generates the line along which the vector lies. A non-zero position vector spans all position vectors along (parallel to) the line through the origin.
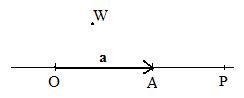Let a be a fixed position vector. Then the vector locates the point A and then there is a line through origin O and A. Intuitively speaking, let α be a variable "running through" all the set of real numbers (takes on all real numbers as values). Then the lincomb αa runs through points on the line OA. Let P be any point on that line OA. If P=O then the trivial lincomb 0a locates P. If P and O are distinct, then let α = OP/OA (ratio of lengths) if O is not between P and A, and let α = --OP/OA if O is between P and A. Then P is located by αa.
If W is any point off of line OA, then there is no value for α so that the lincomb αa locates W. All by itself a generates a line that does not contain W.
[2.1c] (generating a plane) Two fixed non-zero vectors that are not parallel generate the plane containing both vectors.
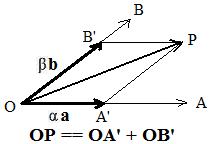In the adjacent figure vectors a and b are represented as vectors OA and OB. Clearly lines OA and OB are not parallel, and intersect at O. Let P be any point in the plane determined by points O,A,B. The points O and P determine a unique parallelogram with sides on the lines. Let A' and B' be points on the lines. Then vectors OA' and OB' are parallel to vectors OA = a and OB = b respectively. Therefore, for some scalars α and β, OA' = αOA and OB' = βOB. This means that OP = OA' + OB' = αa + βb. Therefore, OP = some lincomb of vectors a and b.
If P falls on line OA then since vector a generates line OA, α = OP/OA and β = 0;.Similarly, if P falls on line OB, α=0 and β = OP/OB.
There is an algebraic parallel to the discussion, using ordered pairs (or ordered triples). A specific example is needed. Suppose a = (4,0) and b = (3,6) or equivalently given points A(4,0) and B(3,6). To find coefficients α and β so that the lincomb αa + βb locates the point P(4,4):
In the figure, A' (2,0) because A' is located by αa = (1/2)(4,0) =(2,0). Also B'(2,4) because B' is located by βb = (2/3)(3,6) = (2,4).
It is not necessary but is easily verified that the points O(0,0), A'(2,0), P(4,4), B'(2,4) are vertices of a parallelogram: vectors OA'=(2,0) and B'P = p -- b' = (2,0) are equivalent. In this algebraic discussion, the geometric construction of the parallelogram as done in the figure is replaced by the solving of the simultaneous equations 4α + 3β = 4, 6β = 4.
[2.1d] (generating 3-dimensional space) Three fixed non-zero vectors that do not lie in one plane generate space.
Click here for the discussion of this statement.
In the above four statements it can be said that sets of points generated by not more than three fixed vectors form a single point, a line, a plane or all of space. It is quite possible to develop a similar algebraic discussion of four non-zero fixed vectors generating hyperspace of dimension 4. using arrays of length 4. Or using n fixed arrays of length n to generate hyperspace of dimension n. Not so easy are the corresponding geometric discussions with diagrams. Such discussions are beyond the scope of the material here about fixed vectors.
Let a, b, c be fixed vectors that locate points (1,2,1), (2,--1,1), (8,1,5) respectively. Since
This idea leads to a definition. A vector is dependent upon the other vectors in a collection of fixed vectors if and only if that vector is equal to some lincomb of those other vectors.
Example: in the above discussion, c is dependent upon a and b because c = 2a + 3b.
Because of its dependence, the vector is removable from the collection. After the removal the resulting smaller collection can do everything that the larger collection can do. Intuitively speaking, some vector can be removed from any reducible collection, and nothing is lost by its absence. The reduced collection can function just as well without the missing fixed vector as the original collection with that removable vector.
It may happen that a collection of fixed vectors may be reduced several times. But eventually, a collection is obtained that is not reducible. All the non-essential fixed vectors have been removed. This idea will be discussed later.
[2.2] (Linear dependence (1)) A collection of fixed vectors is linearly dependent if and only if it has at least one dependent vector.
A collection containing the zero vector is always linearly dependent, because the zero vector is dependent upon the remaining vectors. It is equal to the lincomb of those other vectors in which all coefficients are zero real numbers, in other words the trivial lincomb of those other vectors.
Even if it has no zero vectors, a collection may be linearly dependent. It may have non-trivial dependent vectors. In the above example, the collection {a,b,c} is a linearly dependent collection without any zero vectors. The fixed vector c is dependent upon a and b.
The following theorem provides another way of detecting linearly dependent collections of fixed vectors.
[2.3] (Linear dependence (2)) A collection of fixed vectors is linearly dependent if and only if there is a non-trivial lincomb equal to the zero vector.
Let a,b,c,d be fixed vectors. If they are linearly dependent then one vector, say d, is dependent upon the other vectors. Then
Conversely, if there is a non-trivial lincomb of a,b,c,d equal to the zero vector,
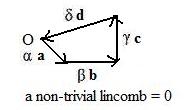Recall that a geometric interpretation of a lincomb is a directed path from the origin to a point located by the lincomb. A geometric interpretation of a non-trivial lincomb equal to the zero vector is a directed path from the origin back to the origin forming a loop. But the trivial lincomb also locates the origin. So there are at least two different lincombs locating the origin. The following is another characteristic property of linear dependence, two paths to the same point.
[2.4] (Linear dependence (3)) A collection of non-zero fixed vectors is linearly dependent if and only if every generated point can be located by two (or more) different lincombs of those same vectors.
In every lincomb the dependent vector can be replaced by its lincomb of the remaining vectors, to create another equal lincomb without the dependent vector. Thus there are two different lincombs locating the same point.
Conversely, if two different lincombs of fixed vectors locate the same point, then the lincombs can be subtracted to create a non-trivial lincomb equal to the zero vector. By [2.3] this makes the collection linearly dependent.
Statements [2.5] and [2.6] below involve a special kind of linear dependence. If three points are picked at random, it is very unlikely that all three lie on a common line. If point C is on the line through points A and B then (α + β)c = αa + βb for some scalars α and β (see discussion just after [2.2] above.) Let γ = --(α + β). This suggests the following:
[2.5] (Collinear points) Three points are collinear if and only if some nontrivial lincomb of their position vectors is equal to the zero vector.
Notation: Three points A,B,C lie on a common line if and only if for some scalars α, β, γ, not all zero, the following vector equation and scalar equation are satisfied:
There is a similar statement about four points in a common plane.
[2.6] (Coplanar points) Four points are coplanar if and only if some nontrivial lincomb of their position vectors is equal to the zero vector.
Notation: Four points A,B,C,D lie in a common plane if and only if for some scalars α, β, γ, δ, not all zero, the following vector equation and scalar equation are satisfied:
The following is like [2.6] except that the coefficients are unrestricted.
[2.7] (Space has dimension 3) For any four points in space their position vectors are linearly dependent.
Notation: For any four points A,B,C,D there exist scalars α, β, γ, δ, not all zero, such that the following vector equation is satisfied:
The proof is more easily done using matrices.
A collection of fixed vectors is linearly independent if and only if the collection is not linearly dependent.
Suppose a locates the point (5,6), and b locates the point (3,4). An attempt here is made to show that b depends upon a. This assumption will lead to a contradiction (Expect an indirect argument because linear independence was defined in a negative definition).
For some number λ, b = λa. Two equations arise from (5,6) = λ(3,4):
There are more convenient ways to show linear independence than the definition just given. A rephrasing of the logically equivalent statements in [2.3] provides a better way.
[2.8] (Linear independence (2)) A collection of fixed vectors is linearly independent if and only if only the trivial lincomb is equal to the zero vector.
Notation: Collection {a,b,c,d,...} is linearly independent if and only if
αa + βb + γc + δd + ... = 0 implies α = β = γ = δ = ... = 0
For example, the position vectors that locate points (1,0) and (0,1) are linearly independent because
Another example. As before, suppose a locates the point (5,6), and b locates the point (3,4). To show that the implication
The following is a useful property of linearly independent fixed vectors. Its geometric interpretation is that there is only one lincomb that creates a directed path to any given point generated by the vectors.
[2.9] (Unique coefficients) If a collection of fixed vectors is linearly independent then the only way that two lincombs can be equal is that corresponding coefficients are equal.
Notation: if {a,b,c,d,...} is a linearly independent collection of fixed vectors then
The uniqueness of coefficients gives importance to the following definition.
[2.10] (Basis) A basis for a set of points is any linearly independent collection of fixed position vectors that generate that set of points.
A basis generates a set of points and the vectors in the basis are linearly independent.
If vectors a = (1,0) and b = (0,1) in the plane of ordered pairs of real numbers, then the collection {a, b} is a basis for all points in that plane.
The collection generates every point in the plane. To show this, let (x,y) be any point in the plane. Then it is easily verified that (x,y) = x(1,0) + y(0,1) = xa + yb, which is a lincomb of vectors locating (x,y).
That a and b are linearly independent was shown in the discussion just after [2.8].
[2.11] (Number of vectors in a basis) The number of vectors in any two bases for the same set of points is the same.
This fact is assumed to be true. It can be proven in discussions of non-singular square matrices.
[2.12] (Dimension) The dimension of a set of points is the number of vectors in any basis for that set.
The statements [2.1a], [2.1b], [2.1c] show bases, and therefore the dimensions 1,2,3 for a line, plane and space respectively. The origin (or any point) has dimension 0. These four sets are called linear spaces. There are linear spaces of higher dimensions, and in fact, of infinite dimensions. The term vector spaces is more often used in books about vectors. In these discussions that term is used to emphasize the position vectors, rather than the points that they locate.
[2.13] If the number of fixed position vectors in a collection is greater than the dimension then the collection is linear dependent.
The statement [2.7] is an example.