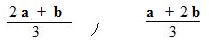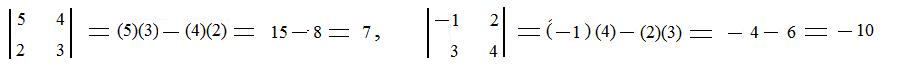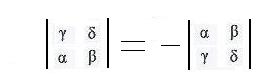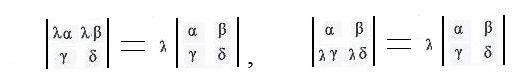Return to main page
Additional Material
Lincomb locates a point on a line
Let αa + βb be a lincomb of distinct vectors a,b and α + β = 1. Let p a + βb Then α = 1 -- β. Therefore, p = αa + βb = a + βAB Subtract a from both sides to get AP = βAB. This forces point P to be somewhere on line AB.
Reversing the steps shows that if P is on the line AB then for some numbers α and β the lincomb locates the point P.
Trisection formulas
If P is the point of trisection of segment AB nearest A then segment AP is 1/3 the length of AB. Equivalently, AB is three times as long as AB. Therefore, 3AP = AB. Hence 3(p -- a) = b -- a. Solving for 3p, 3p = 2a + b. Division of both sides by 3 produces p equal to the first fraction of
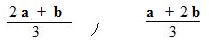 The position vector q equal to the second fraction can be derived from 3QB = AB.
The position vector q equal to the second fraction can be derived from 3QB = AB.
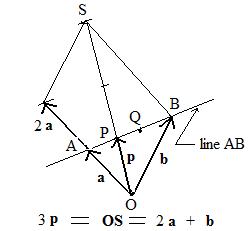
The geometric interpretations of the fractions is interesting. See adjacent figure for locating the point P nearest A on line AB. The vectors 2a and b are added together to get a parallelogram OBS+. The diagonal vector OS = 2a + b. The segment OS passes through P and is 3 times as long as OP. Therefore OS = 3p = numerator of the first fraction. Therefore, p locates P which is the point of trisection nearest A. It is possible to create a similar figure to show that 3q = numerator of the second fraction.
Solution of linear equations involving coefficients
Usually, the unknowns in simultaneous linear equations are denoted by the letters x,y, z, ..... . such as
3x + 2y + z = 3
x + y + z = 2
However, the letters x,y,z denote coordinates in arrays. In discussions involving lincombs, simultaneous linear equations arise from finding values for coefficients. The same equations expressed in the notation for coefficients (Greek letters) are:
3α + 2β + γ = 3
α + β + γ = 2
The method of reducing the number of unknowns will be used here. (Some solutions may be found by use of determinants or matrices. See the volume on matrices.) For example
α + β = 7
α -- β = 5
can be solved by adding the equations together to eliminate β:
2α = 12 therefore α = 6;
Substitution of 6 for α in either equation shows that β = 1
2x2 Determinants and their Values)
The following is a 2x2 determinant with real numbers α, β, γ, δ, and on the right side of the equation is a formula for finding its value, a real number.

The numbers α δ form a product on the main diagonal (\). The numbers β γ form a product on the secondary diagonal (/). The value of the determinant is obtained by the difference of the two products: product on the main diagonal minus the product on the secondary diagonal. As examples, this scheme is used to find the values of the following two determinants:
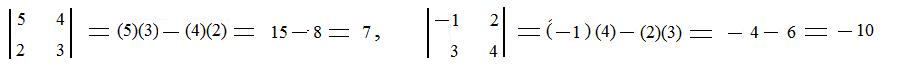
[*] Some useful properties of determinants
(a) If any row has only zeros then the value of the determinant is zero.

(b) If two rows are identical then the value of the determinant is zero.

(c) If two rows are interchanged then the value of the determinant is negated.
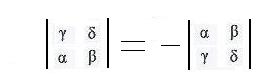
(d) If every number in any row is multiplied by a real number, then the value of the determinant is multiplied by that same number.
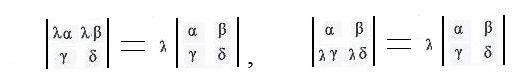
The proofs of parts (a) and (b) are trivial and left to the reader.
The proof of (c) is based on the identity γ β -- δ α = -- (α δ -- β γ).
The first equation of (d) is based on the identity λ α δ -- λ β γ = λ (α δ -- β γ).
The second equation of (d) is based on the identity α λ δ -- β λ γ = λ (α δ -- β γ).