Go to other chapters or to other books of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Chapter 2
Unit Circle
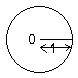 Setwise the unit circle here is a subset of the complex numbers. Geometrically its center is at the origin where the real and imaginary axes intersect. It has a radius of 1. Algebraicly a complex number is on this circle if and only if the absolute value = 1. This circle has interesting yet simple properties: algebraic, geometric and trigonometric to be discussed in this chapter.
Setwise the unit circle here is a subset of the complex numbers. Geometrically its center is at the origin where the real and imaginary axes intersect. It has a radius of 1. Algebraicly a complex number is on this circle if and only if the absolute value = 1. This circle has interesting yet simple properties: algebraic, geometric and trigonometric to be discussed in this chapter.
Examples of unit complex numbers: i, -1, (1 + i)/21/2, where 21/2 is the square root of 2
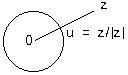 Except for zero, any complex number z can be converted to a unit complex number by dividing it by its absolute value. z/|z| has length 1 because its absolute value = |z|/|z| = 1. This process of dividing a complex number by its absolute value is called normalizing the complex number. Let u = z/|z| be the unit complex number. Geometrically u is obtained by sliding the point along half-line 0z onto the point, where the line segment 0z intersects the circle. See adjacent figure.
Except for zero, any complex number z can be converted to a unit complex number by dividing it by its absolute value. z/|z| has length 1 because its absolute value = |z|/|z| = 1. This process of dividing a complex number by its absolute value is called normalizing the complex number. Let u = z/|z| be the unit complex number. Geometrically u is obtained by sliding the point along half-line 0z onto the point, where the line segment 0z intersects the circle. See adjacent figure.
Intuitively speaking, the unit vector indicates a direction. Two complex numbers have the same direction if their unit vectors coincide. Similar statements exist for opposite directions, at right angles,... etc.
An important theorem discussed in a file in Chapter 1 is the following: the absolute value of a product of complex numbers is the product of their individual absolute values: |zw| = |z||w|. It is obvious then that the product of unit complex numbers is a unit complex number, because for the lengths involved 1 = (1)(1).
The absolute value of the (multiplicative) inverse of a complex number (not zero) is the inverse of the absolute value of that complex number: |1/z| = 1/|z|. For the exercise indicating a proof click here. This means that the inverse of a unit complex number is again a unit complex number because for the lengths involved 1 = 1/1.
This is enough to guarantee that the unit circle is a multiplicative subgroup of the multiplicative system of complex numbers, a term used in modern algebra.
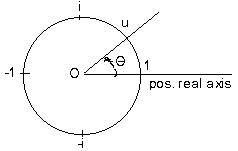 In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the axis. An angle θ can be measured from the positive real axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the axis. An angle θ can be measured from the positive real axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
The central angle θ needs to have measurement. A natural measure of the angle is to compare the arc from 1 to u to the entire circumference of the circle. For example, in the figure θ appears to be about 1/8 of the entire circle. Therefore θ = 1/8 rev. If u moves to the top of the circle (u = i) then θ = 1/4 rev = right angle. If θ = 1/2 then u = -1 and θ is a straight angle. If u starts at 1 and goes around the entire circle three times then θ = 3 rev. The system of measuring in revolutions is useful for indicating speed of an engine, so many revolutions per minute.
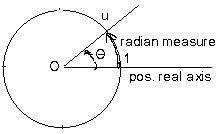 Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
The most common measurement of an angle is with degrees. The number of degrees in 1 revolution has been defined as 360. (Perhaps related to the number 365 days in a year.) If θ is a right angle then &theta = 90°. For a straight angle, θ = 180°. Click here for a more detailed discussion of angles and the various measurements of them
Starting from the positive real axis the central angle θ completely and uniquely determines the half-line 0u, and hence the unit complex number u. The equation u = cis θ expresses this relationship. (The abbreviation cis will be explained later.) Do not confuse cis with cos, which is a common trigonometric function.
Examples: cis 0 = 1, cis 90° = i, cis -90° = -i, cis π = -1, cis 3π/2 = -i, cis (2 rev) = 1, cis 1350° = -i.
The last equality is true because -i = cis 270° and 270 + 3 revolutions = 270 + 3(360) = 1350.
In general cis θ = cis φ if θ - φ = some number of whole revolutions. Click here for a discussion of angles and the various measurements of them.
As mentioned above, any non-zero complex number z can be normalizied and written in the form z = |z| u where u is a point on the unit circle. This unit complex number u = cis θ for some central angle θ. Therefore, z can be written in a polar form: z = r cis θ where r is a real number and r = |z| .
For a short discussion of another expression eiθ that is also a unit vector equal to cis θ, click here
The product of unit vectors has an interesting relationship with cis.
Theorem (de Moivre) For any angles (real numbers) θ and φ,
cis(θ + φ) = (cis θ)(cis φ).
Intuitively speaking cis converts a sum of angles into a product of cis's of those angles. This sounds similar to the law of exponents: ez+w = ezew. Assuming the relation cis ω = eiω:
cis (θ+φ) = eiθ+iφ = eiθeiφ = (cis θ)(cis φ).
This is not a genuine proof of the theorem, because the number e has not been defined and the relation eiω = cis ω has not been proven. (The proof of that relation involving a complex number as exponent is beyond the scope of these notes.) However, a proof using congruent triangles can be seen by clicking here
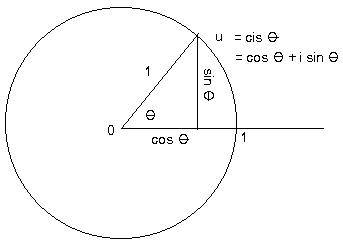 The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ:
The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ:
cis θ = cos θ + i sin θ
This identity explains the abbreviation cis.
But cis θ is a unit complex number. Then the sum of the squares of its real and imaginary coefficients must equal 1. The identity cos² θ + sin² θ = 1 is a well known trigonometric identity.
The familiar trigonometric identities
(#) cos(θ + φ) = cos θ cos φ - sin θ sin φ
(##) sin(θ + φ) = sin θ cos φ + cos θ sin φ
can be proven using the DeMoivre theorem:
($) cos(θ + φ) + i sin(θ + φ) =
cis(θ + φ) = [DeMoivre's theorem used here]
(cis θ)(cis φ) =
(cos θ + i sin θ)(cos φ + i sin φ) =
($$) (cos θ cos φ - sin θ sin φ) + i (sin θ cos φ + cos θ sin φ).
Equating the coefficients of the real parts of ($) and ($$) gives (#). Equating the coefficients of the imaginary parts of ($) and ($$) gives (##).
 click here
eiθ xyz φ 51/2
click here
eiθ xyz φ 51/2
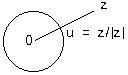 Except for zero, any complex number z can be converted to a unit complex number by dividing it by its absolute value. z/|z| has length 1 because its absolute value = |z|/|z| = 1. This process of dividing a complex number by its absolute value is called normalizing the complex number. Let u = z/|z| be the unit complex number. Geometrically u is obtained by sliding the point along half-line 0z onto the point, where the line segment 0z intersects the circle. See adjacent figure.
Except for zero, any complex number z can be converted to a unit complex number by dividing it by its absolute value. z/|z| has length 1 because its absolute value = |z|/|z| = 1. This process of dividing a complex number by its absolute value is called normalizing the complex number. Let u = z/|z| be the unit complex number. Geometrically u is obtained by sliding the point along half-line 0z onto the point, where the line segment 0z intersects the circle. See adjacent figure.
 Setwise the unit circle here is a subset of the complex numbers. Geometrically its center is at the origin where the real and imaginary axes intersect. It has a radius of 1. Algebraicly a complex number is on this circle if and only if the absolute value = 1. This circle has interesting yet simple properties: algebraic, geometric and trigonometric to be discussed in this chapter.
Setwise the unit circle here is a subset of the complex numbers. Geometrically its center is at the origin where the real and imaginary axes intersect. It has a radius of 1. Algebraicly a complex number is on this circle if and only if the absolute value = 1. This circle has interesting yet simple properties: algebraic, geometric and trigonometric to be discussed in this chapter.
 In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the axis. An angle θ can be measured from the positive real axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the axis. An angle θ can be measured from the positive real axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
 Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
 The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ:
The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ: click here
eiθ xyz φ 51/2
click here
eiθ xyz φ 51/2