 The the following discussions are not proofs that i² must be assigned the value -1, but to make it seem the logical choice.
The the following discussions are not proofs that i² must be assigned the value -1, but to make it seem the logical choice.
Another way of saying all this is:
A complex number is zero if and only if the coefficients of the real and imaginary parts are zero
for any complex number x + y i, if x + y i = 0, then both x=0 and y=0.
From one (complex number) equation x + y i = 0, we can get two (real number) equations x=0 and y=0.
It is easy to show that two complex numbers are equal if and only if the coefficients of their real parts are equal and the coefficients of their imaginary parts are equal. For the exercise click
here.
 The the following discussions are not proofs that i² must be assigned the value -1, but to make it seem the logical choice.
The the following discussions are not proofs that i² must be assigned the value -1, but to make it seem the logical choice.
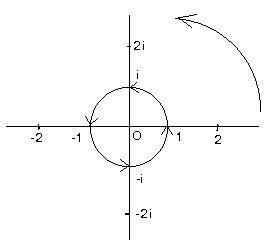
This rotation affects the entire complex plane. Click here to see the exercise with hints to support the statement about this rotation.
======================
(I)(U + V)(X + Y) = UX + VX + UY + VY for any numbers U,V,X,Y
(II)The difference of the squares of two numbers is equal to their sum times their difference: U² - V² = (U + V)(U - V)
(III)If a product of numbers is zero then one or more of the numbers must be zero: if UV=0 then U=0 or V=0 or both
(IV)Every number U not zero has a multiplicative inverse (reciprocal) 1/U
(V)|i²| = |i||i| (product of absolute values, to be confirmed later after i² is given a value)
(VI)U + Vi = X + Yi if and only if U=X and V=Y (here U,V,X,Y must be real numbers)
These statements (I),(II),(III),(IV) are extensions from the real number system. However, they are used here without proof to derive the value of i² in the complex number system.
It is desirable that i² be somewhere in the complex number system. Therefore, there are real numbers x and y such that
(*) i² = x + y i.
By ((IV) i must have a reciprocal 1/i. Multiplying both sides of equation (*) by this reciprocal, the following is obtained:
i = x/i + y
There is no real part on the left side. Set y=0 to simplify the right side and then multiply both sides by i to get:
i² = x.
This suggests that i² is equal to some real number.
Now to narrow down the possible location of i².
Let d (and therefore d²) be any real number. Then by (II)
d² - i² = (d + i)(d - i)
Then d² - i² cannot be zero, because then the right side implies i=d or i=-d, which says that i is real. But i is imaginary. As a result, i² cannot be any positive real number d². In summary, i² must be some negative real number.
Every real number x has an absolute value |x| This can be extended to any complex number |x + y i| = square root of the quantity (x² + y²). If x=0 and y=1, then the expressions reduce to
|i| = 1.
But by (V)
|i²| = |i||i| = (1)(1) = 1.
The only number on the negative real axis with absolute value = 1 is -1.
This suggests i² be given the value -1.
If θ is any real number (or in radians) it can be shown that eiθ is a unit complex number. Moreover, that unit complex number is the same as cis θ:
eiθ = cis θ.
Let θ = π radians. then the expression becomes:
(*) eiπ = -1
because cis π = -1. The contents of expression (*) involves some interesting numbers. e is a constant useful in calculus, i is the imaginary unit, π = 3.14159... is another constant used in geometry to compare the circumference and diameter of circles, and -1 is the first negative integer.
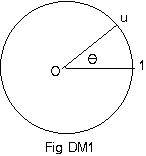
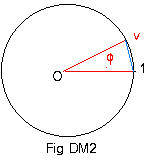
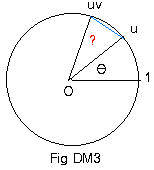
Let u and v be unit complex numbers with central angles θ and φ. (See Fig DM1 and Fig DM2.). Their product uv is also a unit complex number, and is somewhere on the unit circle. (See Fig DM3.)
Now locate a unit complex number w that has central angle θ + φ: w = cis(θ + φ).
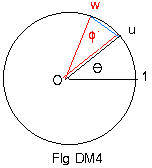
The plan here is to show that points uv and w coincide. (Fig DM3 and Fig DM4.)
Length of chord u,uv
= |uv - u| = |u(v - 1)| = |u||v - 1| = 1|v - 1| = |v - 1|
= length of chord 1,v (Fig DM2) = chord u,w (Fig DM4).
This means that arc u,w in Fig DM4 is congruent to arc u,uv in Fig DM3. Therefore the central angle ? in Fig DM3 must equal the central angle φ in Fig DM4.
Therefore, cis (θ + φ) = w = uv = (cis θ)(cis φ).