Chapter 3
Number Systems: Integers and Non-Negative Integers

Section 1  Attaching Zero to The Natural Numbers

A natural number has been used to represent the number of objects in a bag. But in reality, a bag may be empty, no object is in it. The system of natural numbers is not adequate to represent this situation. The number zero (0) is invented to do that. It is a new number to be "attached" to the system of natural numbers. This new system might be called natural numbers with zero. The more common term for this same system is   the system of non-negative integers. (A later discussion about integers will show the reason for this last terminology.) The symbol N0 (read N zero) may be used in this chapter to mean this expanded system. The following is a list of a first part of N0:

[1.1]
N0 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,...}

This shows that zero is less than any natural number, and is the smallest non-negative integer. In this chapter u,v,w will be used often to represent non-negative numbers.

Addition for the natural numbers was discussed in the previous chapter. Therefore, two non-negative integers not zero may "use" that same addition. The following completes the extension of that addition to all the non-negative integers N0. The use of numbers of objects in a bag and additions of objects reveals the unique manner that zero is involved with addition. If 5 objects are added to an empty bag, then will the bag will hold 5 objects. If w objects are added to an empty bag, then the bag will contain w objects. Similarly, if no objects are added to a bag with w objects then the bag will still hold w objects. These statements may be expressed by the following equations:

[1.2] (Zero is the additive identity*) For any non-negative integer w,

Another is the dual already mentioned in the previous chapter:

[1.3] (One (or unity) is the multiplicative identity*) For any non-negative integer n,

Although a more rigorous proof can be given later using integers and the distributive law, an argument supporting this fact can be given here. If n is any natural number then 1 x n = n. One n appears. It is reasonable that for 1 x 0 = 0, a single zero appears. Commutativity supports 0 x 1 = 0.

Section 2  Introducing Zero to Expand the Natural Numbers

Many of the statements made about natural numbers carry over to the non-negative integers. Like [1.3] some will need modifications or arguments about how zero is involved, since it is not a natural number. For example, using only natural numbers, the sum of natural numbers is greater than any of its parts. But if parts can be zero, this statement must be modified for non-negative integers.

[2.1a] The sum of non-negative integers may be greater than or equal to any of its parts.

[2.1b]* For non-negative integers u and v,    u is less than or equal to v   if and only if    there exists a non-negative integer x such that v = u + x.
Notation: u <= v.

Zero has an effect upon multiplication. By definition of multiplication nw = w + w + ... + w, where n is a natural number and n w's are involved in the addition process. Extend this idea to the natural numbers with zero. If n = 0, no w's are involved, so the product 0w = 0. This intuitive statement is supported by a simple use of a distributive law, (0 + 0)w = 0w + 0w. But 0 + 0 = 0. Therefore 0w = 0w + 0w. Subtract 0w from both sides to get 0 = 0w.

[2.2a] (zero coefficient*) Any product with zero is always equal to zero.

[2.2b] (zero exponent*) Any non-zero quantity with exponent zero is always equal to 1.

Zero raised to the zero power will be discussed later.
Addition by zero is never a problem. But multiplication can be a problem. The equation 2x = 10 can be solved (x = 5), and so can 3x = 0 be solved (x=0). When the coefficient is zero, that is when the problem happens. The equation 0x = 5 cannot be solved. It contradicts [2.2a]. The solution is undefined. The equation 0x = 0 is the other extreme. It has every number as a solution. It is called indeterminate. The following is a result of these situations:

[2.3] (Oddities of zero)
  (a) Zero cannot be the denominator of a fraction
  (b) Zero cannot be a factor of any non-zero number
  (c) Zero is a multiple of every number   (d) A quantity raised to the zero power is equal to 1, unless the quantity itself is equal to zero. Zero raised to the zero power does not exist.

An important fact but often not noticed is the following about a product equal to zero.

[2.4] (*) If a product of numbers is equal to zero, then one or more factors is zero.    uv = 0 implies u=0 or v=0 (or both).

Suppose uv = 0, where u and v are non-negative integers. If v=0, then one of the factors of uv is already zero. The argument is complete.
Suppose v is not zero. Then v is a positive integer. Multiply all non-negative integers [1.1] by v:

Using math induction a more rigorous proof of [2.4] can be created. It can also be proved using the distributive law for subtraction.

If a product of two or more non-zero numbers is zero, then those numbers are called divisors of zero. The statement [2.4] means that the system of non-negative integers has no divisors of zero. Later there will be shown some "strange" number systems with divisors of zero.


If each number in the list of non-negative integers is multiplied by 10, then a list of (non-negative) multiples of 10 is obtained:

If the fraction 43/10 is made, something can be done with non-negative integers. Divide 10 into 43 to get a quotient 4. There is a remainder 3. This can be written 43 = (4)10 + 3. Notice that 40 = 4(10) + 0. 10 is a factor of 40, so the remainder=0.

A collection of 43 objects may be arranged in 4 rows of 10 objects each and there will be 3 objects left over. Click here for another example of division by 10.

In general, given the fraction b/a, divide a into b as far as possible producing a quotient that is a non-negative integer q. Left over will be a remainder r. The remainder is correct if r < a. Then:

[2.5] (The division algorithm) For any non-negative integer b and any natural number a there exist unique non-negative integers q and r such that b = (q)a+ r     where r is a non-negative integer less than a.

Fractions and decimals have not been discussed yet. They are not part of the system of non-negative integers. Intuitively speaking, the fraction b/a is "illegal" in the system of non-negative integers. Yet, for clarity with the readers knowledge it is appropriate to violate this order of presentation.

The reader can verify the following:
   fraction   quotient    remainder        verification:  b = (quotient) x a + remainder
       47/5           9                 2            verification:   47 = (9) x 5 + 2
       200/55       3                35
       43/10         4                3
       30/6          5                 0            6 is a factor of 30
       16/28        0                28
       13/0          cannot compute

In spite of the limitations of the system of non-negative integers,the division algorithm has many applications.

The third example above can be generalized: the remainder after applying the algorithm [2.5] to n/10 produces the last digit of n. Here denominator a = 10. To what is a equal so that the remainder = the last two digits of n?

In section 1 the finite sets of the first n natural numbers were introduced. For example, the collection of the first ten natural numbers N₁₀ = {1,2,3,4,5,6,7,8,9,10}. If the largest natural number in that collection is replaced by zero, then a new collection J₁₀ = {0,1,2,3,4,5,6,7,8,9} of non-negative integers is obtained. It contains the first ten non-negative integers. Similarly,

[2.6] The integers mod n are the first n non-negative integers.

Notice that the natural number n (or anything larger) is NOT in J_n.

The remainders from the fractions 90/10, 531/10, 22/10, 113/10, 64/10, 5555/10, 16/10, 567/10, 98/10, 269/10 form the collection J₁₀ = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} of integers mod 10. By choosing different non-negative values for b, it is possible to do something similar for b/n to get all the numbers in J_n (for any natural number n > 1).

[2.7]* (Remainders of the division algorithm) For any non-negative integer b and any natural number n, the remainder of the fraction b/n is always in the collection J_n of non-negative integers mod n.

The proof for this statement is not given in these discussions. The well ordering princlple can be used in that proof.

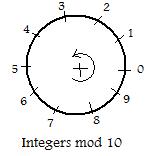The non-negative integers N0 fit on an infinite straight line (more exactly on a half-line). The integers mod n J_n fit on a circle. In the figure to the right the numbers in J₁₀ have been placed around a circle. This figure can be used to find the "sum" of any pair of numbers in J₁₀ back in J₁₀ (Closure under "addition".) To find the sum 9 + 2 Start at 9, and go two markers in the + circular direction (counter-clockwise). The result is 1.To find 8 + 4, start at 8 and go 4 markers in the counter-clockwise direction to get 2.The reader may use the figure to verify the following equations:

The statement [2.7] and the methods just discussed show that it is possible to "add" two numbers in J₁₀ and get a number back in J₁₀. The addition is called mod 10 addition. It is different from ordinary addition of numbers.

It is easy to generalize the situation. For any natural number n it is possible to spread the numbers 0,1,2,...,n-1 evenly around a circle in a counter-clockwise manner.

[2.8a] (mod n addition and multiplication*) The mod n sum of any numbers in J_n is the remainder of the fraction sum/n. The mod n product of any numbers in J_n is defined similarly: the remainder of the fraction product/n.
Notations: u +v = w (mod n),     uv = w (mod n).

The mod 10 sum and product of 9 and 8 are the remainders 7 and 2 of the fractions 17/10 and 72/10, respectively. In the above notation, 9 + 8 = 7 (mod 10)     and     9 x 8 = 2 (mod 10).

The non-negative integers 43 and 183 leave the same number 3 when divided by 10. Also 25 and 17 both leave the remainder 1 when divided by 4. The notation above can be used to express equivalences:    43 = 183 (mod 10)    and 25 = 17 (mod 4).

[2.8b] (mod n equivalence*) Two numbers are equivalent mod n iff they leave the same remainder when divided by n.

Notation: u = v (mod n). Sometimes the (mod n) may be omitted when there is no confusiion with ordinary arithmetic.

It is easy to see that 0, 10, 20, 30, 100, 110, 1000, and any multiple of 10 are equivalent to 0 (mod 10).
In general, any multiple of n is equivalent to 0 (mod n). In J_n, mn = 0 (mod n).

The mod systems J_n (n>1) with their peculiar equivalences, additions and multiplications provide some interesting algebraic properties and will appear in some future sections and throughout modern algebra. J_n under addition and multiplication obey the three laws: they are commutative, associative and distributive. However, for some composite natural numbers n there are zero divisors in J_n. For example, in J₆, 4x3 = 0 (mod 6) because 4x3 = 12 and the fraction 12/6 has a zero remainder (see [2.8a]). Click here for more discussion of the mod systems J_n.