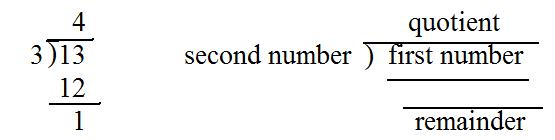
[AM01](*) If p is a (positive) prime then the system Jp of integers mod p has no divisors of zero.
Let u and v be any non-zero numbers in Jp. Looking at the complete factorization of u, v and the product uv, p cannot be a factor of u and p cannot be a factor of v then p cannot be a factor of the product uv. Therefore uv cannot be equivalent to zero.
If n is a natural number and is not a prime then it is composite and there is a product hk = n. Then in Jn the numbers h and k are divisors of zero. In particular in J6, 3 and 2 are divisors of zero, because 3 x 2 = 6 which is equivalent to 0 (mod 6).
(Lemma1) Let n be any natural number. The only non-negative integer h satisfying nh < n is h=0.
PART A:
First n0 = 0 < n. So h=0 is a solution for nh < n.
PART B: (Intuitive argument) nh < n is false for all natural number values for h
For h=1, n1 < n is false.
Suppose h>1.
Then nh = n + n + ... + n, where n appears h times. But a sum of natural numbers is larger than any of those natural numbers.
Therefore nh > n.
Hence for all natural number values for h, nh < n is false.
PART B': (Using math induction) nh < n is false for all natural number values for h
Trivially, for h=1, nh = n. So nh < n is false for h=1.
Suppose nh < n is false for some h>1. This means that nh>n
Recall the theorem that says that the sum of two natural numbers is larger than either number.
So nh + n > n.
Therefore, n(h+1) = nh + n > n + n >n. This means that n(h+1) > n.
So n(h+1) < n is false.
Not all ratios of non-negative integers can be calculated using only non-negative integers.
Example1: ratio 20/6 is not equal to any non-negative integer. The multiples of 6 less than 20 are:
It is important to notice that the multiple must be the largest of all the multiples less than or equal to the given number (20 and 31).
The form 20 = 6(3) + 2 is the form of the division algorithm for the ratio 20/6. Similarly, 33 = 4(7) + 5 is the form of the division algorithm for the ratio 33/7.
The form of the division algorithm for the ratio 20/4 is 20 = 4(5) + 0. The + 0 is not needed.
For the ratio 598/0 there is no form of the division algorithm, because there is no multiple of 0 near or equal to 598. For no ratio with zero denominator is there a form of the division algorithm.
(Division algorithm) For any pair of non-negative integers m,n (but n >0) the form of the division algorithm for the ratio m/n is the equation m = nq + r, where q and r are non-negative integers and 0 < r < n.
m is called the numeraator of the ratio, n is the denominator of the ratio. Also q is the quotient and r is the remainder of the form of the division algorithm.
The remainder is always a non negative integer less than the denominator.
The reaminder may equal zero. In that case, the quotient is a factor of the numerator and the ratio is actually a non-negative integer
The remainder is always less than the denominator. This is a guarantee that the minimum nearness of the multiple of the bottom number to the top number of the ratio. But this also means that the denominator cannot be zero itself.
[**] (Division algorithm) For any non-negative integer m and natural number n, there exist non-negative integers q and r satisfying
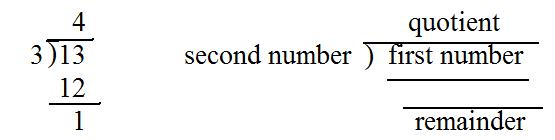
(Division algorithm - informal definition) For any non-negative integer and any natural number ,
Examples:
For 13 and 3, 13 = 3(4) + 1.
For 19 and 5, 19 = 5(3) + 4.
For 3 and 5, 3 = 5(0) + 3.
For 8 and 4, 8 = 4(2) + 0.
The remainder r = 0 if and only if the natural number n is a factor of the non-negative integer m.
The reader can verify the following:
m/n quotient remainder
verification: m = (quotient)n + remainder
47/5
9
2 verification: 47 = (9) x 5 + 2
200/55
3
35
43/10
4
3
30/6
5
0
6 is a factor of 30
16/28
0
28
13/0
cannot compute
Part A: Supporting argument for the division algorithm excluding uniqueness of quotient and remainder.
The geometric interpretation of the division algorithm shows m to lie between two multiples of n, or a multiple of n is equal to m. The set of multiples of n are
Suppose there are possibly two quotients, q1, q2 and possibly two remainders r1, r2. Arrange the notation so that r2 > r1. Then there are possibly two equations for the division algorithm with the same given numbers m and n: