Go to other chapters or to other volumes of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer Programs for this Chapter
Return to index of all chapters in this volume
Volume B Chapter 2
Non-negative Integers
Statements with an asterisk (*) will be generalized in later sections to apply to larger systems of numbers. The associative, commutative and distributive laws are assumed to be true for the system discussed in this section.
It is an interesting fact that the system of Roman numerals did not contain a symbol for zero. But zero will play significant roles in many discussions below and in future volumes.
It is necessary to have a symbol to indicate nothing, 0, called zero. For example, an empty bag has 0 objects in it. Zero is a new number to be "attached" to the set of natural numbers. The set N0 of non-negative integers is the union of zero and the set N of natural numbers.
N0 = {0} ∪ N = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,...
}
The position of zero in set N0 indicates that zero will be less than any natural number, and is the smallest non-negative integer.
Since the set N is a subset of the set N0 (N ⊂ N0), many of the laws and operations on natural numbers may be extended to non-negative integers.
Section 1: Addition of non-negative integers
It is easy to extend the addition operation on N to an addition operation on N0. The addition of natural numbers was discussed in the previous chapter. There remains only to determine addition involving zero. The following does this:
[1.1] (Additive identity*) Any sum of a non-negative integer and zero remains the same if zero is removed from the sum.
For any non-negative integer n, 0 + n = n and n + 0 = n.
This shows how zero fits into the system of addition of non-negative integers. So [1.1] may be considered a definition.
There are three important results from [1.1]. First, is
[1.2] (Closure under addition) The sum of any pair of non-negative integers is a non-negative integer.
Notation: if m,n are non-negative integers, then their sum m + n is a non-negative integer.
The second result is an extension of subtraction. It is now possible to subtract a natural number from itself.
(Subtraction) Any non-negative number subtracted from itself is zero.
Notation: for any non-negative integer n, n - n = 0.
[1.3] (Additive identity is unique) There is only one additive identity, 0.
Notation: if n + x = n for any non-negative integer n, then x = 0.
The argument supporting [1.3] is a simple evaluation of an expression two ways.
Suppose 0' is also an additive identity for the non-negative integers. Then the sum 0 + 0' can be evealuated two ways:
0 + 0' = 0' [using 0 as an additive identity]
0 + 0' = 0 [using 0' as an additive identity]
Therefore 0' = 0 because both are equal to the same expression 0 + 0'.
The fact that addition of natural numbers is commutative and [1.1] together support the following:
[1.4] (Addition is commutative) The sum of two non-negative integers is the same no matter what the order of the numbers is.
Notation: For any non-negative integers m,n, m + n = n + m.
The proof consists of three parts.
Part I: m,n are both natural numbers. The commutive law for natural numbers was discussed in the previous chapter 1.
Part II: m=0. m + n = 0 + n = n = n + 0 = n + m
Part III: n=0. m + n = m + 0 = m = 0 + m = n + m.
The fact that addition of natural numbers is associative and [1.1] together imply:
[1.5] (Addition is associative) For the sum of three non-negative integers, either addition may be done first.
Notation: For any non-negative integers k,m,n, k + (m + n) = (k + m) + n.
The proof consists of four parts.
Part I: k,m,n are all natural numbers. The associative for natural numbers was discussed in the previous chapter 1.
Part II: k=0. k + (m + n) = 0 + (m + n) = m + n = (0 + m) + n = (k + m) + n.
Part III: m=0. k + (0 + n) = ... = (k + 0) + n.
Part IV: n=0. k + (m + 0) = ... = (k + m) + 0.
The associative law allows the definition of the addition of three non-negative integers without parentheses: k + m + n.
The statements [1.4] and [1.5] combine to support
[1.6] (Addition in general) The addition of any non-negative numbers may be done in any order
Notation (for three numbers): k + m + n = k + n + m = m + k + n = m + n + k = n + k + m = n + m + k.
For h number of non-negative integers, there are h! (factorial) sums of the numbers in different orders. (Factorials were discussed briefly in Chapter on permutations in Volume B.)
Section 2: Multiplication of non-negative integers
The next task is to extend the operation of multiplication to the non-negative integers. Many of the statements about multiplication of natural numbers were presented as duals of statements about addition of natural numbers. Therefore, many of the following statements are duals of statements about addition of non-negative integers. Therefore, it is desirable that the commutative, associative and distributive laws be true for non-negative integers. The following is the dual of [1.1]:
[2.1] (Multiplicative identity*) For any non-negative integer n,
1⋅n = n and n⋅1 = n.
[2.2] (Multiplicative identity is unique) There is only one multiplicative identity, 1.
Notation: if nx=n for all nonnegative integers n, then x=1.
Suppose 1' is also a multiplicative identity for the non-negative integers. Then the product (1)(1') can be evealuated two ways:
(1)(1') = 1' [using 1 as a multiplicative identity]
(1)(1') = 1 [using 1' as a multiplicative identity]
Therefore 1' = 1 because both are equal to the same expression (1)(1').
In order to extend some laws about multiplication of natural numbers to non-negative integers, it is necessary sometimes to focus attention on the behavior of zero when multiplying non-negative integers. There is no duality here.
It is already known that the product of a natural number and zero is equal to zero: n0 = 0. Algebra and geometry provide motivation for this equation.
Simply add n zeros together: 0 + 0 + ... + 0 = 0.
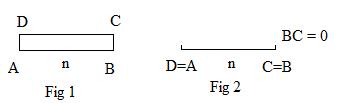 Consider the rectangles in the adjacent figures where AB = n. In Fig 1 the area of the rectangle is length x height = AB x BC = n x BC. Now let vertical sides BC and AD shrink to zero, so that roof DC collapses onto floor AB in Fig 2. Hence BC=0. Then 0 = area = AB x 0 = n0.
Consider the rectangles in the adjacent figures where AB = n. In Fig 1 the area of the rectangle is length x height = AB x BC = n x BC. Now let vertical sides BC and AD shrink to zero, so that roof DC collapses onto floor AB in Fig 2. Hence BC=0. Then 0 = area = AB x 0 = n0.
The following and its proof extends the idea to non-negative integers:
[2.3] (Multiplication by zero*) Any product involving zero and non-negative integers is zero.
Notation: For any non-negative integer n, n0 = 0 and 0n = 0.
In order that the two-sided distributative law hold for non-negative integers, it is necessary that
(0 + 0)n = 0n + 0n, n(0 + 0) = n0 + n0 for any non-negative integer n
But 0 + 0 = 0. So these two equations reduce to
0n = 0n + 0n, n0 = n0 + n0
Subtracting 0n and n0 from these quations respectively produces
0 = 0n, 0 = n0
Actually [1.7] is sufficient to ensure that the two-sided distributive law holds for non-negative integers if it already holds for natural numbers.
[2.4] (Closure under multiplication) The product of any non-negative integers is a non-negative integer.
Notation: if m,n are non-negative integers, then their product mn is a non-negative integer.
Clearly, [2.4] is the dual of [1.2]. Some of the following about multiplication are duals of above statements about addition.
The fact that multiplication of natural numbers is commutative and [2.3] together imply:
[2.5] (Multiplication is commutative) The product of two non-negative integers is the same no matter what the order of the numbers is.
Notation: For any non-negative integers m,n, mn = nm.
The proof consists of two parts.
Part I: m,n are both natural numbers. The commuttive laws for natural numbers were discussed in the previous chapter 1.
Part II: m=0 or n=0. mn = 0 = nm (by 2.3).
The fact that multiplication of natural numbers is associative and [2.3] together imply:
[2.6] (Multiplication is associative) For the product of three non-negative integers, either multiplication may be done first.
Notation: For any non-negative integers k,m,n, k(mn) = (km)n.
The proof consists of four parts. In each part [2.3] is used repeatedly.
Part I: k,m,n are all natural numbers. The associative for natural numbers was discussed in the previous chapter 1.
Part II: k=0. k(mn) = 0(mn) = 0 = 0m = (0m)n = (km)n.
Part III: m=0. k(mn) = k(0n) = k0 = 0 = 0n = (k0)n = (km)n.
Part IV: n=0. k(mn) = k(m0) = k0 = 0 = (km)0 = (km)n.
The associative law allows the definition of the multiplication of three non-negative integers without parentheses: kmn.
The statements [2.5] and [2.6] combine to support
[2.7] (Multiplication in general) The multiplication of any non-negative numbers may be done in any order
Notation (for three numbers): kmn = knm = mkn = mnk = nkm = nmk.
For h number of non-negative integers, there are h! (factorial) products of the numbers in different orders. (Factorials were discussed briefly in Chapter on permutations in Volume B.)
Section 3: Additional properties of non-negative integers
It is desirable that the addition law of exponents (km)n = knmn for natural numbers be extended to exponents with non-negative integers. Again attention is focused on zero exponents. Clearly, for any natural number n,
0n = (0)(0)...(0) [a product of n zeros] = 0
[3.1] (zero exponent*) Any natural number with exponent zero is equal to 1.
Notation: n0 = 1 for any natural number n.
Since k + 0 = k,
nk + 0 = nk
By the law of addition of exponents,
nk + 0 = nkn0
Therefore,
nkn0 = nk
But this means that n0 is acting like a multiplicative identity. But by [1.6] there is only one identity. So n0 = 1.
For any natural number n, both expressions n0 and 0n have meaning. Absent from the above discussion is 00. It turns out that zero raised to the zero power has no meaning and, therefore, is unacceptable. It be discussed later.
Addition by zero is never a problem. But multiplication can be a problem. The equation 2x = 10 can be solved (x = 5), and so can 3x = 0 be solved (x=0). When the coefficient is zero, that is when the problem happens. The expression 0x = 5 cannot be solved. It contradicts [1.7]. No solution exists. The equation 0x = 0 is the other extreme. It has every number as a solution. It is called indeterminate. The following is a result of these situations:
An important fact about a product equal to zero is the following.
[3.2] (No divisors of zero*) If a product of two non-negative integers is equal to zero, then one or both of the numbers must be zero.
Notation: if mn = 0 for non-negative integers m,n, then either m=0 or n=0 (or both).
The contrapositive of this implication is equivalent to the following: the product of two natural numbers is not zero. This is true because of the closure of natural numbers under multiplication - the product of natural numbers is a natural number. Zero is not a natural number. The truth of the contrapositive proves [3.2].
This theorem [3.2] is used in elementary algebra to solve some equations by factoring. to solve the quadratic equation
x2 − 3x + 2 = 0
factor it:
x2 − 3x + 2 = (x − 1)(x − 2)
One or both of the factors must be zero: x − 1 = 0 or x − 2 = 0. Therefore x = 1 or x = 2. Both the numbers 1 and 2 are solutions to the quadratic equation.
If a product of two or more non-zero numbers is zero, then those numbers are called divisors of zero. The statement [3.2] means that the system of non-negative integers has no divisors of zero. In fact, most number systems already familiar to the reader have no divisors of zero. But later there will be discussed some "strange" yet important numerical systems with divisors of zero.
------
Given two non-negative integers it is possible to produce two more non-negative integers from them using the two operations of addition and multiplication of the two numbers: m + n and and mn. The division algorithm, to be discussed here, provides another way to produce the two non-negative integers. It is based on an attempt to divide the second number into the first, using only non-negative integers. But division by zero is not allowed. So the second number must be a natural number. It may be helpful to write the division as a ratio:
(non-negative integer)/(natural number)
even though a discussion of fractions is delayed until Chapter 4. For that reason here it is called a ratio. Then the non-negative integer becomes the numerator and the natural number becomes the denominator of the ratio. (Some people prefer to use the notation
(non-negative integer) : (natural number)
as the symbol for ratio.)
Suppose the two given numbers are 13 and 3. The ratio is the symbol 13/3. Long division has the form
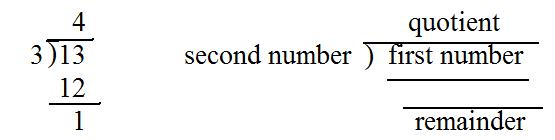 The two numbers produced by the division algorithm are quotient = 4 and remainder = 1. The long division process continues until the remainder is a non-negative integer less than the natural number (denominator).
The two numbers produced by the division algorithm are quotient = 4 and remainder = 1. The long division process continues until the remainder is a non-negative integer less than the natural number (denominator).
Notice that it would be impossible to do the division if the natural number 3 were replaced by zero.
In the following, may the reader think of the given numbers (non-negative integer) and (natural number) as forming a ratio (non-negative integer) / (natural number). The (quotient) and (remainder) are computed by the method of long division shown above. The following is a very important theorem involving non-negative integers. Intuitively speaking, it is an attempt to do division using only non-negative integers and no decimals nor fractions.
[3.4](Division algorithm) For any (non-negative integer) and any (natural number) , there exist unique non-negative integers (quotient) and (remainder) all satisfying
non-negative integer = (natural number)x(quotient) + remainder
The remainder is always less than the (natural number).
Notation: if m is any non-zero integer, and if n is any natural number, then there exist unique non-negative integers q and r such that
m = n(q) + r where 0 < r < n
The inequalities 0 < r < n are an important part of the division algorithm.
The weak inequality 0 < r is redundant, because r must be a non-negative integer.
Click here to see arguments supporting [3.4].
Examples: ratio m/n
For m and n, there exist unique numbers q and r that satisfy m = n(q) + r and 0<r<n.
For 13 and 3, there exist unique numbers 4 and 1 that satisfy 13 = 3(4) + 1 and 0<1<3.
For 19 and 5, there exist unique numbers 3 and 4 that satisfy 19 = 5(3) + 4 and 0<4<5.
For 3 and 5, there exist unique numbers 0 and 3 that satisfy 3 = 5(0) + 3 and 0<3<5.
For 8 and 4, there exist unique numbers 2 and 0 that satisfy 8 = 4(2) + 0 and 0<0<4.
For 7 and 0, there do not exist any non-negative integers q and r that satisfy 7 = 0(q) + r and 0<r<0.
[Notice that 0<0 is not possible.]
For more numerical examples of the division algorithm click here.
For the ratio (non-negative integer)/(natural number):
(a) The natural number is a divisor of the non-negative integer if and only if the remainder = 0.
(b) If the natural number is larger than the non-negative integer then quotient = 0 and remainder = non-negative integer.
 A geometric interpretation may increase understanding
A geometric interpretation may increase understanding
given non-negative integer = 39 and natural number = 9.
39 = 9(4) + 3.
If each number in the set M = N0 of all non-negative integers is multiplied by 9, then an infinite subset M9 of all (non-negative) multiples of 9 is obtained:
M9 = {0,9,18,27,36, 45,54,63,72,81,90,99,...}
39 is between 36 and 45 in the set M9 of multiples of 9. The largest multiple less than 39 is 36. And 39 is 3 beyond that largest multiple 36. This can be seen in the adjacent figure.
Section 4: Integers mod n
Among its many applications the division algorithm allows the creation of new systems of numbers with operations of special addition and special multiplication. Let Jn denote the set of the first n non-negative integers:
Jn = {0,1,2,...,n-1}
Now Jn is a subset of N0 = {0,1,2,...,n,...}. But Jn is not closed under ordinary addition given in [1.2]. The sums of some numbers in the subset are outside that subset J. Also some products are outside the subset. For example, for the specific subset
J6 = {0,1,2,3,4,5}
the ordinary sum 4 + 5 and ordinary product (4)(5) are not in the subset.
But notice that using the division algorithm with the ratios 9/6 and 20/6,
9 = 6(1) + 3 and 20 = 6(3) + 2
the remainders 3 and 2 are back in the subset J6.
In general, if k and m are numbers in Jn then, using the division algorithm, the remainder from the ratio (k+m)/n will be less than n. This means that the remainder is always back in Jn. This fact allows a new type of addition and multiplication, called mod addition and mod multiplication to be defined for Jn.
Notation: k + m mod n.
For any numbers k and m in Jn, k + m mod n = r where r is the remainder from the division algorithm applied to the ratio (k + m)/n.
Subset J6: replace ordinary sums and ordinary products by remainders from the division algorithm for the ratios (sum)/6 = 9/6 and (product)/6 = 20/6. To indicate the special addition and multiplication processes it is customary to attach the word (mod 6):
4 + 5 = 3 (mod 6) and (4)(5) = 2 (mod 6).
[4.1] (Integers mod n) Let n be any natural number and k,m any non-negative integers. The system of integers mod n consists of the set of the first n non-negative integers
Jn = {0,1,2,...,n-1}
with special operations of mod addition and mod multiplication:
k + m (mod n) and km (mod n)
where these are the remainders of the ratios (k + m)/n and (km)/n respectively
The division algorithm guarantees that the remainders are non-negative integers less than n: they are always back in the set Jn. Therefore, this set is closed under the operations of mod addition and mod multiplication.
Click here for more examples of integers mod n and the special operations of addition and multiplication.
The numbers 2 and 3 are in J612. If n has factors k and m, then the product km= 0 mod n. The product is also true if km = any multiple of n. Divisors of zero are undesirable. Thkey are not natural! The following guarant4es no divisors of zero among the system of integers mod n.
[4.2] (No divisors of zero) In the system of integers mod n, there are no divisors of zero if and only if n is prime.
For a discussion supporting [4.2], click here.
====================
In spite of the limitations of the system of non-negative integers,e.g. negative numbers are needed to make subtraction of non-negative integers always possible, the division algorithm has many applications.
The third example above can be generalized: the remainder after applying the algorithm [2.5] to n/10 produces the last digit of n. Here denominator a = 10. To what is a equal so that the remainder = the last two digits of n? (In programming, this suggests a method of stripping off the digits of natural number.)
In section 1 the finite sets of the first n natural numbers were introduced. For example, the collection of the first ten natural numbers N10 = {1,2,3,4,5,6,7,8,9,10}. If the largest natural number in that collection is replaced by zero, then a new collection J10 = {0,1,2,3,4,5,6,7,8,9} of non-negative integers is obtained. It contains the first ten non-negative integers. Similarly,
J4 = {0,1,2,3}, J7 = {0,1,2,3,4,5,6}, J2 = {0,1}, Jn = {0,1,2,... n-1}
[4.3] The integers mod n are the first n non-negative integers.
It is important to notice that the natural number n (or anything larger) is NOT in Jn. Intuitively speaking, the n that would be in Jn has been replaced by zero. To "convert" the collection Nn of the first n natural numbers to JN of integers mod n, replace the n in Nn by zero. Both Nn and Jn have the same number of objects in them, namely n objects."
The remainders from the fractions 90/10, 531/10, 22/10, 113/10, 64/10, 5555/10, 16/10, 567/10, 98/10, 269/10 form the collection J10 = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} of integers mod 10. By choosing different non-negative values for b, it is possible to do something similar for b/n to get all the numbers in Jn (for any natural number n > 1).
[4.4] (Remainders of the division algorithm*)
For any non-negative integer b and any natural number n, the remainder of the fraction b/n is always equivalent to some number in the collection Jn of non-negative integers mod n.
The proof for this statement is not given in these discussions. The well ordering princlple can be used in that proof.
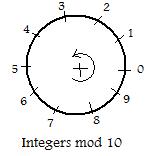 The non-negative integers N0 fit on an infinite straight line (more exactly on a half-line). The integers mod n Jn fit on a circle. In the figure to the right the numbers in J10 have been placed around a circle. This figure can be used to find the "sum" of any pair of numbers in J10 back in J10 (Closure under "addition".) To find the sum 9 + 2 Start at 9, and go two markers in the + circular direction (counter-clockwise). The result is 1.To find 8 + 4, start at 8 and go 4 markers in the counter-clockwise direction to get 2.The reader may use the figure to verify the following equations:
The non-negative integers N0 fit on an infinite straight line (more exactly on a half-line). The integers mod n Jn fit on a circle. In the figure to the right the numbers in J10 have been placed around a circle. This figure can be used to find the "sum" of any pair of numbers in J10 back in J10 (Closure under "addition".) To find the sum 9 + 2 Start at 9, and go two markers in the + circular direction (counter-clockwise). The result is 1.To find 8 + 4, start at 8 and go 4 markers in the counter-clockwise direction to get 2.The reader may use the figure to verify the following equations:
(#) 3 + 2 = 5, 8 + 3 = 1, 7 + 6 = 3, 6 + 4 = 0, 8 + 2 + 3 = 3
The sums may be determined without using the figure. After the sum has been found by ordinary addition (often getting a number too large to be in collection of mod integers) find the remainder of the fraction sum/n In this case n = 10. For the equations in (#) above,
(3 + 2)/10 has the remainder 5, (8 + 3)/10 has the remainder 1, (7 + 6)/10 has the remainder 3,
(6 + 4)/10 has the remainder 0, (8 + 2 + 3)/10 has the remainder 3.
The statement [2.7] and the methods just discussed show that it is possible to "add" two numbers in J10 and get a number back in J10. The addition is called mod 10 addition. It is different from ordinary addition of numbers.
It is easy to generalize the situation. For any natural number n it is possible to spread the numbers 0,1,2,...,n-1 evenly around a circle in a counter-clockwise manner.
[4.5a] (mod n addition and multiplication*)
The mod n sum of any numbers in Jn is the remainder of the fraction sum/n. The mod n product of any numbers in Jn is defined similarly: the remainder of the fraction product/n.
Notations: u +v = w (mod n), uv = w (mod n).
The mod 10 sum and product of 9 and 8 are the remainders 7 and 2 of the fractions 17/10 and 72/10, respectively. In the above notation, 9 + 8 = 7 (mod 10) and 9 x 8 = 2 (mod 10).
The non-negative integers 43 and 183 leave the same number 3 when divided by 10. Also 25 and 17 both leave the remainder 1 when divided by 4. The notation above can be used to express equivalences: 43 = 183 (mod 10) and 25 = 17 (mod 4).
[4.5b] (mod n equivalence*) Two numbers are equivalent mod n iff they leave the same remainder when divided by n.
Notation: u = v (mod n). Sometimes the (mod n) may be omitted when there is no confusion with ordinary arithmetic and n can be remembered.
It is easy to see that 0, 10, 20, 30, 100, 110, 1000, and any multiple of 10 are equivalent to 0 (mod 10).
In general, any multiple of n is equivalent to 0 (mod n). In Jn, mn = 0 (mod n).
The mod systems Jn (n>1) with their peculiar equivalences, additions and multiplications provide some interesting algebraic properties and will appear in some future sections and throughout modern algebra. Jn under addition and multiplication obey the three laws: they are commutative, associative and distributive. However, for some composite natural numbers n there are zero divisors in Jn. For example, in J6, 4x3 = 0 (mod 6) because 4x3 = 12 and the fraction 12/6 has a zero remainder (see [4.5a]). Click here for a further discussion of primes and divisors of zero.
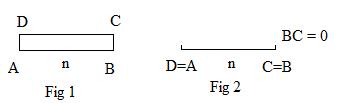 Consider the rectangles in the adjacent figures where AB = n. In Fig 1 the area of the rectangle is length x height = AB x BC = n x BC. Now let vertical sides BC and AD shrink to zero, so that roof DC collapses onto floor AB in Fig 2. Hence BC=0. Then 0 = area = AB x 0 = n0.
Consider the rectangles in the adjacent figures where AB = n. In Fig 1 the area of the rectangle is length x height = AB x BC = n x BC. Now let vertical sides BC and AD shrink to zero, so that roof DC collapses onto floor AB in Fig 2. Hence BC=0. Then 0 = area = AB x 0 = n0.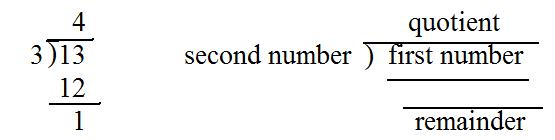
 A geometric interpretation may increase understanding
A geometric interpretation may increase understanding The non-negative integers N0 fit on an infinite straight line (more exactly on a half-line). The integers mod n Jn fit on a circle. In the figure to the right the numbers in J10 have been placed around a circle. This figure can be used to find the "sum" of any pair of numbers in J10 back in J10 (Closure under "addition".) To find the sum 9 + 2 Start at 9, and go two markers in the + circular direction (counter-clockwise). The result is 1.To find 8 + 4, start at 8 and go 4 markers in the counter-clockwise direction to get 2.The reader may use the figure to verify the following equations:
The non-negative integers N0 fit on an infinite straight line (more exactly on a half-line). The integers mod n Jn fit on a circle. In the figure to the right the numbers in J10 have been placed around a circle. This figure can be used to find the "sum" of any pair of numbers in J10 back in J10 (Closure under "addition".) To find the sum 9 + 2 Start at 9, and go two markers in the + circular direction (counter-clockwise). The result is 1.To find 8 + 4, start at 8 and go 4 markers in the counter-clockwise direction to get 2.The reader may use the figure to verify the following equations: