Section 3 The Integers J
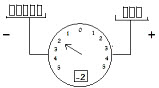 To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
There is another measuring indicator showing numbers in a rectangular window. It also indicates the excess weight (in this case 2). But to indicate which side, a minus sign is attached. A minus sign indicates the left platform, a plus sign indicates the right platform. The integer -2 gives both pieces of information, which platform is heavier and by how much..
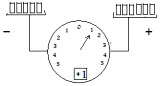 The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
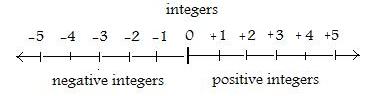 By placing all the weights on one platform and no weights on the other platform the machine converts natural numbers (the weights themselves) into signed integers (as seen in the rectangular window on the scale). After locating a point O (the origin) the integers locate points indicated by vertical markers on the line as shown in the figure to the right. The weights themselves determine how far a marker is from the origin. The integer +4 is the weight 4 on the platform on the right (nothing on the left platform) and 4 is the disstance between the origin and the marker. Similarly -3 is associated with a marker on the left of O. The weight there is 3 (no weights on the right platform) and he distance between the marker and O is 3. Zero 0 and the origin O coincide.
By placing all the weights on one platform and no weights on the other platform the machine converts natural numbers (the weights themselves) into signed integers (as seen in the rectangular window on the scale). After locating a point O (the origin) the integers locate points indicated by vertical markers on the line as shown in the figure to the right. The weights themselves determine how far a marker is from the origin. The integer +4 is the weight 4 on the platform on the right (nothing on the left platform) and 4 is the disstance between the origin and the marker. Similarly -3 is associated with a marker on the left of O. The weight there is 3 (no weights on the right platform) and he distance between the marker and O is 3. Zero 0 and the origin O coincide.
[3.1] (Absolute value - geometric definition) The absolute value of an integer is the distance between the marker located by the integer and the origin O.
Notation: |w| where w is any integer.
Examples: |+4| = 4, |-3| = 3, |0| = 0.
An algebraic definition of absolute value will be given later.
The signs of integers tell onto which platform of the machine to load weights . +4 means to place a weight of 4 on the right platform. -6 means to load a weight of 6 onto the left platform. The machine shows the sum of these in the rectangular window. It will be -2.
The machine gives a physical method for the addition of integers.
To find the sum of +2 and +3, load weights of 2 and 3 onto the right platform, and load nothing onto the left platform. The sum will be +5. Similarly the sum of -2 and -3 will involve the left platform and the sum will be -5. From using the machine the following laws for addition of integers can be determined:
[3.2] (Addition of signed integers)
(a) If two (or more) integers have the same sign, then add their absolute values and take the common sign for the sum.
(b) If two integers have different signs, then subtract their absolute values with the limited subtraction for natural numbers and take the sign of the integer with the larger absolute value.
Theoretically, the machine can produce the sum of any two integers.
[3.3] (Closure of the integers under addition) Any pair of integers may be added, and the sum is always an integer.
The the symbol for addition is the usual plus sign.. It is sometimes necessary to distinguish it from the plus sign used to indicate positive integers. Temporarily it will be written in red (+). For example (-6) + (+4) = -2. (For addition of natural numbers the addition sign should be also in red, but was not necessary until now in this section.)
In previous sections letters could represent natural numbers, for example m=4, n = 5, etc. In this section letters can represent integers, u = +4, v = -5. Then m + n = 9 and u + v = -1. Notice that u and v denote "entire" integers and, therefore, include their signs (+ and -).
The addition of integers shows the net effect of withdrawal and deposit of money to a bank account. If $4 are deposited and then $5 are withdrawn from the same account, the two operations together are equivalent to a withdrawal of $1 from that account.
Zero continues to play the role of an identity.
[3.4] (Additive identity for integers)
For any integer w, w + 0 = w 0 + w = w.
If the sum of two integers is zero, then the two integers have a special relationship.
[3.5a] (Additive inverses*)
If the sum of two integers is zero then each is called the additive inverse of the other.
-4 is the additive inverse of 4, and +5 is the additive inverse of -5. Additive inverses always have the same absolute value, but have opposite signs. Midway between their markers is the origin. The word "inverse" has the idea of undoing or opposing something. Adding -5 to anything is the opposite of adding +5 to it. If a person withdraws $5 from a bank account, that is the opposite of depositing $5 to that account. Withdrawing and then depositing $5 is equivalent to depositing $0 into (or withdrawing $0 from) the account.
[3.5b]To indicate the additive inverse of an integer, a red minus sign will be written before the integer. Therefore, -(+3) = -3. -(-2) = +2. The minus sign in red is different from the minus sign that is part of a negative integer. Because the red minus sign is used to indicate additive inverses, the additive inverses are also called They are also called negatives of each other. When "negative" refers to part of a negative integer, then it is written in black. The meanings of the colors are seen in the true equations -(+3) = -3 -(-4) = +4. In a sense two signs are combined into one sign that is part of an integer. A more formal support for this computation will be given in a later discussion about multiplication of integers. Before a letter a minus sign is red: -w. It means that the additive inverse of w is involved.
Every integer has an additive inverse. Therefore, if an integer and its additive inverse are both listed, then one of them will not be negative (they both may be zero). The absolute value of an integer is itself if the integer is zero or positive, or its additive inverse if the integer is negative. The absolute value |3| is that non negative integer from the pair 3, -3. Also |-4| is that non-negative integer from the pair 4,-4. Also |0| is equal to either non-negative integer from the pair 0,0. An algebraic definition of absolute value may be made from these observations.
[3.6] The integers under addition are one of many algebraic systems. The four properties
(a) closure [3.3]
(b) associative operation [assumed]
(c) there is an identity element [3.4]
(d) every element has an inverse [3.5]
are found in many of those systems, so many, that they are worth collecting to define a category called a group.
The integers under addition have an additional property:
(e) commutativity assumed
Under addition the integers form a commutative group.
The even natural numbers 2N are a system under addition not having properties (c) and (d), satisfying only half of (a),(b),(c),(d). Therefore 2N is called a semi-group. Actually 2N is a commutative semi-group. Since 1 is a natural number, the natural numbers N form a commutative semi-group with unity. (Unity distinguishes the multiplicative identity 1 from the additive identity zero, 0). In later sections there will be shown non-commutative groups and non-commutative semi-groups. They are always written with multiplications as their operations.
The definition [1.13b] of subtraction of natural numbers can be extended literally to integers.
[3.7a] (Standard definition of subtraction)
The difference s-w of two integers s and w is that integer x that satisfies the equation s = w + x.
In anticipation, by ordinary algebra, x = s - w. But it is easily checked that x = s + (-w) is also a solution. (Use the commutative, associative laws and the property of zero in [3.5] and [3.4].). Therefore, an equivalent definition is:
[3.7b] (Alternative definition of subtraction)
The difference s - w of two integers s and w can be calculated from the expression involving addition and the additive inverse: x = s + (-w).
Examples:
(-3) - (+4) = (-3) + (-4) [by [3.7b] and [4.5b]]
= -7 [by [3.2a]]
(-6) - (-2) = (-6) + (+2) [by [3.7b] and [4.5b]]
= -4 [by [3.2b]]
For subtracting a smaller positive integer from a larger positive integer, the limited subtraction of natural numbers is directly involved.
(+7) - (+5) = (+7) + (-5) = +(7 - 5) = (+2) [by [3.2b]].
Similarly, in the addition of two positive integers the addition of natural numbers is involved:
(+7) + (+5) = +(7 + 5) = (+12) [by [3.2a]].
This provides motivation for making the natural numbers part of the integers:
[3.8] If a number, not zero, is written without a sign then it is considered positive.
5 = +5, 8 = +8, 1234 = +1234....
Distinguishing the red (-) and black (+) minus signs is not necessary. for example, -4 = -(+4) = -4. These equalities work for any natural number replacing 4.
9 - 5 = 4 is the same as (+9) - (+5) = (+4).
9 + 5 = 14 is the same as (+9) + (+5) = +14.
This agreement also makes positive integers and zero equal to their own absolute values.
|5| = 5 is the same as |+5| = +5. But |-4| = 4. The - is a subtraction sign . Even written -(+4) this can be considered the subtraction from zero: 0 - (+4).
[3.9] (Algebraic definition of absolute value)
For any integer w, |w| = w if w is positive or zero, and |w| = -w if w is negative.
|4] = 4. Here w = 4 = +4.
|-4| = -(-4) = 4. Here w = -4. The subtraction sign is still needed here to produce the additive inverse of -4.
[3.10] (Products of two signed integers)
Much of the multiplication of integers follows from statements made earlier in discussions of the multiplication of natural numbers and of non-negative integers. There are five possibilities:
(a) If one (or both) of two integers is zero, then their product is zero.
(b) The product of two positive integers is a positive integer.
(c) The product of a positive integer and a negative integer is a negative integer.
(d) The product of a negative integer and a positive integer is a negative integer.
(e) The product of two negative integers is a positive integer.
In the previous section, product of 0 and a non-negative integer was shown to be zero. It is easy to change this argument to include all integers.
Because all natural numbers have been identified with positive integers, (b) has already been discussed in the previous chapter.
In a multiplication of a positive integer and a number (c), the positive integer counts how many times the number appears in the addition of the number to itself. Since the number being repeated is always negative, the sum must be negative. Example, 3(-2) = (-2) + (-2) + (-2) = -6.
In a product of a negative integer and a positive integer (d), the two integers can be interchanged by the commutative law, and the previous statement (c) can be applied to this new arrangement of factors.
Part e needs more of an argument. In algebraic symbols, it says, for any natural numbers m and n, (-m)(-n) = mn . A simple proof is produced by taking an arbitrary negative integer -m and the sum of an arbitrary positive integer n and its additive inverse -n, and form their product:
E = (-m)[n + (-n)]
Expression E can be simplified in two ways;
(1) simplify the expression in the square brackets [ ]:
E = (-m)[0] = 0
(2) using the distributive law multiply (-m) and the two terms of the sum inside the brackets, and then (d):
E = (-m)n + (-m)(-n) = -mn + (-m)(-n)
Since both 0 and -mn + (-m)(-n) are equal to E, they are equal to each other:
E=E: 0 = -mn + (-m)(-n)
Therefore, (-m)(-n) = mn.
The reader may use this same idea of two evaluations but this time using "incomplete" factorings of the expression
mn + m(-n) + (-m)(-n) to prove part (e).
(This method of evaluating a common expression in different ways to get an equality is used in other places in mathematics.)
Because of part (e) the "official" definition of absolute value may be made here.
(Absolute value - algebraic definition) For any integer w, if w is negative then |w| = -w; otherwise |w| = w.
A perfect square is an integer that is equal to a product of some integer with itself. The following is a list of all perfect squares less than 100:
0,1,4,9,16,25,36,49,64,81
Often the word "perfect" is omitted. Parts a, b and (e) of [3.10] guarantee that the square of any integer is never negative. Therefore,
Lemma The absolute value of a perfect square is the perfect square itself: |w2| = w2.
This lemma can be used to prove some equations and inequalities involving absolute values using their squares and simple familiar algebra. The lemma is used to prove two facts in [3.11] below about absolute values of sums and products. These facts and their generalizations (into norms) find use in many places in mathematics.
[3.11] (Absolute values of products and sums)
(a)The absolute value of a product of two integers is equal to the product of their individual absolute values:
|uv| = |u| |v|
(b)The absolute value of a sum of two integers is less than or equal to the sum of their absolute values:
|u + v| <= |u| + |v|.
(This part is called the "triangle inequality" , which says that the length of one side of a triangle is less than the sum of the lengths of the other two sides. This name will have more meaning in the volume on vectors.)
(a) Prove the equality of the squares of both sides.
|uv|2 = (uv)2 = u2v2 = |u|2|v|2
Therefore, |uv|2 = |u|2|v|2
taking the square roots of both sides produces part (a) of [3.11].
(b) Prove the inequality of the squares of both sides and use the fact that no integer is larger than its absolute value:
|u + v|2 = (u + v)2 = u2 + 2uv + v2 <= |u|2 + 2|u||v| + |v|2 = (|u| + |v|)2
Therefore: |u + v|2 <= (|u| + |v|)2. taking square roots of both sides produces the desired inequality.
By definition [3.5a] if the sum of two numbers is zero then the two numbers are additive inverses of each other. It is interesting to apply this definition to the additive integers Jn mod n. The following are zero sums (mod 10 addition) of pairs of numbers in J10 = {0,1,2,3,4,5,6,7,8,9}:
0 + 0 = 0, 1 + 9 = 0, 2 + 8 = 0, 3 + 7 = 0, 4 + 6 = 0 5 + 5 = 0
This means that the following are pairs of additive inverses mod 10:
0 and 0, 1 and 9, 2 and 8, 3 and 7, 4 and 6, 5 and 5.
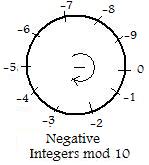 As a reminder of additive inverses, a person could write for J10 with its mod 10 system
As a reminder of additive inverses, a person could write for J10 with its mod 10 system
(#) -0 = 0, -1 = 9, -2 = 8, -3 = 7, -4 = 6, -5 = 5, -6 = 4, -7 = 3, -8 = 2, -9 = 1 .
A geometrical interpretation is shown in the adjacent figure. The negative circular direction is clockwise. Zero shows the starting marker. -3 is goes 3 markers in the negative direction. That is equivalent to going +7 in the positive direction. Also, -26 would go 26 markers in the negative direction which is equal to two complete rotations in the negative direction plus 6 markers, stopping at -6. But the marker at -6 is the same as the marker at +4. Therefore -26 = 4 (mod 10). For more discussion of finding non-negative remainders of negative integers in a mod system click here.
Absolute value is not defined for mod integers, because of their circular nature.
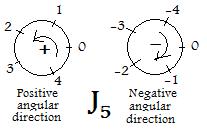 The additive inverses allow a method to solve some simple equations with mod integers. The pairs of additive inverses for J5 are: 0 and 0, 1 and 4, 2 and 3 as can be seen from a comparison of the adjacent figures.
The additive inverses allow a method to solve some simple equations with mod integers. The pairs of additive inverses for J5 are: 0 and 0, 1 and 4, 2 and 3 as can be seen from a comparison of the adjacent figures.
To solve the equation:
x + 4 = 2 (mod 5)
add the additive inverse of 4, namely 1, to both sides of the equation:
x + 4 + 1 = 2 + 1 (mod 5)
x + 0 = 3 (mod 5)
x = 3.
Check using x=3, 3 + 4 = 2 (mod 5).
For solving more simple equations involving the mod integers, click here.
Up to this point, use of division was made informally, namely in deciding factors of integers and remainders after denominators were divided into numerators. But in the mod integer systems Jn a more sisgnificant use of division may be made. Start with inverses. Recall [3.5a] (Additive inverses)
If the sum of two integers is zero (0) then each is called the additive inverse of the other.
The following is the (dual) definition for multiplication:
[3.12] (Multiplicative inverses*)
If the product of two numbers is unity (1) then each is called the multiplicative inverse of the other.
For commutative systems the multiplicative inverses are also called reciprocals.
One test for the multiplicative inverse of an integer u is to find a solution to ux = 1 where some integer replaces x.. The negative number -1 is its own multiplicative.inverse because the product (-1)(-1) = 1. Similarly, 1 is its own multiplicative inverse. Trivially, only 1 and -1 have multiplicative inverses in the system J of whole integers. The inverses of other integers involve fractions which are not equivalent to integers and are not in the system J. Zero times any number is never 1.
However, non-trivial multiplicative inverses exist in the mod integers (except in J2).
For example in J5 the equations
1x1=1, 2x3=1, 3x2=1, 4x4=1
show that 1,2,3,4 have multiplicative inverses (reciprocals) 1,3,2,4 (mod 5).
 To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
 The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
 By placing all the weights on one platform and no weights on the other platform the machine converts natural numbers (the weights themselves) into signed integers (as seen in the rectangular window on the scale). After locating a point O (the origin) the integers locate points indicated by vertical markers on the line as shown in the figure to the right. The weights themselves determine how far a marker is from the origin. The integer +4 is the weight 4 on the platform on the right (nothing on the left platform) and 4 is the disstance between the origin and the marker. Similarly -3 is associated with a marker on the left of O. The weight there is 3 (no weights on the right platform) and he distance between the marker and O is 3. Zero 0 and the origin O coincide.
By placing all the weights on one platform and no weights on the other platform the machine converts natural numbers (the weights themselves) into signed integers (as seen in the rectangular window on the scale). After locating a point O (the origin) the integers locate points indicated by vertical markers on the line as shown in the figure to the right. The weights themselves determine how far a marker is from the origin. The integer +4 is the weight 4 on the platform on the right (nothing on the left platform) and 4 is the disstance between the origin and the marker. Similarly -3 is associated with a marker on the left of O. The weight there is 3 (no weights on the right platform) and he distance between the marker and O is 3. Zero 0 and the origin O coincide.
 As a reminder of additive inverses, a person could write for J10 with its mod 10 system
As a reminder of additive inverses, a person could write for J10 with its mod 10 system The additive inverses allow a method to solve some simple equations with mod integers. The pairs of additive inverses for J5 are: 0 and 0, 1 and 4, 2 and 3 as can be seen from a comparison of the adjacent figures.
The additive inverses allow a method to solve some simple equations with mod integers. The pairs of additive inverses for J5 are: 0 and 0, 1 and 4, 2 and 3 as can be seen from a comparison of the adjacent figures.