Section 4 Mod Integers Jn
The "strange" systems discussed in this section are not part of the integer system, but are derived from it. The systems have some physical and geometrical applications, but also they provide exceptions to some of the common rules for integers and other common number systems to which most people are accustomed. To simplify discussions these systems are derived from the non-negative integers. But most of the discussions are also valid for all the integers. For those situations the non-negative adjective may be removed.
 In the previous chapter the finite sets of natural numbers were introduced. For example P12 = {1,2,3,4,5,6,7,8,9,10,11,12} provides the numbers on the face of a clock. But P12 is part of the collection of natural numbers which are represented geometrically as labeled markers lying on a straight line. In the listing for P12 there are no numbers that appear after the last number 12 nor before the first number 1.
In the previous chapter the finite sets of natural numbers were introduced. For example P12 = {1,2,3,4,5,6,7,8,9,10,11,12} provides the numbers on the face of a clock. But P12 is part of the collection of natural numbers which are represented geometrically as labeled markers lying on a straight line. In the listing for P12 there are no numbers that appear after the last number 12 nor before the first number 1.
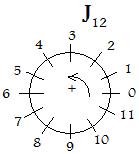 The finite collection J12 = {0,1,2,3,4,5,6,7,8,9,10,11} also has 12 numbers, but instead of the number 12, it has zero. Therefore it is part of the non-negative integers. But instead of lying on a straight line segment, J12 is best represented geometrically as labeled markers lying equally spaced on a circle. The numbers are arranged in a counterclockwise (+) circular direction (opposite to the forward motion of the hands of a clock). In this system noon and midnight are represented as zero.
The finite collection J12 = {0,1,2,3,4,5,6,7,8,9,10,11} also has 12 numbers, but instead of the number 12, it has zero. Therefore it is part of the non-negative integers. But instead of lying on a straight line segment, J12 is best represented geometrically as labeled markers lying equally spaced on a circle. The numbers are arranged in a counterclockwise (+) circular direction (opposite to the forward motion of the hands of a clock). In this system noon and midnight are represented as zero.
Markers on a circle provide a physical-geometrical method of addition, always done by counting markers in the + direction. In J12 this special addition is called mod 12 addition. To the sum 9 + 5, start with marker 9 and go 5 more markers in the + circular direction. The motion stops at the marker with the label 2. (9 o'clock plus 5 hours is equal to 2 o'clock.) It is customary to write 9 + 5 = 2 (mod 12).
A geometrical interpretation of this addition if the following. The marker for 9 is part way (more exactly 3/4 the way) around the circle in the + direction. Going 5 more markers continues past 0 and continues on for 2 more markers. Thus the motion makes a complete revolution around the circle plus 2 more markers.
The geometrical interpretation ignores the number of revolutions and considers the number of markers past 0. This suggests the division algorithm, which is the algebraic method for computing the sum mod 12. Perform ordinary addition (as done in the system of non-negative integers) to get the sum. Then divide 12 into the sum and look at the remainder:
9 + 5 = 14, 14 = 12(1) + 2 imply 9 + 5 (mod 12) = 2
The 1 is the number of revolutions and the 2 is the number of markers past zero.
The above example is a particular case of the system of integers Jn mod n. The systems
J2, J10, J24, J360
are other examples, where n = 2,10,24 and 360. (In the mod n system, n is a natural number greater than 1.) For each n, there is a special addition (mod n).
For example, find 9 + 8 (mod 10). 9 + 8 = 17, 17 = 10(1) + 7. Therefore 9 + 8 = 7 (mod 10).
mod addition can be easily extended to non-negative integers. To find 356 + 879 (mod 10),
356 + 879 = 1235, 1235 = 10(123) + 5, imply 356 + 879 (mod 10) = 5
But for mod 10 addition, only the last digit of any non-negative integer is important. Instead of adding 356 and 879, add 6 + 9. 6 + 9 (mod)10 = 15(mod 10) = 5. Therefore the "mod" operator may be applied to individual numbers. (Support for this statement is given in the volume on groups in the section on homomorphisms).
The problem may be phrased, reduce 1234 to a number in J7. Apply the division algorithm.
1234 = 7(176) + 2. Therefore 1234 = 2 (mod 7).
This problem is equivalent to finding the sum 1234 + 0 (mod 7). It is also equivalent to asking: find the number in
J7 such that 1234 = x (mod 7).
Multiplication of numbers in Jn mod n in a way similar to addition of the numbers. To find 7x9 (mod 6):
7x9 = 63, 63 = 3 (mod 6).
There are infinitely many non-negative integers, but only a finite number n of numbers in Jn. It is certain that many non-negative integers all reduce to the same number in Jn. For example,
2,9,16,23,30,37,44,51,...
all reduce to 2 (mod 7). Start with 2 and (using ordinary addition) add 7 repeatedly. Similarly, all the non-negative integers that reduce to 5 in J7 are
5,12,19,26,33,40,47,54,...
Another question: do the integers 4321 and 4907 reduce to the same number in J8 ? The answer is yes, because
4321 = 8(540) + 3 and 4907 = 8(613) + 3
That is 4321 = 3 (mod 8) and 4907 = 3 (mod 8).
Therefore 4321 = 4907 (mod 8).
The following fact shows a much quicker way to see if two integers are equivalent mod n:
[4.1] (Equivalence mod n) Two integers are equivalent mod n iff their difference is completely divisible by n.
u =v (mod n) if and only if u - v is divisible by n.
This statement is often used as the definition of two integers being equivalent mod n. Click here for the proof.
The integers 105 and 25 are equivalent mod 10 because 105 - 25 = 80 is completely divisible by 10. Subtraction the other way produces the difference -80, which is also divisible by 10.
It is possible to expand these collections by repeated subtractions. By subtracting 7 from 2 and subtracting 7 from 5 repeatedly, the following collections of integers are obtained:
Now subtract 7 from 2 repeatedly and attach the results to the above to get:
 In the previous chapter the finite sets of natural numbers were introduced. For example P12 = {1,2,3,4,5,6,7,8,9,10,11,12} provides the numbers on the face of a clock. But P12 is part of the collection of natural numbers which are represented geometrically as labeled markers lying on a straight line. In the listing for P12 there are no numbers that appear after the last number 12 nor before the first number 1.
In the previous chapter the finite sets of natural numbers were introduced. For example P12 = {1,2,3,4,5,6,7,8,9,10,11,12} provides the numbers on the face of a clock. But P12 is part of the collection of natural numbers which are represented geometrically as labeled markers lying on a straight line. In the listing for P12 there are no numbers that appear after the last number 12 nor before the first number 1.
 The finite collection J12 = {0,1,2,3,4,5,6,7,8,9,10,11} also has 12 numbers, but instead of the number 12, it has zero. Therefore it is part of the non-negative integers. But instead of lying on a straight line segment, J12 is best represented geometrically as labeled markers lying equally spaced on a circle. The numbers are arranged in a counterclockwise (+) circular direction (opposite to the forward motion of the hands of a clock). In this system noon and midnight are represented as zero.
The finite collection J12 = {0,1,2,3,4,5,6,7,8,9,10,11} also has 12 numbers, but instead of the number 12, it has zero. Therefore it is part of the non-negative integers. But instead of lying on a straight line segment, J12 is best represented geometrically as labeled markers lying equally spaced on a circle. The numbers are arranged in a counterclockwise (+) circular direction (opposite to the forward motion of the hands of a clock). In this system noon and midnight are represented as zero.