Go to other chapters or to other branches of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer programs

Chapter 6
Linear Transformations

Subsets of geometric points can form recognizable objects: lines, circles, squares, cones,... . Some of these objects are more fundamental to discussions here: points, lines, planes, entire 3 dimensional space. They may be called basic affine objects. They have dimensions 0,1,2, and 3 respectively. They are fundamental parts of the subjects of plane and solid geometry in which figures and solids are located. If they contain special points called origins, then they are basic linear objects. The term "basic" will often be omitted in these discussions

Section 1:   Matrices as Functions

In previous discussions arrays were written horizontally. It is possible to consider horizontal ordered pairs (x,y) as 1x2 matrices and horizontal triples (x,y,z) as 1x3 matrices. As such these "thin" matrices have 2x1 and 3x1 "thin" transposes:
These may be called vertical arrays. Sometimes in "fatter" matrices it is useful to consider its rows as a collection of horizontal arrays and its columns as a collection of vertical arrays.
It is possible to convert any horizontal array into a vertical array by transposition. In the following discussions, (x,y)' will denote the vertical transpose of the horizontal array (x,y). Similarly for (x,y,z)' .
Each point will have two "attached" arrays, the usual horizontal array and its vertical transpose. Therefore both (1,2) and (1,2)' locate the same point in the plane. Similarly, (1,2,3) and (1,2,3)' locate the same point in space.

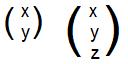
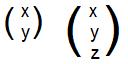
Consider the 3x2 matrix M:

According to the row*column rule of matrix multiplication:
In horizontal notation this can be written M(6,7)' = (33,16,-17)' . Similarly, the following equations are true: M(3,-1)' = (9,13,-11)', M(-2,5)' = (11,-20,-3). Using the arbitrary point (x,y)' in the plane, a formula is obtained for finding the image of the arbitrary point (x,y)'. The image point is (2x + 3y, 5x -2y, -4x + y)'. Because
M(x,y)' = (2x + 3y, 5x -2y, -4x + y)'
it may be said that M carries the point (x,y)' onto the point (2x + 3y, 5x -2y, -4x + y)' . In particular, M carries (6,7)' onto (33,16,-17)'. This sounds like M is acting as a function, carrying points (vertical ordered pairs) in a plane onto points (vertical ordered triples) in space.
However, functions are written in horizontal notation, and therefore involve horizontal arrays. The function F defined by
F(x,y) = (2x + 3y, 5x -2y, -4x + y)
also carries the points in the plane onto the same points in space as M does: F(6,7) = (33,16,-17), F(3,-1) = (9,13,-11), F(-2,5) = (11,-20,-3). Acting as carriers of points onto points, the matrix M "acts on" vertical arrays and produces vertical arrays, while the function F "acts on" the corresponding horizontal arrays and produces horizontal arrays.

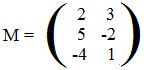
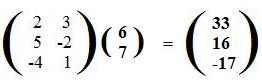
[1.1] (Matrices and Corresponding Functions ) A function F corresponds to a matrix M   and   a matrix M corresponds to a function F if and only if M and F carry the same points in some linear object onto the same points in some linear object, M doing it by operating on the vertical array labels, and F doing it by operating on the horizontal array labels attached to points.

When a matrix multiplies a vertical array (x,y)' or (x,y,z)' the result is a vertical array whose coordinates are always linear expressions. A linear expression in x and y is an expression of the form   αx + βy   A linear expression in x, y and z is an expression of the form   αx + βy + γz.   The symbols   α, β and γ   are any real numbers, and are called coefficients.

For example,   2x + 3y,   5x - 2y   -4x + y   are linear expressions in x and y. Also   5x + 6y - 7z   is a linear expression in x,y and z. The numbers,   2,3, 5,-2, -4,1,   5,6,-7   are coefficients. (Linear expressions are similar to linear combinations, but expressions involve only numbers and combinations involve vectors and numbers.)

It is important to notice that in a linear expression, every term has a single x, or y, or z in it. For this reason, linear expressions are said to be homogeneous. An expression like   5x + y + 4   is not a linear expression because the term   4   does not contain one of the three letters. Also   x2 + 4y   is not a linear expression because   x2   is really two x's. Obviously,   sin x + 7y   cannot be a linear expression.

The multiplication of a matrix M and a random vertical array (x,y)' or (x,y,z)' produces a vertical array whose coordinates are linear expressions in x,y or x,y,z. These linear expressions can be used in the definition of the corresponding function F. The coefficients of these linear expressions also determine matrix M. The coefficients   2,3, 5,-2,  -4,1   of the linear expressions   2x + 3y,   5x - 2y   -4x + y   determine the respective rows of the matrix M. The linear expressions themselves form the definition of the corresponding function F by means of the equation F(x,y) = (2x + 3y, 5x - 2y, -4x + y).

[1.2] Let F be a function from the plane into a linear object. Then F corresponds to a matrix M that does the same thing if and only if F carries the arbitrary point (x,y) onto a point whose coordinates equal to the linear expressions obtained by multiplying M by (x,y)' .   Similarly, let F be a function from space into a linear object. Then F corresponds to a matrix M that does the same thing if and only if F carries the arbitrary point (x,y,z) onto a point whose coordinates equal to the linear expressions obtained by multiplying M by (x,y,z)' .

If the x,y and z if any are replaced by zeros then the evaluations of linear expressions in x,y and in x,y,z are zeros. Therefore,

[1.3] If a function from a linear object into a linear object corresponds to a matrix then that function must carry the origin onto the origin.


Section 2:   Linear Transformations

Since linear objects have origins, position vectors exist. In this section the "carrying power" of functions is extended from horizontal and vertical array labels to carrying position vectors. Let F be a function from a linear object into a linear object, and suppose that F carries the origin onto the origin.. For any points P,Q,R in the first linear object, F(P), F(Q), F(R) are image points in the second linear object. Let P', Q', R' denote these images. By supposition F[O] = O. Therefore, F carries the position vectors OP, OQ, OR onto position vectors OP', OQ', OR'. Hence, F(p) = p', F(q) = q', F(r) = r'.

If F corresponds to a matrix, then by [1.3] F carries the origin onto the origin, and hence it carries position vectors onto position vectors.

For a motivation using methods from high school geometry for the following definition click here.

[2.1] (Linear transformations) A function F from a linear object to a linear object is a linear transformation if and only if it satisfies the following two conditions:
  (a) F(p + q) = F(p) + F(q);     (homomorphism)
  (b) F(λp) = λF(p)     (homogeneous)
where p and q are any (position) vectors in the first linear object and λ is any real number.

Remark: These conditions imply that a linear transformation carries the zero vector onto the zero vector (and therefore the origin onto the origin). Simply let λ = 0 in condition (b).

Example:
Consider the function F from any linear object onto itself, defined by F(p) = 2p, for every point P in the first linear object.. Then F(q) = 2q, F(r) = 2r for position vectors q,r.... Intuitively speaking, F stretches any position vector to another vector pointing in the same direction but twice the length. F satisfies both conditions (a) and (b) of [2.1]:
  (a) F(p + q) = 2(p + q) = 2p + 2q = F(p) + F(q).
  (b) F(λp) = 2(λp) = λ(2p) = λF(p).

The following is a generalization of the defintion [2.1] of a linear transformation.

[2.2] Every linear transformation carries any linear combination of position vectors onto a linear combination of position vectors with the same coefficients.
Notation: If F is a linear transformation then F(λp + σq + ... + ωr) = λF(p) + σF(q) + ... + ωF(r).


In a linear object position vectors locate points, and to those points are "attached" linear arrays. Therefore, linear arrays can be represented by position vectors. If a position vector p in a plane locates a point P(x,y), then p = (x,y). Similarly, if p in space locates point P(x,y,z) then p = (x,y,z). As a result,definition [2.1] may be stated for linear arrays by replacing p and q by their equals (x1,y1) and (x2,y2):   F(p) = F(x1,y1), and F(q) = F(x2,y2). Similarly if F is from space: F(p) = F(x1,y1,z1), and F(q) = F(x2,y2,z2).   (Here the two F's denote different functions because they involve different linear objects, namely plane and space.)

Example: The function F defined by F(x,y) = (x + y, x - y) is a linear transformation from a plane onto itself. It carries point (1,1) onto point (2,0), point (5,3) onto (8,2). Click here to see the proof that it satisfies both conditions

(a)      F((x1,y1) + (x2,y2)) = F(x1,y1) + F(x2,y2)
and
(b)      F(λ(x,y)) = λF(x,y)                                  

The following functions F,G,H are also linear transformations:

F(x,y,z) = (2x + 3y + 4z, 4x - y - 3z, x +6y + z),      G(x,y,z) = (4x - y + z, 2x + 7y +5z),      H(x,y) = (x + y, x - y, 3x + 2y)
From the lengths of the arrays involved, it is easy to see that
F carries space into space,         G carries space into a plane;         H carries a plane into space

[2.3] A function from a plane into a linear object is a linear transformation if and only if carries an arbitrary point (x,y) onto a point whose coordinates are linear expressions of x and y. A function from space is a linear transformation if and only if it carries an arbitrary point (x,y,z) onto a point whose coordinates are linear expressions of x,y and z.



The pair of special unit arrays in a plane   (1,0) = i and (0,1) = j   as well as the triple of special unit arrays in space   (1,0,0) = i, (0,1,0) = j and (0,0,1) = k   play special roles with linear transformations.

Example: suppose F(1,0) = (4,5) and F(0,1) = (6,7). Onto what point does F carry the arbitrary point (x,y)? Notice that array (x,y) = x(1,0) + y(0,1). Then F(x,y) = xF(1,0) + yF(0,1) = x(4,5) + y(6,7) = (4x + 6y, 5x + 7y). Therefore, F carries the arbitrary point (x,y) onto the point (4x + 6y, 5x + 7y). This fact completely defines and determines F.

[2.4a] (Linear transformation from the plane is determined by images of two special points) From the identity

F(x,y) = xF(1,0) + yF(0,1)
a linear transformation F from the plane into a linear object is completely determined by the two image points F(1,0) and F(0,1).

[2.4b] (Linear transformation from space is determined by images of three special points) From the identity

F(x,y,z) = xF(1,0,0) + yF(0,1,0) + zF(0,0,1)
a linear transformation F from space into a linear object is completely determined by the three image points F(1,0,0), F(0,1,0), and F(0,0,1).

The expression xF(1,0) + yF(0,1) is actually an array whose coordinates are linear expressions in x and y. If F(1,0) = (α1, β1) and F(0,1) = (α2, β2) then

(#)        xF(1,0) + yF(0,1) = (α1x + β1y, α2x + β2y)
In a similar way, it is easy to show that if F(1,0,0) = (α1, β1, γ1), F(0,1,0) = (α2, β2, γ2) and F(0,0,1) = (α3, β3, γ3) then
(##)        xF(1,0,0) + yF(0,1,0) + zF(0,0,1) = (α1x + β1y + γz1, α2x + β2y + γz2, α3x + β3y + γ3z)
By eliminating or adding coordinates itis possible to produce further arguments supporting theorem [2.3].

The coefficients of the linear expressions in (#) and (##) can be collected into matrices M2 and M3:

[2.5a] (Linear transformations from a plane into some linear object) If F is any linear transformation from a plane into some linear object then F(x,y)' = M(x,y)' where M is the matrix

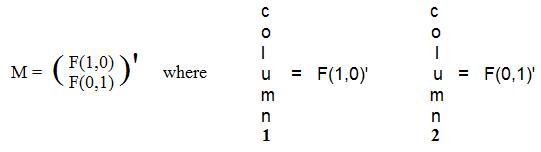
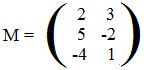
Example. In the discussion just before [1.2] F was defined by F(x,y) = (2x+3y, 5x-2y, -4x+y). Then F(1,0) = (2, 5, -4) and F(0,1) = (3, -2, 1). These become the column arrays (2, 5, -4)' and (3, -2, 1)' in the corresponding matrix M:

[2.5b] (Linear transformations from space into some linear object) If F is any linear transformation from space into some linear object then F(x,y,z)' = M(x,y,z)' where M is the matrix

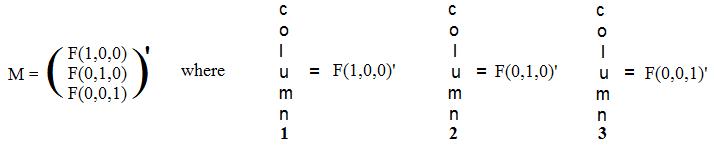
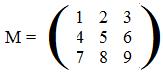
Example. In the discussion before [1.2] F was defined by F(x,y,z) = (x+2y+3z, 4x+5y+6z, 7x+8y+9z) and the matrix M that corresponds to F is:
Then F(1,0,0) = (1, 4, 7), F(0,1,0) = (2, 5, 8), F(0,0,1) = (3, 6, 9) from which the column arrays (1, 4, 7)', (2, 5, 8)', (3, 6, 9)' in matrix M are formed.

Recall that if a function F carries a point P onto a point Q, and a function G carries point Q onto a point R, then the composite GF carries P onto R.

[2.6] (Composition of linear transformations) The composite of two linear transformations is a linear transformation.
Notation: if F and G are linear transformations, then GF is a linear transformation.

F carries a position vector p + q onto a position vector F(p + q). Then G carries F(p + q) onto GF(p + q). But GF(p + q) = G(F(p) + F(q)) = GF(p) + GF(p + q). Also GF(λp) = G(λF(p)) = λGF(b>p); Therefore GF is a linear transformation. As was mentioned earlier, linear transformations and their corresponding matrices behave the same way, except for notation. Therefore, the following statement comes as no surprise.

[2.7] (Composition and matrix product) The matrix that corresponds to the composite of two linear transformations is equal to the product in the same order of the matrices that correspond to the individual linear transformations.
Notation: If M is the matrix that corresponds to linear transformation F, and N is the matrix that corresponds to linear transformation G, then the (matrix) product MN of the two matrices is the matrix that corresponds to the composite GF of the two transformations.

[2.1b] (Linear transformations and matrices) A function from a linear object to a linear object is a linear transformation if and only if there exists a corresponding matrix for the function.