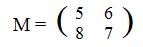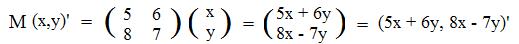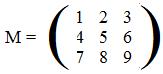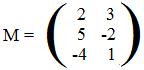Return to Chapter 6
Additional Material for Chapter 6
Chain of Equalities for F(x,y) = (2x,3y) to be a Linear Transformation
F(p + q) = F((x1,y1) + (x2,y2)) = F(x1+x2, y1+y2) =
(2(x1+x2), 3(y1+y2)) =
(2x1,3y1) + (2x2,3y2) =
F(x1, y1) + F(x2, y2) = F(p) + F(q)
Geometric approach to linear transformations
Since these linear objects are sets, there exist functions that carry all the points from a linear object onto a linear object. These functions will be given some further conditions to become acceptable functions. For example, a function may carry all the points of a line onto a line. It is possible to find a function that carries an entire plane onto a single line. A function that carries a line onto a semi-circle would not be considered acceptable since a semi-circle is not one of the four linear objects. Another condition on acceptable functions is that the origin is carried by them onto the origin. A function that carries an entire linear object onto a single point (it must be an origin) is called trivial or constant. Such functions are acceptable, but not very interesting.
One of the geometric figures that receives much attention in these discussions is the parallelogram. Only functions that preserve the form of a parallelogram will be acceptable. This means that if points O,P,R,Q are vertices of a parallelogram, then images O,F(P),F(R),F(Q) must also be vertices of a parallelogram. (See adjacent Fig1.) A slight problem occurs if F carries all of the points in the first linear object onto points of some line. Then the four images are points of a "collapsed parallelogram".
(See adjacent Fig2.). Click here to see a discussion of collapsed parallelograms.
The opposite sides of a parallelogram are parallel. This forces acceptable non-trivial functions to carry parallel lines onto parallel lines. (Assume that any line is parallel to itself.) Such functions are said to "preserve parallelism." There are functions in a higher geometry, called projective geometry, that carry lines onto lines but do not preserve parallelism.
There is another condition that "acceptable functions" must satisfy. Given any two parallel line segments. They may or not be congruent. However, a quotient of their lengths forms a ratio. An acceptable function will carry these parallel segments onto parallel segments preserving the ratio of their lengths. Therefore, if A and B are the end points of the first segment, and C and D are the end points of the second segment, then F(A) and F(B) are the end points of the image of the first segment, and F(C) and F(D) are the end points of the image of the second segment. Then if λ = length AB/lengthCD then also λ = length F(A) F(B)/length F(C) F(D) if F(C) and F(D) are distinct.
It should be emphasized that an acceptable function need not preserve lengths, only the ratio of lengths. It can carry a trapezoid onto a much larger or much smaller trapezoid, but the ratio of lengths of the parallel sides of each trapezoid must be the same. The ratio condition exists only if the segments are parallel. Parallel segments become congruent if the ratio of their lengths = 1.
[2.1] (Acceptable functions) A function is acceptable if it satisfies all of the following conditions:
(a) It carries all of the points of some linear object onto a linear object;
(b) It carries the orgin of the first linear object onto the origin of the second linear object;
(c) If two line segments are parallel, then it carries them onto parallel line segments, providing they are not points. Furthermore, the ratio of the lengths of the segments in the first linear object equals the ratio of the lengths of the segments in the second linear object.
(d) It carries the four vertices of a parallelogram in the first linear object onto the four vertices of a parallelogram in the second linear object.
The acceptable functions belong to "linear geometry". If condition (b) is removed, then the functions only belong to "affine geometry."
Some of these conditions are redundant. It is possible to prove (d) from (c).
The use of position vectors makes the discussion shorter and, hopefully, more understandable. Since linear objects contain an origin O, position vectors exist and any point may be located by a position vector: p = OP locates point P in some linear object. Let F be a function from that linear object onto a linear object. Then F carries point P onto some point F(P) in the second linear object and therefore F(p) = F(OP) = F(O)F(P) = OF(P) is a position vector from O to point F(P) and locates point F(P) in the second linear object. It will be convenient in discussions to switch between points and their position vectors that locate the points. Therefore, F carries points onto points as well as their position vectors onto position vectors.
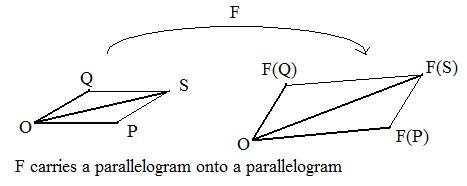 The sum of two position vectors p and q can be done in geometry using a parallelogram. The points Q, O, P are three adjacent vertices of the parallelogram. The fourth point S is located by the position vector OS which is a diagonal of the parallelogram. If F is an acceptable function then F carries the origin onto the origin and parallelograms onto parallelograms. Therefore, points F(Q),O,F(P) are three of the vertices of a parallelogram. The fourth point is is located by a position vector obtained by addition of vectors F(p) and F(q). But the acceptable function carries parallelogram onto parallelogram and therefore carries point S onto this fourth point. Therefore,
The sum of two position vectors p and q can be done in geometry using a parallelogram. The points Q, O, P are three adjacent vertices of the parallelogram. The fourth point S is located by the position vector OS which is a diagonal of the parallelogram. If F is an acceptable function then F carries the origin onto the origin and parallelograms onto parallelograms. Therefore, points F(Q),O,F(P) are three of the vertices of a parallelogram. The fourth point is is located by a position vector obtained by addition of vectors F(p) and F(q). But the acceptable function carries parallelogram onto parallelogram and therefore carries point S onto this fourth point. Therefore,
F(p) + F(q) = OF(S) = F(OS) = F(p + q)
for any position vectors p and q in the first linear object
Therefore,
(*) F(p + q) = F(p) + F(q)
This makes F an additive homomorphism. All additive homorphisms carry 0 onto 0. To show this, since 0 = 0 + 0, F(0) = F(0 + 0) = F(0) + F(0). Then subtract F(0) from the equation just found, F(0) = F(0) + F(0) to get 0 = F(0).
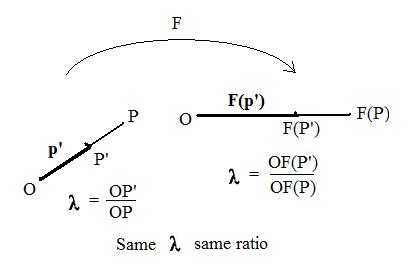 Let P' be any point on the line through distinct points O and P. Suppose O is not between P' and P as shown in the adjacent figure. This makes the ratio λ = OP'/OP non-negative. An acceptable function F carries these collinear points onto collinear points O, F(P') and F(P). Because F preserves ratios of lengths of line segments, λ = OF(P')/OF(P). Therefore for both figures,
Let P' be any point on the line through distinct points O and P. Suppose O is not between P' and P as shown in the adjacent figure. This makes the ratio λ = OP'/OP non-negative. An acceptable function F carries these collinear points onto collinear points O, F(P') and F(P). Because F preserves ratios of lengths of line segments, λ = OF(P')/OF(P). Therefore for both figures,
OP' = λOP and OF(P') = λOF(P)
In the language of position vectors this translates into
p' = λp and F(p') = λF(p)
Replace p' in this last equation by λp to get
(*) Fλp) = λF(p)
But the discussion has supported this equality only for λ>0. (It is trivially true for λ=0.) Some simple manipulations will show that the equation is true for λ<0 without direct geometric support.
Since F is a homomorphism,
F(λp + (-λ)p) = F(λp) + F((-λ)p)
Therefore,
0 = F(0) = F(λp) + F((-λ)p)
This means that
F(λp) = - F((-λ)p)
But - λ >0 , so from the argument above, F((-λ)p) = (-λ)F(p). Therefore,
F(λp) = -(-λ)F(p)
or
(**) F(λp) = λF(p)
Equations (*) and (**) become necessary conditions that a function F be a linear transformation.
Linear Expressions Relate Matrices and Corresponding Functions
It is simple to find values for the linear expressions
(*) 5x + 6y and 8x - 7y
if numerical values are given to x and y. If x and y are given values 3 and 4 respectively, then the expressions become
5(3) + 6(4) = 39 and 8(3) - 7(4) = - 4
By giving other values to x and y simultaneously, the two expressions have numerical values. Form the horizontal arrays (3,4)'and (39,-4) . To the first array the linear expressions associate the second array. This action can be written
(3,4) --> (39,-4)
The expressions can also be applied to vertical arrays:
(3,4)' --> (39,-4)
The reader can easily verify:
(1,-1)' --> (-1,15)', (4,1)' --> (26,25)', (α,β)' --> (5α + 6β, 8α - 7β)'
Consider these arrays as locating points in a plane. For each point (x,y)' in the plane the expressions assign a unique point (5x+6y,8x-7y)'. But this action satisfies the definition of a function F, carrying points in a plane onto points in the same plane:
(**) F(x,y) = (5x+6y,8x-7y)
Here,
F(3,4) = (39,-4), F(1,-1) = (-1,15), F(4,1) = (26,25)
It is convenient to use the same function F for vertical arrays:
F(3,4)' = (39,-4)', F(1,-1)' = (-1,15)', F(4,1)' = (26,25)'
Using the coefficients of the linear expressions (*), form a 2x2 matrix:
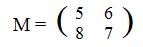 Thinking of M (x,y)' as a matrix product of a 2x2 and a 2x1 matrices:
Thinking of M (x,y)' as a matrix product of a 2x2 and a 2x1 matrices:
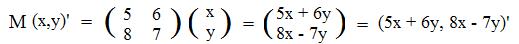 Compare this equation involving matrices with the definition (**) of function F, intuitively speaking, M and F do the same thing to points in the plane. More exactly, M and F perform the same action on the coordinates of every point in the plane. The only difference is that by notation F involes horizontal arrays, but M involves vertical arrays.
Compare this equation involving matrices with the definition (**) of function F, intuitively speaking, M and F do the same thing to points in the plane. More exactly, M and F perform the same action on the coordinates of every point in the plane. The only difference is that by notation F involes horizontal arrays, but M involves vertical arrays.
There is a similar discussion for 3x3 matrices and points in space. Given the linear expressions,
x + 2y + 3z, 4x + 5y + 6z, 7x + 8y + 9z
the function F can be formed: F(x,y,z) = (x+2y+3z, 4x+5y+6z, 7x+8y+9z) and the matrix M that corresponds to F is:
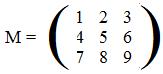 The reader can verify that the product M(x,y,z)' = (x+2y+3z, 4x+5y+6z, 7x+8y+9z)'.
The reader can verify that the product M(x,y,z)' = (x+2y+3z, 4x+5y+6z, 7x+8y+9z)'.
The linear expressions
2x + 3y 5x - 2y -4x + y
receive values for x and y and return values for the three expressions. Therefore, they carry points from a plane into space:
(x,y)' --> (2x+3y, 5x-2y, -4x+y)'
The function for this action is F defined by F(x,y) = (2x+3y, 5x-2y, -4x+y). The matrix is
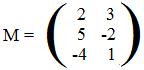 For example, Let M act on point (6,7)' and let F act on the same point (6,7):
M(6,7)' = (2(6)+3(7), 5(6)-2(7), -4(6)+1(7))' = (33, 14, -17)'
For example, Let M act on point (6,7)' and let F act on the same point (6,7):
M(6,7)' = (2(6)+3(7), 5(6)-2(7), -4(6)+1(7))' = (33, 14, -17)'
F(6,7) = (33, 14, -17).
By the matrix product a non-square matrix "changes" a column array of some length into a column array of a different length. The corresponding function carries an array of some length onto an array of a different length. Intuitively speaking, they both carry points in some dimension onto points in another dimension.
 The sum of two position vectors p and q can be done in geometry using a parallelogram. The points Q, O, P are three adjacent vertices of the parallelogram. The fourth point S is located by the position vector OS which is a diagonal of the parallelogram. If F is an acceptable function then F carries the origin onto the origin and parallelograms onto parallelograms. Therefore, points F(Q),O,F(P) are three of the vertices of a parallelogram. The fourth point is is located by a position vector obtained by addition of vectors F(p) and F(q). But the acceptable function carries parallelogram onto parallelogram and therefore carries point S onto this fourth point. Therefore,
The sum of two position vectors p and q can be done in geometry using a parallelogram. The points Q, O, P are three adjacent vertices of the parallelogram. The fourth point S is located by the position vector OS which is a diagonal of the parallelogram. If F is an acceptable function then F carries the origin onto the origin and parallelograms onto parallelograms. Therefore, points F(Q),O,F(P) are three of the vertices of a parallelogram. The fourth point is is located by a position vector obtained by addition of vectors F(p) and F(q). But the acceptable function carries parallelogram onto parallelogram and therefore carries point S onto this fourth point. Therefore,
 Let P' be any point on the line through distinct points O and P. Suppose O is not between P' and P as shown in the adjacent figure. This makes the ratio λ = OP'/OP non-negative. An acceptable function F carries these collinear points onto collinear points O, F(P') and F(P). Because F preserves ratios of lengths of line segments, λ = OF(P')/OF(P). Therefore for both figures,
Let P' be any point on the line through distinct points O and P. Suppose O is not between P' and P as shown in the adjacent figure. This makes the ratio λ = OP'/OP non-negative. An acceptable function F carries these collinear points onto collinear points O, F(P') and F(P). Because F preserves ratios of lengths of line segments, λ = OF(P')/OF(P). Therefore for both figures,