Return to main page

Volume E   Chapter 3
Additional Material

[1.1] Linear transformation on space

Let α, β and γ represent any real numbers. The expression   αx + βy + γz   is called a linear expression in x,y and z
A linear transformation L on coordinate spsace has its formula defined by linear expressions in x,y and z:
L(x,y,z) = (α1x + β1y + γ1z,    α2x + β2y + γ2z,    α3x + β3y + γ3z)
Example of a linear transformation on space:
   L(x,y,z) = (x + y + z, 3x + 4y -2z, -x +y)


Proof of [1.4]

[1.4] (Properties of any linear transformation on the coordinate plane) Let L be any linear transformation on the coordinate plane, let (x,y), (x1, y1), (x2, y2) be any points in that plane and let λ be any real number. Then L satisfies the following two conditions:
  (a) L( (x1, y1) +(x2, y2) ) = L(x1, y1) + L(x2, y2).
  (b) L( λ(x,y) ) = λL(x,y).

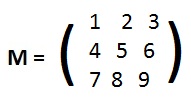
In words, L carries the sum of two points onto the sum of their images. L carries the product of a real number and a point onto the product of that real number and the image of the point.

Recall that arrays may be added and multiplied by a real number λ:
   (a) (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2);
  (b) λ(x,y) = (λx, λy)

Basic to the proof is the 2x2 matrix M associated with L. In a prevfious chapter there was a discussion about a distributive law for matrices.
L(x1, y1) + L(x2, y2) = (x1, y1)M + L(x2, y2)M = (x1 + x2, y1 + y2)M = L( (x1 + x2, y1 + y2) ).

L( λ(x,y) ) = L(λx,λy) = (λx, λy)M = λ(x,y)M = λL(x,y).


Example of a linear transformation very different from those on the coordinate plane or space

[1.5] A function L on a vector space is a linear transformation if and only if it has the following two properties, for all elements u and v in the vector space, and any real number λ:
   (a) L(u + v) = L(u) + L(v);
   (b) L(λv) = λL(v)

Consider the collection of all polynomials in x with real numbers as coefficients. The collection has all the properties of a vector space, including addition of polynomials and products with real numbers. The derivative operator d/dx is a function that carries each polynomial onto another polynomial (the derivative). For example,   d/dx (x2 + 4x +5) = 2x + 4.

Let p(x) and q(x) represent any polynomials in x with real number coefficients. By the rules of differentiation:
   (a) d/dx ( p(x) + q(x) ) = d/dx p(x) + d/dx q(x).
   (b) d/dx λp(x) = λ d/dx p(x).

Here   u = p(x),   v = q(x)     in (a),
v = p(x)     in (b) and
L = d/dx.



Geometric interpretations of the statement [1.6]

[1.5] (Defining properties of a linear transformation) A function L on a vector space is a linear transformation if and only if it has the following two properties, for all elements p and q in the vector space, and any real number λ:
   (a) L(p + q) = L(p) + L(q);
   (b) L(λp) = λL(p);
where u,v have been replaced by p,q.

Recall that vector addition is pictured as a parallelogram. P and Q are arbitrary points in the coordinate plane located by the position vectors p and q. Together with origin O they form three vertices of a parallelogram. To locate the fourth point R, construct and arc at P with radius |OQ| and an arc at Q with radius |OP|. Where the arcs intersect is point R. Therefore, for position vectors p,q,r

p + q = r

Do a very similar construction with the three points L(P),O, L(Q) with intersecting arcs intersecting at a point R'. Therefore,

L(p) + L(q) = r'
But by [1.5a]
L(p) + L(q) = L(p + q) = L(r)
Then L(r) and r' are equal to the same thing, namely L(p) + L(q), and are equal to each other.
This is part of support for a statement that linear transformations carry vertices of a parallelogram onto vertices of parallelogram. Later, a proof will remove the condition at the origin be one of the vertices.


Theorem [1.7] for coordinate space

[1.7] (Rows of the associated matrix) If L is any linear transformation on coordinate space then rows 1,2 and 3 of its associated matrix are the images L(1,0,0), L(0,1,0) and L(0,0,1) respectively.

Example: if   L(1,0,0) = (1,2,3),   L(0,1,0) = (4,5,6)   and   L(0,0,1) = (7,8,9)   then the matrix associated with L is




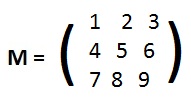
A linear transformation with a non-singular associated matrix carries distinct points onto distinct points

Let L be a linear transformation and M its non-singular associated matrix (see adjacent figure). Since
det M ≠ 0,
(*)      αδ − βγ ≠ 0.
Also since M is the associated matrix:
L(x,y) = (x,y)M = (αx + γy, βx + δy)
for any point (x,y).

Let   (x1, y1)   and   (x2, y2)   be any points. "Distinct points carried onto distinct points" can be translated as an implication

(x1, y1)   ≠   (x2, y2)      =>      L(x1, y1)   ≠   L(x2, y2)
The contrapositive of this implication is:
(**)      L(x1, y1)   =   L(x2, y2)     =>     (x1, y1)   =   (x2, y2)
The contrapositive will be proven using a chain of implications. In one of the chains let
(***)      x = x1 − x2   and   y = y1 − y2

Starting the chain with the hypotheses in (**) above:
L(x1, y1)    =    L(x2, y2)      =>
   (αx1 + γy1, βx1 + δy1) = (αx2 + γy2, βx2 + δy2)      =>
   (αx1 + γy1, βx1 + δy1) − (αx2 + γy2, βx2 + δy2)    =    (0,0)      =>
   (αx1 − αx2 + γy1 − γy2, βx1 − βx2 +δy1 − δy2)    =    (0,0)      =>
   (α(x1 − x2) + γ(y1 − y2), β(x1 − x2) + δ(y1 − y2))    =    (0,0)      =>
   (αx + γy, βx + δy)    =    (0,0)      =>

αx + γy = 0                  αx + γy = 0
βx + δy = 0                  βx + δy = 0      =>
[multiply left top equation by δ and left bottom equation by γ and subtract to get]         (αδ − βγ)x = 0.
multiply right top equation by β and right bottom equation by α and subtract to get]      (αδ − βγ)y = 0.

But (*) forces x=0 and y=0.
Then (***) forces x1= x2   and   y1= y2.
This proves (**).