Return to main page

Volume E   Chapter 2
Additional Material

Computing Entries in Product Matrix

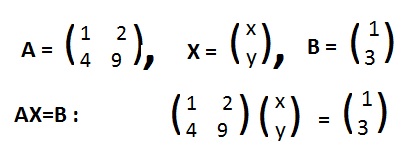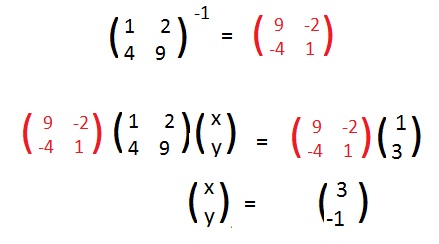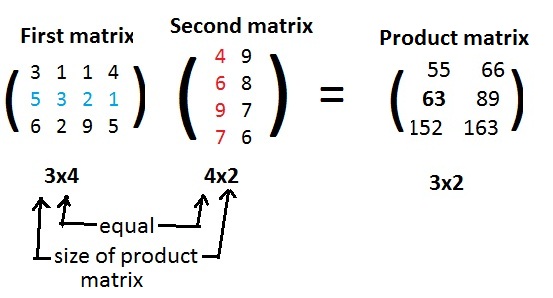
Row number in    Column number in     Dot product    (→)⋅(↓)             Location in Product Matrix
First Matrix     Second Matrix

       1             1     (3)(4) + (1)(6) + (1)(9) + (4)(7) = 55        55 in row 1, column 1
       1             2     (3)(9) + (1)(8) + (1)(7) + (4)(6) = 66        66 in row 1, column 2

       2             1    (5)(4) + (3)(6) + (2)(9) + (1)(7) = 63        63 in row 2, column 1
       2             2    (5)(9) + (3)(8) + (2)(7) + (1)(6) = 89        89 in row 2, column 2

       3             1    (6)(4) + (2)(6) + (9)(9)  + (5)(7) = 152     152 in row 3, column 1
       3             2    (6)(9) + (2)(8) + (9)(7)  + (5)(6) = 163     163 in row 3, column 2


Determinant value of a product of two 2x2 matrices is equal to the product of the determinant values of the two matrices

Let A and B be the two 2x2 matrices as shown. Then their product AB is computed and shown also.
The task is to prove
det (AB) = (det(A)(det(B))

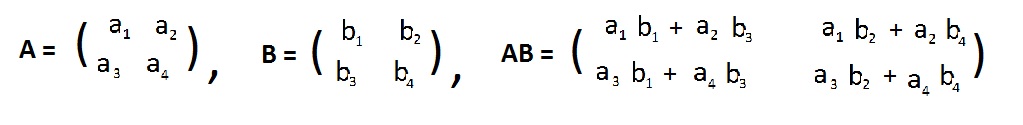
det(A) = a1a4 − a2a3
det(B) = b1b4 − b2b3
det(AB) = (a1b1 + a2b3) (a3b2 + a4b4) − (a1b2 + a2b4) (a3b1 + a4b3)
            = a1b1a3b2 + a1b1a4b4 + a2b3a3b2 + a2b3a4b4 − a1b2a3b1 − a1b2a4b3 − a2b4a3b1 − a2b4a4b3
            = a1b1a4b4 + a2b3a3b2 − a1b2a4b3 − a2b4a3b1
            = a1a4b1b4 − a1a4b2b3 − a2a3b1b4 + a2a3b2b3
            = (a1a4 − a2a3)(b1b4 − b2b3)
            = (det(A))(det(B)).



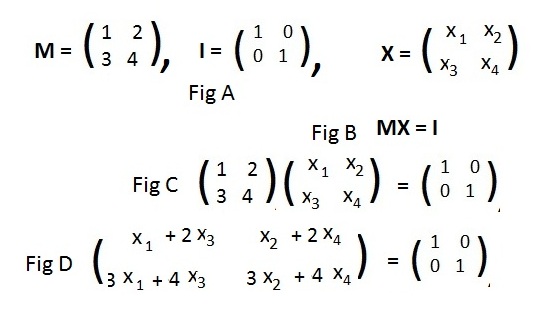Calculate the inverse of matrix M given below

The matrix M is given in Fig A to the right. The inverse matrix of M exists because  
det M = (1)(4() - (2)(3) = -2
shows that M is non-singular. In Fig A, I is the 2x2 identity matrix. Let X be the inverse of M. X has unknown entries   x1, x2, x3, x4. The task is to determine X by calculating values for the four entries.
Fig B says that X is the inverse of M.
Fig C replaces the names of the three matrices by the actual matrices.
Fig D shows the product matrix of the two matrices above it.

Matrix equality requires that all corresponding entries be equal. There are four equations in this case:

  x1 + 2x3 = 1       x2 + 2x4 = 0
3x1 + 4x3 = 0     3x2 + 4x4 = 1
Fig E is obtained using Cramer's rule.
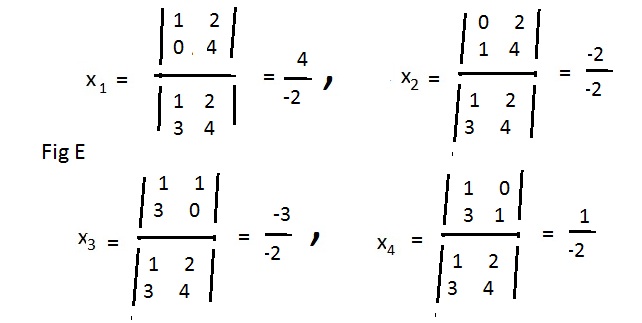Therefore the solutions are:
x1=-2,   x2=1,  x3=3/2,   x4=-1/2
The inverse matrix X is

Notice that the denominators of all four fractions are the same as   det M = -2.

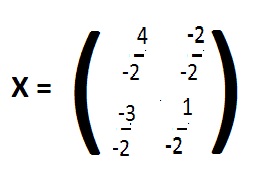
The computer calculates the adjoint
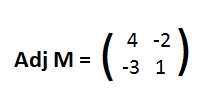
and then says to obtain the inverse divide the adjoint by Det M = -2. The results agree with X.

Intuitively speaking, the adjoint produces the numerators of the fractions, and the determinant value of the given matrix provides the denominators. For 3x3 a matrix, 9 linear equations must be solved to produce the adjoint. And for nxn matrices there are n2 equations that must be solved to compute the adjoint. The computer uses a different method to produce the adjoint, and does not solve any linear equations doing it. Nevertheless, the method involves much computation evaluating n2 determinants, which the computer does very fast and accurately.



Solving a system of linear equations using an inverse matrix

Given the linear equations
x + 2y = 1
4x + 9y = 3
The coefficient matrix is A and the equations become a matrix equation AX=B:
The inverse A-1 of the coefficient matrix A has already been calculated. Multiply both sides of AX=B by it to get a new matrix equation. Both sides reduce to equal column vectors.
From the equal column vectors, x=3, y=-1 which are solutions to the given linear equations above.