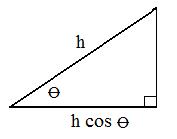Go to other chapters or to other books of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Volume D Chapter 4
Norm and Dot Product
Ideas and notations introduced in previous chapters continue in this chapter. There are two types of vectors, the drawn geometric position vectors, p,q,r,s in the plane or in 3-dimensional space, and the more abstract algebraic array (x,y) of size 2 or (x,y,z) of size 3 with coordinates x,y,z of real numbers. The arrays continue to serve dual roles, as labels attached to points, and as position vectors to those points. In particular, point P may have an attached array (1,2) , written P(1,2) or the array (1,2) may be said to locate point P, and then p = (1,2). This convention relates geometric position vectors with algebraic arrays, yet their ideas will often be developed separately. The geometric vectors are largely intuitive and pictorial and often provide understanding and motivation for various statements. The algebraic vectors, with their precisely defined characteristics, are used in proofs and arguments.
In this chapter additional and useful structure will be imposed on both the geometric and algebraic vector spaces of the previous chapters.. They will allow the measure of distance and angles, and much more. The characteristics of the two added structures will be listed in this chapter and summerized and listed in the next chapter for general vector spaces.
Section 1: Norm of a Vector
Distance is a familiar idea in high school geometry. The distance between two points A and B is measured along a straight line segment AB to produce a non-negative real number, denoted by |AB|. The segment joining A and B provides the shortest distance between A and B. Also the distance is the same if it is measured from A to B or from B to A along segment AB, because it is a scalar and not a vector. The length of a segment is the distance between its end points. The length of segment AB is denoted by |AB|. Distance or length is never negative, but it may be zero. This happens if and only if the end points A and B coincide, that is, a segment that is reduced to a single point.
 If the shortest distance between two points A and B is the length of the segment joining the points, then the distance is longer if a third point C is off of the segment AB and the measuring process between A and B is done by going through C, as shown in the adjoining figure. This fact can be demonstrated by an expression with a strict inequality symbol:
If the shortest distance between two points A and B is the length of the segment joining the points, then the distance is longer if a third point C is off of the segment AB and the measuring process between A and B is done by going through C, as shown in the adjoining figure. This fact can be demonstrated by an expression with a strict inequality symbol:
|AB| < |AC| + |CB|.
If A,B,C are vertices of a triangle, then there is a theorem from plane geometry that says the length of any side of a triangle is less than the sum of the lengths of the other two sides.
The equation involving lengths
|AB| = |AC| + |CB|
is true if and only if C is on segment AB. This is shown in the adjacent figure of a "collapsed" triangle.
For the genuine triangle and the collapsed triangle, the weak inequality
|AB| ≤ |AC| + |CB|
is true for both. It is called the "triangle inequality" for obvious reasons.
No genuine definition of length (or distance) has been given here. The above discussion reveals the defining characteristics of length applied to different segments. The idea of a length can be applied to a geometric vector by ignoring the direction of the vector and measuring the line segment. Then the length of the vector AB is the same as the length of the vector BA
|AB| = |BA|.
Both lengths are equal real numbers. Moreover, those real numbers are never negative, even though one vector may be the negative of the other (point in opposite directions).
[1.1] (Geometric concept of a norm)
(a)The norm of a (geometric) vector is length of the segment joining the tail point and the head point.
Notation: |AB| = |AB| (the length of segment AB).
In the case of a position vector, its norm is equal to the length of the segment joining the origin to the point located by the position vector.
So if position vector p locates point P then |p| = |OP|,
which is also the distance beetween the origin O and the point P.
In these discussions the same symbol | | is used for both norms of vectors and absolute values of numbers. If a vector is between the vertical bars, then it is a norm. But if a real number is between the bars, it is an absolute value. However, the distinction is not made in these discussions because absolute value has all the characteristics of a norm: a vector drawn from 0 to a real number is a position vector that locates that number on the number line. But in some textbooks discussing more abstract vector spaces a distinction is needed. there the symbol | | denotes absolute value and || || denotes a norm.
[1.2] (The Geometric norm of position vectors) The following four statements are essential characteristics for the geometric norm.
(a) The geometric norm of a vector is a non-negative real number.
Notation: |p| ≥ 0.
For position vectors this statement is based on the definition that the norm is the length of a segment which is part of the vector, and length is never negative.
(b) The geometric norm of a vector is the number zero if and only if the vector is the zero vector.
Notation: |p| = 0 if and only if p = 0.
For position vectors this statement is based on the fact that a segment has zero length if and only if its end points coincide.
(c) (Triangle inequality) The geometric norm of the sum of two vectors is never larger than the sum of the geometric norms of those two vectors.
Notation: |p + q| ≤ |p| + |q|.
Equality occurs if and only if p and q point in the same direction.
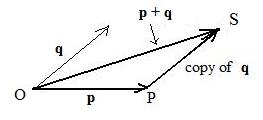
The adjacent figure shows the vector sum OS = p + q and how to get it, using the triangle method, from OP = p and PS = q. The shortest distance from O to S is along p + q. The distance |OP| + |PS| cannot be any shorter.
But if point P is on segment OS so that O is not between P and S, then the length of OS = length of OP + length of PS, that is
|p + q| = |p| + |q|
This happens if and only if position vectors p and q point in the same direction.
(d) The geometric norm of a product of a real number and a vector is equal to the product of the absolute value of the real number and the geometric norm of the vector.
Notation: |λ p| = |λ| |p|
This equality comes directly from the physical definition of multiplying a geometric vector by a real number. The length of the resulting vector is the product of the real number, ignoring the sign, and the length of the original vector.
***
The discussion now focuses on arrays. Here vectors p,q,r will equal arrays.
Recall the special notation for arrays:
for arrays of size 2: array = (x,y), arrayn = (xn, yn), n=1,2,3,...
for arrays of size 3: array = (x,y,z), arrayn = (xn, yn, zn), n=1,2,3,...
Here p = array1 and q = array2 for arrays of either size.
It will be convenient to have a special product for arrays. The following is a definition.
[1.3] (Dot product) The dot product of two arrays is the sum of the products of all corresponding (numerical) coordinates.
Notation: p⋅q = array1⋅array2
= product of first coordinates of both arrays + product of second coordinates of both arrays (+ product of third coordinates of both arrays)
For example,
if p = (5,2), q = (4,-3), then p⋅q = (5,2)⋅(4,-3) = (5)(4) + (2)(-3) = 20 − 6 = 14,
if p = (-6,1,3), q = (2,3,4), then p⋅q = (-6)(2) + (1)(3) + (3)(4) = -12 + 3 + 12 = 3.
The dot product always produces a number, never another array.
The dot product will be developed extensively in Section 2 below.
There is another product, called the cross product, discussed in chapter 6.
In making graphs of points in elementary algebra there is a distance formula. For distance between the origin O and a point P with coordinates:
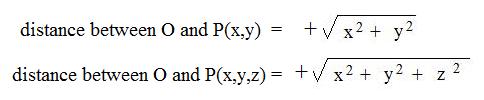
Let p = array of size 2 or size 3.
[1.4] (Algebraic norm for arrays) The norm of an array is the non-negative square root of the sum of squares of all of its coordinates:
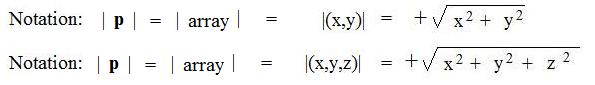
For technical reasons it is difficult to construct the sign of the square root for printing. For discussions here an inline notation sqrt( ) is used. The above notations become:
|p| = |(x,y)| = sqrt(x2 + y2)
or
|p| = |(x,y,z)| = sqrt(x2 + y2 + z2)
Examples:
if p = (3,4) then |p| = |(3,4)| = sqrt(32 + 42) = sqrt(9 + 16) = sqrt(25) = 5.
if q = (1,2,2) then |q| = sqrt(12 + 22 + 22) = sqrt(1 + 4 + 4) = sqrt(9) = 3.
if r = (0,0) then |r| = sqrt(02 + 02) = sqrt(0) = 0.
A way to avoid using any square root sign is to use the squares of norms:
|(x,y)|2 = x2 + y2
|(x,y,z)|2 = x2 + y2 + z2.
A the following is useful in proving statements:
[1.5] (Norms and squares)
(a) For any real number λ, |λ|2 = λ2.
(b) For any real numbers λ,σ, if |λ|2 = |σ|2 then |λ| = |σ|
for any vectors p,q, if |p|2 = |q|2 then |p| = |q|.
(c) The dot product of any array with itself is equal to the square of the norm of that vector: p⋅p = |p|2.
The proof of (c) is trivial: if p = (x,y) then p⋅p = (x,y)⋅(x,y) = xx + yy = x2 + y2 = |(x,y)|2 = |p|2.
A similar chain of equalities exist if p = (x,y,z).
The following inequality reveals the restrictions on how positively large the inner product can become or how negatively small the inner product can become. The inequality is used in many places in mathematics.
[1.6] (Schwarz inequality) The absolute value of dot product of any pair of arrays of the same size cannot exceed the product of the norms of the arrays. Equality occurs if
Nottion: |p⋅q| ≤ |p| |q| where p = array1 and q = array2.
In other words,
|(x1, y1)⋅(x2, y2)| ≤ |(x1, y1)| |(x2, y2)
|(x1, y1, z1)⋅(x2, y2, z2)| ≤
|(x1, y1, z1)| |(x2, y2, z2)|
Equality occurs if the arrays are proportional (parallel)position vectors that locate the points with the arrays as coordinates.
Click here for a computational proof of this last inequality.
Example: Let p = (-3,4), q = (5,-12)
Then |p| = |(-3,4)| = sqrt(9 + 16) = 5, |q| = |(5,-12)| = sqrt(25 + 144) = 13, |p| |q| = (5) (13) = 65.
And |p⋅q;| = |(-3,4)⋅(5,-12)| = |(-3)(5) + (4)(-12)| = |-15 − 48| = |-63| = 63.
Then p⋅q < |p| |q| because 63 < 65.
For [1.7] below consider arrays of size 2 and size 3 without any geometric interpretation. Then the parts (a) - (d) will be proven conclusively and algebraicly without the use of intuitive pictures of geometric position vectors. Moreover, the statements easily extend to arrays of any positive size. But there, any visual geometric interpretation may be difficult because of the difficulty in drawing segments in dimensions > 3.
[1.7] (Properties of the algebraic norm on arrays) The following four statements are true for the norm:
(a) The norm of an array (see [1.4]) is a non-negative real number.
Notation: |(x,y)| is a real number and |(x,y)| ≥ 0.
Notation: |(x,y,z)| is a real number and |(x,y,z)| ≥ 0.
If a number has two square roots, one positive and one negative, only the positive root is used. Therefore, sqrt( ) always uses the non-negative root of what is in ( ). This makes the norm never negative.
(b) The norm of an array is the real number zero if and only if the array is the zero array.
Notation: |(x,y)| = 0 if and only if (x,y) = (0,0).
Notation: |(x,y,z)| = 0 if and only if (x,y,z) = (0,0,0).
An indirect proof shows that the sum of squares of real numbers is zero if and only if all the numbers are zero. (The squares are never negative.)
(c) (Triangle inequality) The norm of the sum of two arrays is never larger than the sum of the norms of those two arrays.
Notation: |(x1,y1) + (x2,y2)| ≤
|(x1,y1)| + |(x2,y2)|.
Notation: |(x1,y1,z1) + (x2,y2,z2)| ≤
|(x1,y1,z1)| + |(x2,y2,z2)|.
Click here to see a proof that uses the Schwarz inequality.
(d) The norm of a product of a real number and an array is equal to the product of the absolute value of the real number and the norm of the array.
Notation: |λ(x,y)| = |λ| |(x,y)|.
Notation: |λ(x,y,z)| = |λ| |(x,y,z)|.
The proof here is done with the squares of norms.
|λ(x,y)|2 = |(λx,λy)|2 = (λx)2 + (λy)2 = (λ)2(x2) + (λ)2(x2 + y2) = |λ|2|(x,y)|2.
Therefore, |λ(x,y)|2 = |λ|2|(x,y)|2.
Take the square root of both sides to get |λ(x,y)| = |λ| |(x,y)|.
.
A similar proof exists for |λ(x,y,z)| = |λ| |(x,y,z)|.
There are other norms on arrays, but they may not relate to familiar geometric properties. Unless the norm is defined otherwise, in discussions of a norm when arrays are involved, the norm is the one defined in [1.4]. The norm for geometric position vectors was defined in [1.1].
***
Perpendicularity is an important idea in geometry. (Another word for perpendicular is orthogonal.) So define geometrically two position vectors being perpendicular or orthogonal if and only if their segments are perpendicular. If coordinates are involved then the dot product can be used to determine perpendicularity.
[1.8] (Perpendicular position vectors) Two non-zero vectors locating points with array coordinates are perpendicular if and only if the dot product of those arrays is zero.
Notation: If position vectors p,q locate points P(x1, y1) and Q(x2, y2) then p,q are perpendicular if and only if p⋅q = x1x2 + x1x2 = 0.
Notation: If position vectors p,q locate points P(x1, y1, z1) and Q(x2, y2, z2) then p,q are perpendicular if and only if p⋅q = x1x2 + y1y2 + z1z2 = 0.
Click here to see a proof for arrays of size 2.
Examples:
If p = (3,4) and q = (4,-3) then p,q are perpendicular because p⋅q = (3)(4) + (4)(-3) = 12 − 12 = 0.
If p = (1,-2,3) and q = (4,2,0) then p,q are perpendicular because p⋅q = (1)(4) + (-2)(2) + (3)(0) = 4 − 4 + 0 = 0.
A collection of vectors is orthogonal if all vectors are non-zero and mutually orthogonal.
The collection of vectors {i,j,k} where
i = (1,0,0), j = (0,1,0), k = (0,0,1)
is orthogonal because the vectors are mutually perpendicular, i.e. the dot product of any two of them is trivially zero.
***
The following definition is true for geometric position vectors and algebraic array vectors.
[1.9] (Unit vector) If the norm of a vector is equal to 1, then that vector is called a unit vector.
Notation: A vector e is a unit vector if and only if |e| = 1.
For example, if position vector e locates the point (3/5, 4/5) then e is a unit vector because |e|2 = (3/5)2 + (4/5)2 = 9/25 + 16/25 = 25/25 = 1. So |e| = 1.
In a plane, unit position vectors locate points on a circle of radius 1 with center at the origin. In space, they locate points on a sphere of radius 1 with center at the origin.
In the plane, the vectors i = (1,0) and j = (0,1) are unit vectors along the x-axis and along the y-axis respectively. Also the lincomb
xi + yj locates the point (x,y)
because xi + yj = x(1,0) + y(0,1) = (x,0) + (0,y) = (x,y).
In space, all the vectors i = (1,0,0), j = (0,1,0), k = (0,0,1) are unit vectors in space along the x-axis, along the y-axis and along the z-axis respectively. Also, the lincomb
xi + yj + zk locates the point (x,y,z).
Trivially, a vector is a unit vector if and only if the dot product of the vector with itself is 1.
Sometimes it is desirable to construct a unit vector from a given non-zero position vector such that the unit vector and position vector point in the same direction. Let λ = 1/p| where p is any non-zero position vector.
Then λ > 0 and λp is a vector pointing in the same direction as p.
Also λp is a unit vector because by [1.6d] |λp| = |λ| |p| = |1/|p| |p| = |p|/|p| = 1.
So the construction is to divide a non-zero vector by its norm.
Example: Suppose the position vector p locates the point (3,4). Then p is not a unit vector because the norm of its square is not 1:
norm2 |p|2 = 32 + 42 = 25.
So |p| = 5. Then p/|p| locates the point (3/5,4/5). Its norm is 5/5 = 1. Therefore, p/|p| is a unit vector.
[1.10] (Normalize a vector) To normalize a non-zero vector is to divide it by its length. The result is a unit vector.
Again suppose the position vector p locates the point (3,4). Then |p| = 5. Then normalizing the expressions on booth sides of the equation, p/5 = 1. So p/5 is a unit vector. Normalizing a vector produces a unit vector that points in the same direction.
It is not possible to normalize the zero vector, because that would require a division by zero.
The basic definition of an geometric vector is that it has the length of a segment and a direction in which one end of the segment points. For any non-zero vector p,
p = |p|e
where e is the unit vector pointing in the same direction as p.
So |p| supplies the length of p and e = p|/|p| supplies the direction of vector p.
***
The parallelogram appears in many discussions about geometric vectors. There is a theorem from plane geometry that gives a relationship involving the lengths of all segments in a parallelogram.
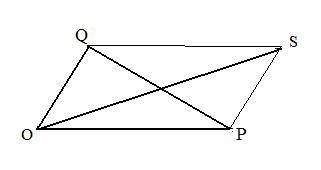 [1.11] (Parallelogram law) The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of all the sides.
[1.11] (Parallelogram law) The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of all the sides.
Notation: In the adjacent figure, |OS|2 + |PQ|2 = |OP|2 + |PS|2 + |SQ|2 + |QO|2
Click here to see a proof of [1.11] using only methods of plane geometry.
[1.12] (Parallelogram law for norms of position vectors and algebraic arrays) For any vectors p,q,
|p + q|2 + |p − q|2 = 2|p|2 + 2|q|2.
For geometric position vectors:
In the notation for [1.11] replace |OS| by |p + q|, |PQ| by |p − q|, |OP| by |p|, |PS| by |q|, |SQ| by |p|, |QO| by |q| and collect like terms.
The norm for geometric position vectors ([1.1]) satisfies [1.12] because [1.11] was proven by methods of plane geometry.
For algebraic arrays:
Let p and q locate points P(x1, y1) and Q(x2, y2). By definition the square of the norms of arrays = sum of the squares of all of the coordinates. Then the norms of p, q, p+q, p − q are
|p|2 = (x1)2 + (y1)2,
|q|2 = (x2)2 + (y2)2,
|p + q|2 = (x1 + x2)2 + (y1 + y2)2 =
(x1)2 + 2(x1)(x2) + (x2)2 +
(y1)2 + 2(y1)(y2) + (y2)2
|p − q|2 = (x1 − x2)2 + (y1 − y2)2 =
(x1)2 − 2(x1)(x2) + (x2)2 +
(y1)2 − 2(y1)(y2) + (y2)2
Adding the last two equations produces:
|p + q|2 + |p − q|2 = 2(x1)2 + 2(y1)2 = 2|p|2 + 2|q|2
A similar proof exists for arrays of size 3:
|p + q|2 + |p − q|2 = 2(x1)2 + 2(y1)2 + 2(z1)2 = 2|p|2 + 2|q|2
The norm for algebraic array vectors ([1.4]) satisfies [1.12].
But not all norms satisfy [1.12]. It is possible to construct some "weird" norms that satisfy all four axioms for a norm [1.2], but do not satisfy the parallelogram law [1.12]. An example is given in the next chapter.
Section 2: More about the dot product
There are six fundamental properties of the dot product defined in [1.3] for arrays.
[2.1] (Fundamental properties of the dot product of arrays) There are six defining properties properties for the dot product of arrays.
Let
p = array1, q = array2, r = array3 so that
p⋅q = array1⋅array2 ..... etc
(a) The dot product of arrays is a real number
Notation: p⋅q is a real number
(b) The dot product of an array with itself is a non-negative real number.
Notation: p⋅p ≥ 0
(c) The dot product of an array with itself is zero if and only if the array is the zero array.
Notation: p⋅p = 0 if and only if p = 0
(d) The dot product of arrays is commutative.
Notation: p⋅q = q⋅p
(e) The dot product of arrays is distributive.
Notation: p⋅(q + r) = p⋅q + p⋅r.
(f) A scalar may be factored out of the dot product.
Notation: (λp)⋅q = λ(p⋅q).
These statements are not difficult to prove, most using the axioms for arrays as given in Chapter 2 of this volume. For example,
if the discussion involves arrays of size 2, then for part (b),
array1⋅array1 = (x1,y1)⋅(x1,y1) = x1x1 + y1y1
= (x1)2 + (y1)2
which is never negative, because it is a sum of squares of real numbers.
A similar proof can be made for arrays of size 3.
Click here to see proofs of the other statements in [2.1].
The following equations are useful in some of the following discussions. Many of them are very similar to equations studied in elementary algebra, and multiplied out in the same way. Actually, that multiplying out is using the properties listed in [2.1].
[2.2] (Useful equations)
(a) (p + q)⋅(r + s) = p⋅r + p⋅s + q⋅r + q⋅s
(b) (p + q)⋅(r − s) = p⋅r − p⋅s + q⋅r − q⋅s
(c) (p + q)⋅(p − q) = |p|2 − |q|2
(d) |p + q|2 = |p|2 + 2p⋅q + |q|2
(e) |p − q|2 = |p|2 − 2p⋅q + |q|2
(f) λp⋅(αa + βb + γc + δd) =
λαp⋅ + λβp⋅b + λγp⋅c + λδp⋅d.
[extended distributive law]
Click here to see the proofs of these equations. The proofs are based on the properties listed in [2.1]and do not involve arrays directly.
Notice that adding equations (d) and (e) together produces the parallelogram law in [1.12].
The dot product has applications to geometry (and to physics). Often figures can be drawn to give visual support to expressions involving the dot product.
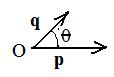 [2.3] (Geometric interpretation of the dot product) The dot product of two position vectors is equal to the product of their lengths and the cosine of the angle between them.
[2.3] (Geometric interpretation of the dot product) The dot product of two position vectors is equal to the product of their lengths and the cosine of the angle between them.
Notation: p⋅q = |p| |q| cos θ, where θ is the angle between p and q.
This interpretation will be called the "geometric dot protuct."
Click here to see a derivation of geometric dot product from the algebraic dot product of two arrays. Therefore, the two dot products are equivalent because they always produce equal (numerical) results. However, often one dot product may be easier to evaluate or to apply than the other dot product.
Example1
If p and q are position vectors of lengths 4 and 6 respectively, and the angle between them is 60° then their geometric dot product is:
p⋅q = (4)(6)cos 60° = 24(1/2) = 12.
It would be difficult to apply the dot product of arrays to the evaluation of the given data.
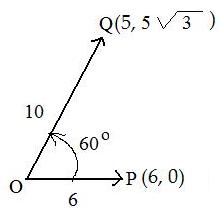
Example2
In the adjacent figure are two position vectors, p = OP and q = OQ of lengths 6 and 10 respectively. The angle between them is 60° The position vectors locate points P(6,0) and Q(5,5sqrt(3)) respectively. Both dot products are computed.
geometric dot product of position vectors: p⋅q = OP⋅OQ = (6)(10) cos 60° = 60 (1/2) = 30
algebraic dot product of arrays : p⋅q = (6,0)⋅(5,5sqrt(3) = (6)(5) + (0)(5sqrt(3)) = 30
The two dot products always produce equal results.
In [1.8] perpendicularity was discussed using dot product = 0 for arrays. But it is often more natural to use the geometric dot product, because the included angle θ = 90° for perpendicularity of position vectors, where cos 90° = 0.
Exmple3
The Schwarz inequality [1.6] can be easily proven using the geometric dot product, because |cos θ| &le 1 . Click here to see the simple argument.
Example4
Although the equation [2.2c]
(p + q)⋅(p − q) = |p|2 − |q|2
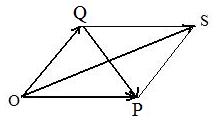 was proven using properties listed in [2.1] based on arrays, it does have an interesting geometric interpretation. It is based on the fact that if either side of equation is equal to zero then the other side must be equal to zero.
was proven using properties listed in [2.1] based on arrays, it does have an interesting geometric interpretation. It is based on the fact that if either side of equation is equal to zero then the other side must be equal to zero.
Let position vectors p, q and p + q locate points P,Q,S in the addition parallelogram OPSQ (see adjacent figure).
Therefore, diagonal vector OS = p + q and diagonal vector QP = p − q are perpendicular (left side of equation = 0) if and only if |p| = |q| (right side =0).
This last statement |p| = |q| makes all four sides of the parallelogram have equal length, which is the definition of a rhombus. Therefore,
the diagonals of a parallelogram are perpendicular (left side of equation = 0) if and only if the parallelogram is a rhombus (right side of equation = 0).
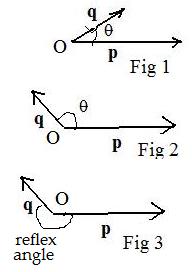
Actually, there are two angles between two non-zero position vectors. One is 0 ≤ θ ≤ 180°. (Fig 1 and Fig 2) . The other is between 180° and 360°. (Fig 3). The angle between two position vectors is always chosen to be between 0° and 180° inclusively. (Fig 1 and Fig 2) .
The orientation of the angle is not important. It can be measured from p to q or from q to p. The geometric dot product is the same because cos (-θ) = cos θ.
Because the geometric dot product is equivalent to the algebraic dot product of arrays, the geometric dot product obeys the six properties listed in [2.1]. Simply change the wording: ignore the equalities of position vectors to arrays and replace "arrays" with "geometric position vectors." The first four properties can be proven directly using the geometric definition. For example the following proves (b):
p⋅q = |p| |q| cos θ = |q| |p| cos θ = q⋅p
Very subtly, the fact that the orientation of the angle θ is not important was used where the equality was red (=).
Recall that a linear combination (lincomb) of vectors and real number coefficients is linearly independent if and only if setting the lincomb to equal zero forces all the coefficients to be zero. The extended distributive law [2.2f] is used to prove the following:
[2.4] (Orthogonality and linear independence) The linear combination of any collection of non-zero orthogonal vectors is linearly independent.
Let p,q,r be a collection of non-zero orthogonal position vectors. (It is possible to involve fewer or more vectors.) Form a lincomb of them
(lincomb) αp + βq + γr
and set it to zero:
(lincomb = 0) αp + βq + γr = 0
Form the dot product of p and this lincomb:
(p⋅lincomb) p⋅(αp + βq + γr) = p⋅0
Use the distributive law:
αp⋅p + βp⋅q + γp⋅r = 0
which results in the equation (because the vectors are orthogonal):
α|p|2 + 0 + 0 = 0
Simplifying,
α|p|2 = 0
Since p is a non-zero vector, α must equal zero.
Similar inner products of q and r with lincomb show
β|q|2 = 0 and γ|r|2 = 0
Hence all three coefficients α, β γ are forced have only the value zero.
Therefore, the only lincomb of p,q,r equal to the zero vector is the trivial lincomb. This makes p,q,r linearly independent.
Example:
The orthonormal vectors i,j,k were discussed earlier. The lincomb xi + yj + zk locates the point (x,y,z). [2.3] says that it is the only lincomb of i,j,k to locate that same point. To see this, let x'i + y'j + z'k also locates that same point. Then
xi + yj + zk = x'i + y'j + z'k
This means that upon subtraction:
(x − x')i + (y − y')j + (z − z')k = 0
But the vectors i,j,k are linearly independent. By [2.3] the coefficients must be equal to zero:
x − x' = 0, y − y' = 0, z − z' = 0
This means that the two lincombs
xi + yj + zk, x'i + y'j + z'k
are identical, including their coefficients.
 The geometric interpretation of dot product supports the idea of a position vector p orthogonally projected upon a line through the origin. Let P be the point located by p. Drop P perpendicularly to the line onto the line, making a point P'. Then OP' is the projected image of p = OP onto the line. The vector OP' is called the component of p = OP along the line.
The geometric interpretation of dot product supports the idea of a position vector p orthogonally projected upon a line through the origin. Let P be the point located by p. Drop P perpendicularly to the line onto the line, making a point P'. Then OP' is the projected image of p = OP onto the line. The vector OP' is called the component of p = OP along the line.
If e is a unit vector along the line, then OP' = |OP'|e = (|OP|cos θ)e = (p⋅e)e. This is true even if e and the projected image OP' point in opposite directions.
[2.5] (Component of a vector) If a position vector is projected orthogonally onto a line through the origin then the result is the component of that vector along the line.
Notation: if p is any position vector and e is any unit vector along a line through the origin, then (p⋅e)e is the component along the line.
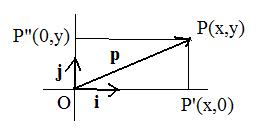 The vectors i and j are unit vectors along the x-axis and y-axis in elementary algebra. For any position vector p locating point P(x,y),
The vectors i and j are unit vectors along the x-axis and y-axis in elementary algebra. For any position vector p locating point P(x,y),
If a position vector p is projected orthogonally onto the x-axis and onto the y-axis ptoducing components OP' and OP", then
OP' = (p⋅i)i = xi and OP" = (p⋅j)j = yj
are the projections respectively onto these axes. A similar situatiuon exists in space with the projection of p onto the x-axis, y-axis and z-axis respectively. Simply include OP'" = (p⋅k)k = zk in the list of orthogonally projected images onto the 3 axes.
++++++++++++++++++++++++
The following is useful in some discussions below.
[2.5] (Difference of squares) The inner product of the sum and the difference of two vectors is equal to the difference of squares of their norms:
Notation: (p + q)⋅(p − q) = |p|2 − |q|2
By simple algebra, (p + q)⋅(p − q) = p⋅p − q⋅q By [2.3] this last expression can be converted to a difference of squares of norms.
 The equation
The equation
(#) (p + q)⋅(p − q) = |p|2 − |q|2
has a geometric interpretation. The sum and differences
p + q and p − q
are vectors along the diagonals OS and QP of a parallelogram OPSQ (see adjacent figure), and
|p| and |q|
are lengths |OP| aand |OQ| of two adjacent sides.
If either side of the equation (#) is zero then the other side must be zero. This means that the diagonals of a parallelogram are perpendicular if and only if the parallelogram has two adjacent sides of equal length, which means that the parallelogram is a rhombus (all four sides have equal length).
Simple algebra proves the following equations which are extensions of the distributive law for inner products:
[2.6] Useful equations:
(a) (p + q)⋅(r + s) = p⋅r + p⋅s + q⋅r + q⋅s
(b) (p + q)⋅(r − s) = p⋅r − p⋅s + q⋅r − q⋅s
(c) |p + q|2 = |p|2 + 2p⋅q + |q|2
(d) |p − q|2 = |p|2 − 2p⋅q + |q|2
Equation (d) is equivalent to the law of cosines for a triangle.
Notice that adding the equations in (c) and (d) produces the equation in [1.11]. Therefore, every norm produced by an inner product (see [2.3]) satisfies the parallelogram law [1.11].
***
The dot product was defined in the discussion just before Section 1 above. It shall be known as the algebraic definition of inner product (involving arrays).
Using both definitions for inner product, geometric ([2.1]) and algebraic, it is possible to find the angle between two position vectors locating points with coordinates. For example, to find the angle between position vectors locating points (2,3) and (4,5):
geometric inner product = |(2,3)| |(4,5)| cos θ = sqrt(13)sqrt(41)cos θ = sqrt(533) cos θ
algebraic inner product = (2)(4) + (3)(5) = 23.
So sqrt(533) cos θ = 23.
Therefore, cos θ = 23/sqrt(533) = 23/(23.08679) = 0.9962+ , So θ = 5° (approximately). Intuitively speaking, the position vectors from the origin to (2,3) and origin to (4,5) almost point in the same direction, because the angle between them is very small.
In [2.2] six basic properties of a geometric inner product were listed. There are six correesponding properties of the algebraic inner product of arrays. Now let position vectors denote arrays:
p = array1, q = array2, r = array3.
Then [2.2] becomes the following:
[2.7] (Fundamental properties of the inner product of arrays) There are six defining properties properties for the inner product of arrays:
(a) The inner product of arrays is a real number (not an array): p⋅q = array1⋅array2 is a real number.
(b) The inner product of an array with itself is a non-negative real number: p⋅p = array1⋅array1 ≥ 0
(c) The inner product of an array with itself is zero if and only if the array is the zero array:
p⋅p = array1⋅array1 = 0 if and only if p = array1 = 0 (zero array)
(d) The inner product of arrays is commutative: p⋅q = array1⋅array2 = array2⋅array1 = q⋅p
(e) The inner product of arrays is distributive: p⋅(q + r) = array1⋅(array2 + array3) = array1⋅array2 + array1⋅array3 = p⋅q + p⋅r.
(f) A scalar may be factored out of the inner product: (λp)⋅q = (λarray1)⋅array2 = λ(array1⋅array2) = λ(p⋅q).
These statements are not difficult to prove, most using the axioms for arrays as given in Chapter 2 of this volume. For example,
if the discussion involves arrays of size 2, then for part (b),
array1⋅array1 = (x1,y1)⋅(x1,y1) = x1x1 + y1y1
= (x1)2 + (y1)2
which is never negative, because it is a sum of squares of real numbers.
A similar proof can be made for arrays of size 3.
Click here to see proofs of the other statements in [2.7].
***
The inner product makes it easier to verify that a collection of vectors are orthogonal or even orthonormal.
Example. Verify that position vectors p,q,r locating points (1,-8,-4), (-8,1,-4), (4,4,-7) form an orthogonal collection.
p⋅q = (1,-8,-4)⋅(-8,1,-4) = (1)(-8) + (-8)(1) + (-4)(-4) = -8 + (-8) + 16 = 0
p⋅r = (1,-8,-4)⋅(4,4,-7) = (1)(4) + (-8)(4) + (-4)(-7) = 4 + (-32) + 28 = 0
q⋅r = (-8,1,-4)⋅(4,4,-7) = (-8)(4) + (1)(4) + (-4)(-7) = -32 + 4 + 28 = 0
Because |p| = |q| = |r| = 9, all three vectors can be normalized by a division by 9. Therefore, p/9, q/9, r/9 form an orthonormal collection.
Often the vectors p,q,r will be used with arrays array1, array2, array3. Instead, the phrases
p locates the point P(array1), q locates the point Q(array2), ...and in space...
r locates the point R(array3)
or simply
p = array1, q = array2 ...and in space... r = array3
will be used. So arrays serve the dual purpose of being vectors and being coordinates locating points.
***
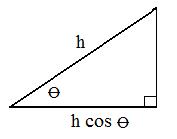
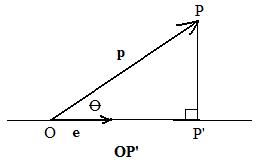
Recall from trigonometry how the cosine of an angle θ is involved with a right triangle. The product of the hypotenuse h and cos θ is equal to the length of the side adjacent to θ, as shown in the adjacent figure.
 Now consider two position vectors p and e, where e is a unit vector. Through e draw a line. See adjacent figure. From point P, located by position vector p, drop a perpendicular to the line to locate a point P' on the line. Then in right triangle OPP', length OP' = |p| cos θ But by definition of inner product, p⋅e = |p| |e| cos θ = |p| (1) cos θ = OP'.
Now consider two position vectors p and e, where e is a unit vector. Through e draw a line. See adjacent figure. From point P, located by position vector p, drop a perpendicular to the line to locate a point P' on the line. Then in right triangle OPP', length OP' = |p| cos θ But by definition of inner product, p⋅e = |p| |e| cos θ = |p| (1) cos θ = OP'.
[2.10a] (Orthogonal projection and inner product) The inner product of a position vector and a unit vector produces the length of the orthogonal projection of the vector onto the line through the unit vector if the angle between them is acute, and minus the length of the projection onto the line if the angle is obtuse.
Notation: if p and e are position vectors where e is a unit vector, then p⋅e is the length of the projection on a line parallel to e, if the angle θ between the vectors is acute (0° ≤ θ ≤ 90°), and minus the length if the angle θ is obtuse (90° ≤ θ ≤ 180°)
In the figure OP' is a line segment. However, a vector OP' can be from of it. It is parallel to the unit vector e. If 0° ≤ θ ≤ 90° then point P' falls to the right of the unit vector, and the vector OP' and e have the same direction. But if 90° ≤ θ ≤ 180° then P' falls to the left of the unit vector, and OP' and e have opposite directions.
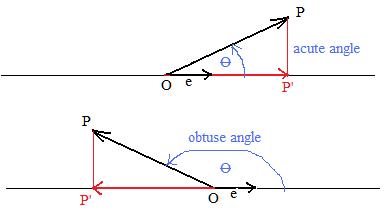
[2.10b] (Component along a unit vector) If the unit vector is part of the inner product mentioned in [2.10a] then a vector is obtained parallel to the unit vector by attaching the unit vector to the inner product. It is called a component of the original vector along the line containing the unit vector.
Notation: if p = OP and e are position vectors where e is a unit vector, then (p⋅e)e = OP' = component (position vector) of p along the line through e.
Notice that the component and the unit vector e have the same direction if the angle θ is acute, and opposite directions if the angle θ is obtuse.
If position vector p locates the point (x,y) then p = xi + yj and p⋅i = x, p⋅j = y, and (p⋅i)i = xi is the component of p along the x-axis containing the unit vector i, and (p⋅j)j = yj is the component of p along the y-axis containing the unit vector j.
If p locates the point (x,y,z) then
p = xi + yj + zk
and in addition p⋅k = z. Here (p⋅k)k = zk is the component of p along the z axis containing the unit vector k.
***
For any angle θ, cos θ always lies between -1 and +1. In other words, |cos θ| ≤ 1. Then taking absolute values of both sides of the geometric definition of inner product p⋅q = |p| |q| cos θ produces |p⋅q| = |p| |q| |cos θ| . Because |cos θ| ≤ 1 the right side of the equation is less than or equal to |p| |q|.
|p⋅q| = |p||q||cos θ| ≤ |p||q|(1) = |p||q
This discussion gives support to the following:
The geometric definition of the inner product involves the angle between two vectors, and the cosine of that angle. For all angles the cosine isbetween +1 and −1. All this can be summed up as |cos θ| ≤1. Then
(*)
|p⋅q| = |p||q||cos θ| ≤ |p||q|(1) = |p||q
his discussion gives support to the following:
[2.11a] (Schwarz inequality) The absolute value of the inner product of two vectors is less than or equal to the product of their norms.
Notation: |p⋅q| ≤ |p| |q
The expression (*) plays a key role in establishing the Sehwarz inequality. But equality occurs when cos θ is 1 or -1. This happens only when θ is 0° or 180° Geometrically, that is when the vectors are parallel, pointing in the same or opposite directions.
[2.11b] (Equality in the Schwarz inequality) The absolute value of the inner product of two vectors is equal to the product of their norms if and only if one or both vectors are zero or the vectors are parallel.
Notation: |p⋅q| = |p| |q| if and only if p = 0 or q = 0 or p and q are parallel.
 If the shortest distance between two points A and B is the length of the segment joining the points, then the distance is longer if a third point C is off of the segment AB and the measuring process between A and B is done by going through C, as shown in the adjoining figure. This fact can be demonstrated by an expression with a strict inequality symbol:
If the shortest distance between two points A and B is the length of the segment joining the points, then the distance is longer if a third point C is off of the segment AB and the measuring process between A and B is done by going through C, as shown in the adjoining figure. This fact can be demonstrated by an expression with a strict inequality symbol:

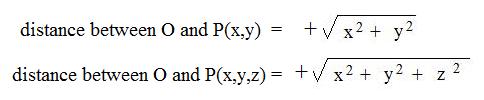
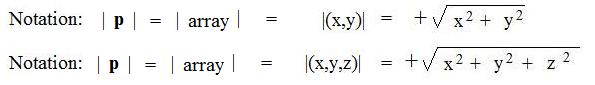
 [1.11] (Parallelogram law) The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of all the sides.
[1.11] (Parallelogram law) The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of all the sides.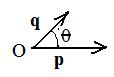 [2.3] (Geometric interpretation of the dot product) The dot product of two position vectors is equal to the product of their lengths and the cosine of the angle between them.
[2.3] (Geometric interpretation of the dot product) The dot product of two position vectors is equal to the product of their lengths and the cosine of the angle between them.
 was proven using properties listed in [2.1] based on arrays, it does have an interesting geometric interpretation. It is based on the fact that if either side of equation is equal to zero then the other side must be equal to zero.
was proven using properties listed in [2.1] based on arrays, it does have an interesting geometric interpretation. It is based on the fact that if either side of equation is equal to zero then the other side must be equal to zero.
 The geometric interpretation of dot product supports the idea of a position vector p orthogonally projected upon a line through the origin. Let P be the point located by p. Drop P perpendicularly to the line onto the line, making a point P'. Then OP' is the projected image of p = OP onto the line. The vector OP' is called the component of p = OP along the line.
The geometric interpretation of dot product supports the idea of a position vector p orthogonally projected upon a line through the origin. Let P be the point located by p. Drop P perpendicularly to the line onto the line, making a point P'. Then OP' is the projected image of p = OP onto the line. The vector OP' is called the component of p = OP along the line. The vectors i and j are unit vectors along the x-axis and y-axis in elementary algebra. For any position vector p locating point P(x,y),
The vectors i and j are unit vectors along the x-axis and y-axis in elementary algebra. For any position vector p locating point P(x,y),