Return to main page
Additional Material D4
Square roots
Every positive real number has a positive square root. For example,
the square root of 16 is 4, the square root of 49 is 7, the square root of 4/9 is 2/3.
In discussions here the phrase "the square root of" is abbreviated as "sqrt". So that
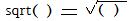 sqrt(16) = 4, sqrt(49) = 7, sqrt(4/9) = 2/3.
Also sqrt(0) = 0. (The symbol sqrt is called the inline notation for square root, and is used in writing square roots in some computer programming languages.)
sqrt(16) = 4, sqrt(49) = 7, sqrt(4/9) = 2/3.
Also sqrt(0) = 0. (The symbol sqrt is called the inline notation for square root, and is used in writing square roots in some computer programming languages.)
Often expressions must be evaluated before the square root is taken.
sqrt(32 + 42) = sqrt(9 + 16) = sqrt(25) = 5.
sqrt((7 − 2)2 + (15 − 3)2) = sqrt(52 + 122) = sqrt(25 + 144) = sqrt(169) = 13.
It may be more read|AB|le if the square root notation is not used so often.
Let U = sqrt(32 + 42).
Then
U2 = 32 + 42 = 9 + 16 = 25. U = sqrt(25) = 5.
Similarly,
Let V = sqrt((7 − 2)2 + (15 − 3)2).
Then
V2 = (7 − 2)2 + (15 − 3)2 = 52 + 122 = 25 + 144 = 169. V = sqrt(169) = 13.
Derivation of law of Cosines
Let θ be the angle between two sides OP and OQ of a triangle OPQ. Then
\QP|2 = |OP|2 + |OQ|2 − 2|OP| |OQ| cos θ.
There are two cases where points O,P,Q are not collinear. In both cases drop a line from Q perpendicular to line OP and meeting it at T.
Case I: 0° < θ ≤ 90° Fig 1
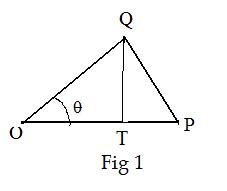 Then cos θ ≥ 0.
Then cos θ ≥ 0.
(1) |OT| = |OQ| cos θ
Now in right triangles PTQ and OTQ apply the Pythagorean theorem:
|QP|2 = |TP|2 + |QT|2
|OQ|2 = |OT|2 + |QT|2
Subtraction of these two equations eliminates |QT|:
(2) |QP|2 − |OQ|2 = |TP|2 − |OT|2
To eliminate |TP| notice that
|TP| = |OP| − |OT|
Squaring both sides produces
|TP|2 = |OP|2 − 2 |OP| |OT| + |OT|2
Replacing |TP|2 in equation (2) by the right side of this equation produces
|QP|2 − |OQ|2 = |OP|2 − 2 |OP| |OT| + |OT|2 − ||OT|2
Simplifying and solving for |QP|2 produces
|QP|2= |OP|2 + |OQ|2 − 2 |OP| |OT|
Eliminate |OT| by replacing it in this equation by the right side of (1) above
(*) |QP|2= |OP|2 + |OQ|2 − 2 |OP| |OQ| cos θ
Case I: 90° < θ < 180° Fig 2
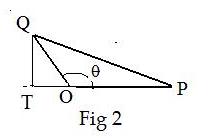 Then cos θ ≤ 0. Hence (− cos θ) ≥ 0
Then cos θ ≤ 0. Hence (− cos θ) ≥ 0
(3) |OT| = |OQ| (−cos θ)
Now in right triangles PTQ and OTQ apply the Pythagorean theorem:
|QP|2 = |TP|2 + |QT|2
|OQ|2 = |OT|2 + |QT|2
Subtraction of these two equations eliminates |QT|:
(4) |QP|2 − |OQ|2 = |TP|2 − |OT|2
To eliminate |TP| notice that
|TP| = |OP| + |OT|.
Squaring both sides produces
|TP|2 = |OP|2 + 2 |OP| |OT| + |OT|2
Replacing |TP|2 in equation (4) by the right side of this equation produces
|QP|2 − |OQ|2 = |OP|2 + 2 |OP| |OT| + |OT|2 − |OT|2
Simplifying and solving for |QP|2 produces
|QP|2 = |OP|2 + |OQ|2 + 2 |OP| |OT|
Eliminate |OT| by replacing it by the right side of (#). The result is again equation
(*) |QP|2= |OP|2 + |OQ|2 − 2 |OP| |OQ| cos θ
If O,P,Q are collinear then there are three cases to consider:
θ = 0°: Q is between O and P,
θ = 0°: P is between O and Q
θ = 180°: O is between Q and P.
The proofs consist simply of adding and subtracting segments OQ, PQ to get PQ and inserting the squares their lengths into (*). The reader can supply the details.
Derivation of the geometric interpretation of the dot product
 The dot product was originally defined for arrays only. There is a geometric interpretation of this dot product that involves position vectors, their lengths and the angle between them. No arrays are involved in this interpretation.
Figure A shows a simple triangle OPQ. Figure B shows a congruent triangle with vectors p, q, QP as sides and arrays as coordinates:
The dot product was originally defined for arrays only. There is a geometric interpretation of this dot product that involves position vectors, their lengths and the angle between them. No arrays are involved in this interpretation.
Figure A shows a simple triangle OPQ. Figure B shows a congruent triangle with vectors p, q, QP as sides and arrays as coordinates:
P(x1, y1) and Q(x2, y2).
The basic idea is to measure side QP in Fig A using the law of cosines (see above for a derivation of this law) and the length of vector QP in Fig B:
(a) (Law of cosines)
|QP|2 = |OP|2 + |OQ|2 − 2 |OP| |OQ| cos θ
(b) (Square of the norm of a vector) |QP|2 = |p − q|2 =
| (x1 − x2)2 + (y1 − y2)2
=
x12 + y12 + x22 + y22 − 2(x1x2 + y1y2)
=
|p|2| + |q|2 − 2p⋅q
But |QP| = |QP| because the triangles are congruent. So
|OP|2 + |OQ|2 − 2 |OP| |OQ| cos θ =
|p|2| + |q|2 − 2p⋅q
But |OP| = |p|, |OQ| = |q|. Therefore,
|p|2 + |q|2 − 2 |p| |q| cos θ = |p|2| + |q|2 − 2p⋅q
Eliminate like terms from both sides and divide the result by −2, to produce the desired result:
&nbp; |p| |q| cos θ = p⋅q.
A similar proof exists for points O,P,Q is space:
P(x1, y1, z1) and Q(x2, y2, z2)
also lead to
|p| |q| cos θ = p⋅q.
Proof of the following equations
(a) (p + q)⋅(r + s) = p⋅r + p⋅s + q⋅r + q⋅s
(b) (p + q)⋅(r − s) = p⋅r − p⋅s + q⋅r − q⋅s
(c) (p + q)⋅(p − q) = |p|2 − |q|2
(d) |p + q|2 = |p|2 + 2p⋅q + |q|2
(e) |p − q|2 = |p|2 − 2p⋅q + |q|2
(f) λp⋅(αa + βb + γc + δd) =
λαp⋅ + λβp⋅b + λγp⋅c + λδp⋅d.
***
Equation (a) (p + q)⋅(r + s) = (p + q)⋅r + (p + q)⋅s = p⋅r + q⋅r + p⋅s + q⋅s
Equation (b) (p + q)⋅(r − s) =
To show |p |2 + |q |2 − |p − q|2 = 2p⋅q for vector arrays.
Let P(x1, y1) and Q(x2, y2) be the points located by p and q respectively. Replace the vectors on the left side by their arrays and evaluate the norms:
|p |2 + |q |2 − |p − q|2 =
x12 + y12 +
x22 + y22 −
((x1 − x2)2 + (y1 − y2)2) =
x12 + y12 +
x22 + y22 −
(x12 − 2x1x2 + x22 +
y12 − 2y1y2 + y22) =
2x1x2 + 2y1y2 =
2p⋅q
A similar proof exists for arrays of size 3, where P(x1, y1, z1) and Q(x2, y2, z1) are the points located by p and q respectively.
The Geometric Norm on Position Vectors
(a) The norm of vector is a non-negative real number.
Notation. |p| ≥ 0 for any position vector or array
For position vectors this statement is based on the definition that the norm is the length of a vector, and length is never negative.
(b) The norm of a vector is zero if and only if the vector is the zero vector
Notation. |p| = 0 if and only if p = 0 for any position vector or array p
For position vectors this statement is based on the fact that a segment has zero length if and only if its end points coincide.
(c) (Triangle inequality) The norm of the sum of two vectors is never larger than the sum of the norms of those two vectors.
Notation. |p + q| ≤ |p| + |q| for any position vectors p and q
Equality occurs if and only if p and q one or both are zero vectors or they point in the same direction.
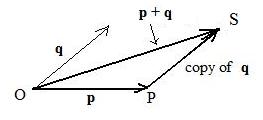 The adjacent figure shows the vector sum OS = p + q and how to get it, using the triangle method, from OP = p and PS = q. The shortest distance from O to S is along p + q. The distance |OP| + |PS| cannot be any shorter.
The adjacent figure shows the vector sum OS = p + q and how to get it, using the triangle method, from OP = p and PS = q. The shortest distance from O to S is along p + q. The distance |OP| + |PS| cannot be any shorter.
But if point P is on segment OS so that O is not between P and S, then the length of OS = length of OP + length of PS, that is
|p + q| = |p| + |q|
This happens if and only if position vectors p and q point in the same direction.
(d) The norm of a product of a scalar and a vector is equal to the product of their individual norms.
|λp| = |λ| |p|
This equality comes directly from the physical definition of multiplying a geometric vector by a real number. The length of the resulting vector is the product of the real number, ignoring the sign, and the length of the original vector.
Proof of the Schwarz inequality for arrays of size 3
(x1, y1, z1)⋅(x2, y2, z2) ≤ |(x1, y1, z1)| |(x2, y2, z2)|
It will be shown that the difference of squares
|(x1, y1, z1)|2 |(x2, y2, z2)|2 −
( (x1, y1, z1)⋅(x2, y2, z2) )2
is never negative.
|(x1, y1, z1)|2 |(x2, y2, z2)|2 −
( (x1, y1, z1)⋅(x2, y2, z2) )2
=
(x12 + y12 + z12)(x12 + y12 + z12) −
(x1x2 + y1y2 + z1z2)2
=
x12x22 + y12y22 + z12z22 +
x12y22 +
x12z22 +
x22y12 +
y12z22 +
x22z12 +
y22z12 −
(x12x22 +
y12y22 + z12z22 +
2x1x2y1y2 +
2x1x2z1z2 +
2y1y2z1z2)
=
x12y22 +
x22y12 +
x12z22 +
x22z12 +
y12z22 +
y22z12
−
2x1x2y1y2 −
2x1x2z1z2 −
2y1y2z1z2
=
x12y22 −
2x1x2y1y2 +
x22y12 +
x12z22 −
2x1x2z1z2 +
x22z12 +
y12z22 −
2y1y2z1z2 +
y22z12
=
(x1y2 − x2y1)2
+
(x1z2 − x2z1)2
+
(y1z2 − y2z1)2
≥ 0.
Therefore,
|(x1, y1, z1)|2 |(x2, y2, z2)|2 −
( (x1, y1, z1)⋅(x2, y2, z2) )2
≥ 0
Hence, |(x1, y1, z1)|2 |(x2, y2, z2)|2
≥
( (x1, y1, z1)⋅(x2, y2, z2) )2
Taking square roots of both sides of the inequality and reversing the inequality produces
|(x1, y1, z1)⋅(x2, y2, z2)| ≤
|(x1, y1, z1)| |(x2, y2, z2)|
But (x1, y1, z1)⋅(x2, y2, z2) ≤
|(x1, y1, z1)⋅(x2, y2, z2)|
and the Schwarz inequality follows.
The inequality
|(x1, y1, z1)⋅(x2, y2, z2)| ≤
|(x1, y1, z1)| |(x2, y2, z2)|
is called in these notes the "super Schwarz inequality: |p⋅q| ≤ |p| |q|. It implies the regular Schwarz inequality.
By removing z's, setting z=0, and modifying appropriately the argument, a proof of (x1, y1)⋅(x2, y2) ≤ |(x1, y1)| |(x2, y2)| for arrays of size 2 is obtained.
Proof of the triangle inequality for arrays of size 3
|(x1 + x2, y1 + y2, z1 + z2)|
≤
|(x1, y1, z1)| + |(x2, y2, z2)|
The following is a proof of the inequality obtained by sqaring both sides:
|(x1 + x2, y1 + y2, z1 + z2)| 2
≤
(|(x1, y1, z1)| + |(x2, y2, z2)|)2
Continuing to male true inequalities using algebra on each side:
(x1 + x2)2 + (y1 + y2)2 + (z1 + z2)2
≤
|(x1, y1, z1)|2 + 2|(x1, y1, z1)| |(x2, y2, z2)| + |(x2, y2, z2)|2
Expanding squares:
x12 + 2x1x2 + x22 +
y12 + 2y1y2 + y22 +
z12 + 2z1z2 + z22
≤
x12 + y12 + z12 +
2|(x1, y1, z1)| |(x2, y2, z2)| +
x22 + y22 + z22
Cancelling like terms on both sides of the inequality:
2x1x2 + +
+ 2y1y2 + +
+ 2z1z2
≤
2|(x1, y1, z1)| |(x2, y2, z2)|
Division by (coefficient) 2 on both sides of the inequality:
x1x2 + +
+ y1y2 + +
+ z1z2
≤
|(x1, y1, z1)| |(x2, y2, z2)|
But this is the Schwarz inequality (see above) and is therefore true. The proof is the reverse of all the steps here.
By removing z's, setting z=0, and modifying appropriately the argument, a proof of
|(x1 + x2, y1 + y2)|
≤
|(x1, y1| + |(x2, y2)|
for arrays of size 2 is obtained.
Triangle equality
The inequality in part c |AB|ove is an equality if and only if either one or both of the vectors are zero or the vectors (are parallel and) point in the same direction.
If |u + v| = |u| + |v| then the one inequality in the chain (#) becomes an equality, namely u⋅u + 2u⋅v + v⋅v = |u|2 + 2|u| |v| + |v|2 which forces u⋅v = |u| |v| . This means that |u| |v| cos θ = |u| |v|. This equality happens if either or both vectors are zero, or when cos θ = 1. Then angle θ = 0, which means that the vectors point in the same direction.
Sums of squares of vector sums and differences
[2.9b] (Sums of squares of vector sums and differences) The sum of the square of the norm of the vector sum and the square of the norm of the vector difference of any two position vectors is equal to twice the sum of the squares of the norms of e|AC|h vector.
Notation:
(#)
|p + q|2 + |p − q|2 = 2(|p|2 + |q|2)
The proof of (#) uses the f|AC|t that the square of the norm of any vector is equal to the inner product of that vector with itself: |v|2 = v⋅v. Also used is the distributive law for inner products. Then
|p + q|2 + |p − q|2 = (p + q)⋅(p + q)
+ (p − q)⋅(p − q)
=
p⋅p + 2p⋅q + q⋅q + p⋅p − 2p⋅q + q⋅q
=
|p|2 + |q|2 + |p|2 + |q|2
=
2(|p|2 + |q|2).
Now to show that [2.9b] is the vector interpretation of [2.9a].
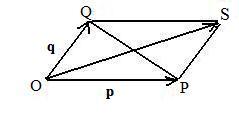
Construct the addition parallelogram OPRQ for finding the sum of position vectors p and q. (See adj|AC|ent figure.). The following equates non-negative scalar values:
(##)
OP = |p|, QO = |q|, OR = |p + q|, QP = |p − q||, PR = |q| and RQ = |p|
Since OPRQ is a parallelogram with diagonals QP and OR, the verbal part of [2.9a] justifies the equation
(###)
QP2 + OR2 = OP2 + PR2 + RQ2 + QO2
Repl|AC|e non-negative lengths QP, OR, OP, PR, RQ, QO by non-negative norms |p − q|, |p + q|, |p|, |q|, |p|, |q| respectively (see (##)) and collect like terms to obtain equation (#).
Two non-zero vectors locating points with array coordinates are perpendicular if and only if the dot product of those arrays is zero
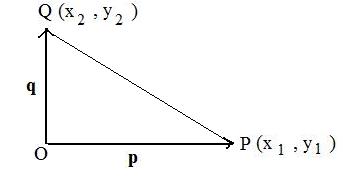 The proof is for arrays of size 2. There is a similar proof for arrays of size 3.
The proof is for arrays of size 2. There is a similar proof for arrays of size 3.
Let position vectors p,q locate points P(x1, y1) and Q(x2, y2). To prove that p,q are perpendicular if and only if p⋅q = x1x2 + x1x2 = 0.
The points P,O,Q form a triangle. Then p and q are perpendicular if and only if the triangle is a right triangle with the PQ as the hypotenuse.
From plane geometry, a triangle is a right triangle if and only if the square of the length of the longer side = sum of the squares of the lengths of the other two sides.This means that
(*) |PQ|2 = |OP|2 + |OQ|2
Then the squares of the lengths of the sides of this triangle are:
|p|2 = |OP|2 = x12 + y12,
|q|2 = |OQ|2 = x22 + y22,
|PQ|2 = (x1 − x2)2 + (y1 − y2)2 =
x12 − 2x1x2 + x22 + y12 − 2y1y2 + y22
Substituting the right sides of these equations into (*) produces:
x12 − 2x1x2 + x22 + y12 − 2y1y2 + y22 =
x12 + y12 +
x22 + y22
Simplifying,
x1x2 + y1y2 = 0
which is the dot product p⋅q = 0.
The steps can be reversed to prove "if and only if".
Vector product of parallel vectors
The vector product of two parallel position vectors is the zero vector.
Let p be any position vector, and let q be a parallel position vector. Then by definition of being parallel, q = λp for some real number λ.
Suppose p = (x,y,z). Then q = λ(x,y,z) = (λx, λy,λz). So the three 2x2 determinants for p x q become:
 |AC|cording to the diagonal \ product minus the diagonal / product rule the evaluations of these determinants are:
y λz − z λy = 0,
z λx − x λz = 0,
x λy − y λx = 0
Therefore p x q = (0,0,0) = 0.
|AC|cording to the diagonal \ product minus the diagonal / product rule the evaluations of these determinants are:
y λz − z λy = 0,
z λx − x λz = 0,
x λy − y λx = 0
Therefore p x q = (0,0,0) = 0.
Since PQ2 = PQ2, equating expressions in (3) and (4) produces:
(5) |p||q| cos θ = x1x2 + y1y2
If P(x1,y1,z1), Q(x2,y2,z2) are points in space, a similar derivation produces |p||q| cos θ = x1x2 + y1y2 + z1z2.
Proofs that the inner product of arrays satisfies the axioms for inner products
(a) The inner product of arrays is a real number (not an array): p⋅q = array1⋅array2 is a real number.
(b) The inner product of an array with itself is a non-negative real number: p⋅p = array1⋅array1 ≥ 0
(c) The inner product of an array with itself is zero if and only if the array is the zero array:
p⋅p = array1⋅array1 = 0 if and only if p = array1 = 0 (zero array)
(d) The inner product of arrays is commutative: p⋅q = array1⋅array2 = array2⋅array1 = q⋅p
(e) The inner product of arrays is distributive: p⋅(q + r) = array1⋅(array2 + array3) = array1⋅array2 + array1⋅array3 = p⋅q + p⋅r.
(f) A scalar may be factored out of the inner product: (λp)⋅q = (λarray1)⋅array2 = λ(array1⋅array2) = λ(p⋅q).
***
The proofs are for arrays of size 2. The proofs for arrays of size 3 are similar.
(a)
p⋅q = array1⋅array2 = x1y1 + x2y2 = sum of real numbers.
(b)
array1⋅array1 = (x1,y1)⋅(x1,y1) = x1x1 + y1y1
= (x1)2 + (y1)2
which is never negative, because it is a sum of squares of real numbers.
For this discussion consider position vectors u,v,w as locating points (x1,y1), (x2,y2), (x3,y3).
Evaluating left side: u⋅(v + w)
v+w = (x2 + x3, y2 + y3)
u⋅(v+w) = x1(x2 + x3) + y1(y2 + y3)
Evaluating right side: u⋅v + u⋅w
u⋅v = x1x2 + y1y2
u⋅w = x1x3 + y1y3
u⋅v + u⋅w = x1x2 + y1y2 + x1x3 + y1y3
Simple algebra shows that
x1(x2 + x3) + y1(y2 + y3) = x1x2 + y1y2 + x1x3 + y1y3
Therefore, u⋅(v + w) = u⋅v + u⋅w
Similar equations are true for position vectors in sp|AC|e where u,v,w locate points (x1,y1,z1), (x2,y2,z2), (x3,y3,z3).
Each of two non-zero position vectors is perpendicular to their vector product
Let p = (x1, y1, z1), and q = (x2, y2, z2) be triples.
It is advantageous to use the inline notation for vector product:
p x q =
(x1, y1, z1) x (x2, y2, z2) =
(y1z2 − z1y2,
z1x2 − x1z2,
x1y2 − y1x2)
To show that p is perpendicular to p x q it is sufficient to show that the inner product of p and p x q
(x1, y1, z1) ⋅ (y1z2 − z1y2,
z1x2 − x1z2,
x1y2 − y1x2)
is equal to the number 0. The inner product results in the left side of the identity
x1(y1z2 − z1y2) +
y1(z1x2 − x1z2) +
z1(x1y2 − y1x2) = 0
The reader can verify this identity with some algebraic computation.
A similar argument proves that q is perpendicular to p x q.
Area of a parallelogram
As given in analytic geometry the area of the parallelogram with vertices at
(0,0,0), (x1, y1, z1), (x2, y2,z2)
and (x1 + x2, y1 + y2, z1 + z2)
is equal to
sqrt(
(y1z2 − y2z1)2 +
(z1x2 − z2x1)2 +
(x1y2 − x2y1)2)
The formula for the area involves only triples, not considered as vectors here.
Right hand screw method for direction of vector product

The vector product of two position vectors is perpendicular to both vectors. There are ex|AC|tly two ways that position vector p x q can be perpendicular to this plane, and those ways are vectors pointing in opposite directions. The angle θ is measured from the first vector p mentioned in the vector product p x q to the second vector q in that same vector product. Always choose the angle that is between 0° and 180°.
Most screws are right-hand screws. This means that if the head of the screw is turned to the right, as indicated by the wavy red arrows in the two center figures, the screw will advance forward into the wood. Now pl|AC|e the screw at the origin O so that the f|AC|e of the head is in the plane of p,q . At the same time, the direction of θ be the same as the wavy red arrows on the head of the screw. Then p x q will point in the direction of the advancing screw when the head is turned (by a screwdriver). This direction is chosen, and not its opposite, so that vector products can be used in vector equations that more simply model some physical phenomena such as induction coils.
3x3 determinants and their evaluations
The evaluation of the determinant
 can be done by forming and adding products on diagonals \ \ \ as shown below, and then subtr|AC|ting products on diagonals / / / as shown below:
can be done by forming and adding products on diagonals \ \ \ as shown below, and then subtr|AC|ting products on diagonals / / / as shown below:

=
x1y2z3 +
y1z2x3 +
z1x2y3 −
z1y2x3 −
x1z2y3 −
y1x2z3
For example, to evaluate the determinant
 draw the diagonals and find the products along e|AC|h diagonal:
draw the diagonals and find the products along e|AC|h diagonal:

Switch the vector product and the inner product in a triple of vectors: p x q ⋅ r = p ⋅ q x r
Using simple algebra it is possible to show that the following three expressions E1, E2, E3 are equal (algebraic identities):
E1:
(y1z2 − z1y2) x3 +
(z1x2 − x1z2) y3 +
(x1y2 − y1x2) z3
E2:
x1 (y2z3 − z2y3) +
y1 (z2x3 − x2z3) +
z1 (x2y3 − y2x3)
E3:
x1y2z3 +
y1z2x3 +
z1x2y3 −
z1y2x3 −
x1z2y3 −
y1x2z3
One way is to multiply out the parentheses in E1 and E2 and show that e|AC|h of the two resulting expressions are equal to E3 by rearranging the terms. Therefore, expressions E1 and E2 are equal (identities).
If p = (x1, y1, z1),
q = (x2, y2, z2),
r = (x3, y3, z3),
then the expressions E1 and E2 are equivalent respectively to
E'1: p x q ⋅ r
E'2: p ⋅ q x r
Since expressions E1 and E2 are equal, then these two expressions are equal: p x q ⋅ r = p ⋅ q x r
The expression E3 is the same as the expression to evaluate a 3x3 determinant given |AB|ove. This means that if the triples of the three position vectors are known then the products p x q ⋅ r = p ⋅ q x r are equal to the (evaluation of) the determinant

A proof from plane geometry of the following theorem
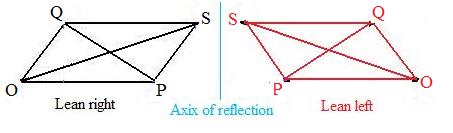
The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of the four sides.
Notation: In the adjacent figures:
(#) |PQ|2 + |OS|2 = |QO|2 + |OP|2 + |PS|2 + |SQ|2
|PQ|2 + |OS|2 = |QO|2 + |OP|2 + |PS|2 + |SQ|2
where the red figure is the mirror image of, and therefore congruent to, the black figure. Therefore red segments that correspond to black segments are congruent.segments. Any discussion about the black figure will have a corresponding discussion about the red figure: simply change the color of the words and symbols in the discussion from black to red. Therefore without loss of generality the following discussion will be in black, except for additional lines which are in blue.
Drop a perpendicular from Q to line OP meeting that line at M forming right triangles QMP and QMO. Then by the Pythagorean theorem
|PQ|2 = |QM|2 + |MP|2,
|QO|2 = |QM|2 + |OM|2
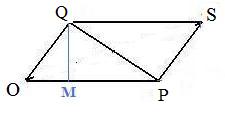 Eliminate |QM|2 from both equations to get
Eliminate |QM|2 from both equations to get
|PQ|2 = |QO|2 + |MP|2 − |OM|2
=
|QO|2 + (|OP| − |OM|)2 − |OM|2
=
|QO|2 + |OP|2 − 2 (|OP|)(|OM|) + |OM|2 − |OM|2
SO
(*) |PQ|2 = |QO|2 + |OP|2 − 2 (|OP|)(|OM|)
Drop a perpendicular from S to line OP meeting that line at N forming right triangles SNO and SNP. Then by the Pythagorean theorem
|OS|2 = |SN|2 + |ON|2,
|PS|2 = |SN|2 + |PN|2
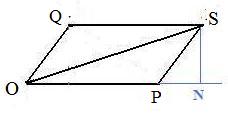 Eliminate |SN|2 from both equations to get
Eliminate |SN|2 from both equations to get
|OS|2 = |SP|2 + |ON|2 + |PN|2 =
|SP|2 + (|OP| +|PN|)2 − |PN|2 =
|SP|2 + |OP|2 + 2 (|OP|)(|PN|) + |PN|2 − |PN|2
So
(**)
|OS|2 = |OP|2 + |PS|2 + 2 (|OP|)(|PN|)
Therefore, adding equations (*) and (**) above:
|PQ|2 + |OS|2 = |QO|2 + |OP|2 − 2 (|OP|)(|OM|) + |OP|2 + |PS|2 + 2 (|OP|)(|PN|).
But right triangles QOM and SPN are congruent and therefore |PN| = |OM|. Therefore, the terms 2 (|OP|)(|OM|) and 2 (|OP|)(|PN|) subtract to get zero. Also |OP| = |SQ| because OPSQ is a parallelogram. Hence equation (#).
 Then cos θ ≥ 0.
Then cos θ ≥ 0. 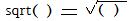
 Then cos θ ≤ 0. Hence (− cos θ) ≥ 0
Then cos θ ≤ 0. Hence (− cos θ) ≥ 0 The dot product was originally defined for arrays only. There is a geometric interpretation of this dot product that involves position vectors, their lengths and the angle between them. No arrays are involved in this interpretation.
Figure A shows a simple triangle OPQ. Figure B shows a congruent triangle with vectors p, q, QP as sides and arrays as coordinates:
The dot product was originally defined for arrays only. There is a geometric interpretation of this dot product that involves position vectors, their lengths and the angle between them. No arrays are involved in this interpretation.
Figure A shows a simple triangle OPQ. Figure B shows a congruent triangle with vectors p, q, QP as sides and arrays as coordinates: The adjacent figure shows the vector sum OS = p + q and how to get it, using the triangle method, from OP = p and PS = q. The shortest distance from O to S is along p + q. The distance |OP| + |PS| cannot be any shorter.
The adjacent figure shows the vector sum OS = p + q and how to get it, using the triangle method, from OP = p and PS = q. The shortest distance from O to S is along p + q. The distance |OP| + |PS| cannot be any shorter.
 The proof is for arrays of size 2. There is a similar proof for arrays of size 3.
The proof is for arrays of size 2. There is a similar proof for arrays of size 3.






 Eliminate |QM|2 from both equations to get
Eliminate |QM|2 from both equations to get Eliminate |SN|2 from both equations to get
Eliminate |SN|2 from both equations to get