Return to main page
Volume C Chapter 2
Exercises
Exercise 1.0
Does the system of odd natural numbers with the operation of multiplication form a group?
Exercise 2.0
Show that the additive collection 3J of multiples of 3 forms a group.
Exercise 3.0
Show that the integers mod 5 without zero = {1,2,3,4} is a multiplicative group. But the integers mod 6 without zero = {1,2,3,4,5} is not a multiplicative group.
Exercise 4.0 Symmetries of the Square
For the square there are four vertices that are on four immovable permanent points with location numbers 1, 2, 3, 4 as shown in the adjacent figures. Motions may pick up the square but always set it down so that its vertices are on the four points. Motions cannot twist or otherwise mutulate the square.
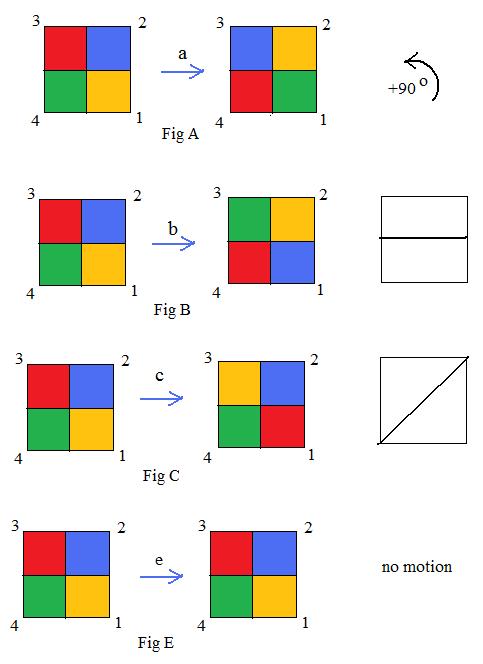
There are four basic motions:
(a) Pick up the square, rotate it about its center +90° counter-clockwise and put it down on the points. (Fig A)
(b) Pick up the square, flip it over about the horizontal line that bisects both vertical sides of the square (that were on points 2 and 3, and points 1 and 4). (Fig B)
(c) Pick up the square, flip it over about the diagonal that joins vertices that were on points 2 and 4 (Fig C).
(e) Pick up the square and put it down without any movement of rotation or flipping it about some line. Essentially, it is equivalent to no motion, leaving the square with vertices staying on the points. (Fig E)
The action e is that of an identity. e: 1 → 1, 2 → 2, 3 → 3, 4 → 4
(i) Find the arrow notations for motions: a, b, c, ab.
(ii) Using arrow notations, prove the following equalities: a4 = e, b2 = e, c2 = e, ac = b, ba = c, bc = a, ca = a2b, cb = a3.
The reader may assume the exponent laws hold: aa = a2, aaa = aa2 = a3, etc.
(iii) Using the equations in (ii) (and not arrow notations), prove: a2a3 = a abc = a2, ba2 = a2b, ba3 = ab.
