Figure A represents poles tied to boats.
All the ropes are elements of a relation from poles to boats. A relation may be thought of as directed links between elements in one set and elements in another set (although the two sets may be the same). There is no restriction on the links except that they relate elements in the two sets, and with nothing outside of them.
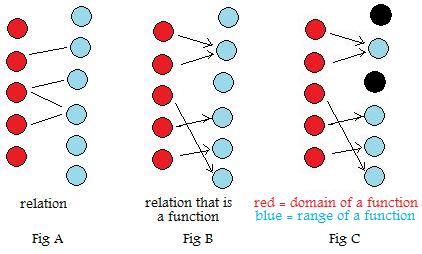
Fig B represents a different situation. Here five people want rooms in a motel with six rooms. The people go to their assigned rooms. (There is a married couple who are assigned the same room.) To indicate this, arrows are used to link elements in the first set with elements in the second set. Two conditions are satisfied by the relation in Fig B:
[1.1a] Every element in the first set is involved in the "arrow pointing." (Every guest is assigned a room. No guest is left without a room or assigned a room outside of this motel.)
[1.1b] No arrow points from any single element in the first set to two or more different elements in the second set. (No guest is assigned to two or more rooms.)
The relation in Fig A fails both of these conditions.
In Fig C, which shows the same relation as Fig B, the elements having no arrow pointing at them are made black. (The two unassigned rooms remain in darkness.) The remaining blue elements are called images of elements in the first set. (Each image is an occupied room with one or more guests assigned to it.
[1.1c]
A function from (all of) a first set to a second set is a
is a relation between the sets, with the conditions that the relation involves each element in the first set once and only once and that one or more elements of the second set are involved.
[1.1d] To each element in a set U a function f from U to a set V relates each element u in U to an element f(u) in V.
Because arrows are sometimes used to show the action, it is said that a function carries an element u onto an element f(u), which is the image of u.
If the elements in Fig C are replaced respectively by the integers in P5 and P6 the actions of the function on each element can be written in an arrow notation:
If the function is given the name f then the notation f: P5 --> P6 tells from where f is getting the elements and to where f is carrying them. Also the notation
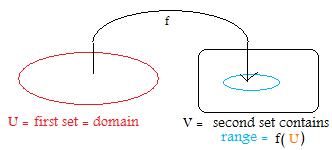
In general, the notation f: U --> V means that f carries each element in U onto elements (images) in V. The first set U is called the domain of f. The collection of images, which is really a subset of V, is called the range of f. The range of f is often denoted by f(U) where U is the domain of f.
Recall that in section 2 of the previous chapter 3 ordered pairs (u,v) were used to relate elements of the first set U to elements of the second set V. This notation can be used to define a function:
[1.1e] A function from a first set to a second set is a collection of ordered pairs in which all of the elements of the first set appear once and only once as first coordinates. Only elements from the second set may appear as second coordinates.
In the previous example, domain of f is all of P5 and the range of f is {2,4,5,6}. Using the colors shown in Fig C, the second set P6 might be written (with 1 and 3 in black) as {1,2,3,4,5,6} to show the range of f as part of P6. In general, in these discussions elements in the second set, yet are not in the range (they are not images), are sometimes written in black in discussions in this volume to increase clarity. If the range is not determined the second set is written in black color.
There are tables of numbers included in the back of some textbooks. In one book on solid geometry there is a table of square roots. It associates with each integer from 1 to 200 its real square root. By giving this list, the table serves as a function from P200 to the set of (non-negative) real numbers. Another table associates with each integer from 0 to 90 (in degrees) a real number between 0 and 1 inclusively. It is a (limited) table of the trigonometric function called sine. The image of 0° is 0, the image of 30° is 1/2 and the image of 90° is 1. More detailed tables can give the values of sine between integers as well. There are also tables of logarithms. However, the domain of the log function is the set of positive real numbers. The log function always carries 1 onto 0.
It is quite useful to allow the domain of a function to consist of ordered pairs. Suppose that the domain of a function f to be the set:
For example, f(k) = 2k defines a function f: P --> P. An attempt to list the elements in P might be {1,2,3,4,5,6,7,8,....}. The range is the set of all even positive integers = {2,4,6,8,...}. This last set might be denoted by the symbol 2P.
g(x) = x2 defines a function g: R --> R. The range is the set of all non-negative real numbers, because squares of real numbers are never negative.
The functions f and g have been given by formulas. Now f carries the positive integer 5 onto the positive integer 10 and g carries the real number -1.2 onto the real number 1.44. The notation f(5) = 10 and g(-1.2) = 1.44 indicates these actions by f and g. The variables k and x used to help define these functions are called dummy variables. They can be replaced by other symbols. For eample f(a) = 2a and g(b) = b2. In fact, f(u + v) = 2(u +v) = 2u + 2v and g(x - 2y) = x2 - 4xy + 4y2.
[1.2] The rule here is: if the variable inside the parenthesis after the function symbol is replaced by any expression, then every occurrence of that variable is replaced by the same expression..
Sometimes it is necessary to see if an element y in the second set is in the range of some function f (then it becomes a blue y). If f(x) = an expression involving x, then replace f(x) by y = that expression, and try to solve for x.
For example, if f: R --> R is defined by f(x) = x2, then 9 is in the range of f because 9= x2 can be solved for x, namely 3 and -3. However, -16 is not in the range of f because -16 = x2 cannot be solved using real numbers (imaginary numbers are not allowed here, because the domain was defined as the set of real numbers). The square of any real number x is never negative.
Similarly, if g: P --> P is defined by g(n) = 2n, the integer 6 is in the range of g because 6 = 2n can be solved for n, namely n=3. However, 7 is not in the range of g because 7 = 2n cannot be solved for n using only positive integers (fractions are needed here).
These two examples show that the definition of the function and what is in its domain determine what is in the range.
An important tool of mathematics is the infinite sequence. They can be in any set. Consider the sequence
[1.3] An infinite sequence in a set V are all the images of the set P of positive integers under some (sequence) function from P to V.
Some functions measure the sizes of subsets. For example, for finite subsets, f(S) = number of elements in the subset S. There are size functions in geometry. Functions L1 may give the lengths of line segments, L2 may give the areas inside a closed curves, L3 may give the volume of a solid. Such functions show the usefulness of functions whose domains are collections of sets.
It happens that the function f given in (*) above can also be defined by means of a formula: f(x,y) = x + 2y.
There is an infinite supply of functions. It is sometimes necessary to know when they are the same.
[1.4a] Two functions are equal if and only if they have identical truth sets of ordered pairs.
This definition is accurate, but may not be as intuitive as the following:
[1.4b] Two functions f and g from a common first set to a second set are equal if, for every element x, the images f(x) and g(x) are the same.
This definition [1.4b] says that two functions from the same set are equal if they do the same thing to each element in the domain. f = g if and only if f(x) = g(x) for every x in the domain.
If f and g are functions from R to R, defined as
The definition [1.4a] says that as x runs through all elements of the first set, the ordered pairs (x,f(x)) and (x,g(x)) are equal. In the arrow notation ([1.4b]), for each element in the domain the pair of arrows under f and under g point to the same image. If the two functions are functions from R to R, and they can be graphed in the coordinate plane of elementary algebra, then their curves coincide.