Examples of Important Functions
The Characteristic Function φ
By definition every logical statement is either true or false. Let these truth values be denoted by 1 and 0 respectively.
If p is a logical statement, then define φ(p) = 1 if p is true, and φ(p) = 0 if p is false. Here φ is a function from the set of a all logical statements into the set {0,1}.
For example φ(Germany is in Europe) = 1 and φ(All triangles have 4 sides) = 0.
return to chapter 4 on Functions
Functions Whose Domains Are Collections of Ordered Pairs
The product
P3 x P2 = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)}
Let π1 be the function that carries each ordered pair onto its first coordinate:
π1(1,1) = 1,
π1(1,2) = 1,
π1(2,1) = 2,
π1(2,2) = 2,
π1(3,1) = 3,
π1(3,2) = 3
Similarly let π2 be the function that carries each ordered pair onto its second coordinate:
π2(1,1) = 1,
π2(1,2) = 2,
π2(2,1) = 1,
π2(2,2) = 2,
π2(3,1) = 1,
π2(3,2) = 2
The functions
π1: P3 x P2 --> P3
and
π2: P3 x P2 --> P2
are known as projections.
- - - - - - - - - - - - - - - - - - -
The following is a definition.
Ordered pairs are the elements of the product UxV of any two non-empty sets U and V (U and V may be the same set). The functions
π1: UxV --> U
and
π2: UxV --> V
defined by
π1(u,v) = u
and
π2(u,v) = v
are called in these discussions respectively
projection of the product (back) onto the first set
and
projection of the product (back) onto the second set
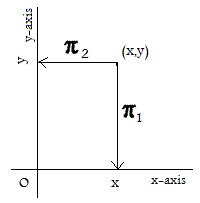
The term "projections" is motivated by the projections of the coordinate plane of elementary algebra onto the x-axis and y-axis. The functions π1(x,y) = x and π2(x,y) = y carry the point (x,y) perpendicularly onto x on the x-axis and onto y on the y-axis, respectively. See the adjacent figure. (Actually, the points x and y on the axes are identified with points (x,0) and (0,y) in the coordinate plane.)
- - - - - - - - - - - - - - - - - - -
The operation of addition x + y of real numbers is well known. However, it is actually a function from a set of ordered pairs. Writing it as +(x,y) emphasizes this fact, but is never written this way. Addition, subtraction and multiplication are functions from RxR --> R. They simply add, subtract and multiply the coordinates of any ordered pair in RxR. Division by zero is not allowed, so division is a function from RxQ --> R, where Q = set of real numbers R with zero removed. These functions are called binary operations of arithmetic. In any rigorous development of the familiar number systems, these operations are defined precisely in the language of functions.
Integers mod n
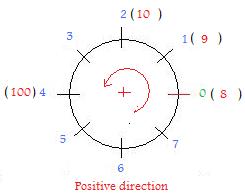 In order to discuss another function it is necessary to build up a set that will be the image of the set J of all integers. On a circular race track, 8 markers (sign posts) are placed at equal intervals. The starting point has marker 0. The remaining posts are markers 1,2,3,4,5,6,7. There is no marker 8. That place is occupied by marker 0. Likewise, there is no marker 9, that place is occupied by marker 1. Instead of 10 there is 2, etc.
In order to discuss another function it is necessary to build up a set that will be the image of the set J of all integers. On a circular race track, 8 markers (sign posts) are placed at equal intervals. The starting point has marker 0. The remaining posts are markers 1,2,3,4,5,6,7. There is no marker 8. That place is occupied by marker 0. Likewise, there is no marker 9, that place is occupied by marker 1. Instead of 10 there is 2, etc.
A revolution is a complete turn around the race track. A person or car must go from marker 0 around the circle through markers 1,2,3,4,5,6,7 once and back to marker 0. Notice that the place for marker 10 is already occupied by marker 2 because 10 = 1 rev + 2. Since 8 = 1 rev + 0, the starting place is already occupied by marker 0. Denote the set of existing markers by J8 = {0,1,2,3,4,5,6,7}. To find what marker in J8 already occupies the place where marker 100 should go, divide 100 by 8 to get the number of revolutions and look at the remainder: 100 = 12 rev + 4. The remainder 4 is the answer.
For any positive integer k, k = (number of rev) + (remainder) where the remainder is one of the integers in J8. Arithmetically this is written k = (number of rev)*8 + (remainder). The integral quotient k divided by 8 is the (number of rev). The (remainder) is the number in J8:
8 -> 0, 9 -> 1, 10 -> 2, ..., 101 -> 5, ...
 This is the beginning of constructing a function from the set of integers J onto J8. To complete the construction, the images of the negative integers must be determined. A negative revolution is one trip around the race track from marker 0 to marker 0 but in the opposite direction, that is, through 7,6,5,4,3,2,1 in that order. Then
This is the beginning of constructing a function from the set of integers J onto J8. To complete the construction, the images of the negative integers must be determined. A negative revolution is one trip around the race track from marker 0 to marker 0 but in the opposite direction, that is, through 7,6,5,4,3,2,1 in that order. Then
-0 = -1 rev + 0,
-1 = -1 rev + 7,
-2 = -1 rev + 6,
-3 = -1 rev + 5,
-4 = -1 rev + 4,
-5 = -1 rev + 3,
-6 = -1 rev + 2,
-7 = -1 rev + 1,
Using the notation of a function:
[*]
-0 --> 0,
-1 --> 7,
-2 --> 6,
-3 --> 5,
-4 --> 4,
-5 --> 3,
-6 --> 2,
-7 --> 1,
Table [*] can be used to find the image of any negative integer. For example,
(11 --> 3)
-11 --> -3 --> 5,
(24 --> 0)
-24 --> -0 --> 0,
(25 --> 1)
-25 --> -1 --> 7,
(101 --> 5)
-101 --> -5 --> 3
Notice that if 8 is added to the negative integers in table [*] then their equivalents in J8 appear.
A generalization of the 8 markers can be made: at equal intervals around the circle place n markers at equal intervals, where n is a positive integer. This will involve integers in the set Jn = {0, 1, 2, ..., n-1}. The function from J onto Jn
if k>=0, k --> remainder after dividing n by k,
if k<0, find the remainder after dividing n by -k and then subtract that remainder from n.
Replacing 12 by 0, then J12 = {0,1,2,3,4,5,6,7,8,9,10,11} are hourly markers on a circular face of a clock. Then
15 --> 3,
72 --> 0,
-15 --> -3
--> 9 (= 12 - 3)
J24 represents the hourly markers on a 24 hour clock, and is better to convert any number of revolutions into days and with any remainder as time on this clock 89 --> 17 (5 pm) (plus 3 days).
Another example is J360. It represents the integral degrees in one revolution about a circle.
1000 degrees --> 280 degrees (plus 2 revolutions).
-1000 degrees --> -280 degrees --> 80 degrees (360 - 280).
==========
Another example is used oftn in advanced mathematics as a counter-example. The R1 = reals mod 1 are all the real numbers from zero to one, including 0 but not including 1. The numbers 0.7, 0.2456, π/4, 0 are in R1.
But 1, 4.7, -0.000000001, π are not in R1.
To define the function from the real numbers R onto R1, let x be any positive real number in the form of a decimal. Delete the part before the decimal. The remainder (the decimal point and the part after it) is in R1.
5.3829 --> .3829.
11/4 = 2.75 --> .75.
-.345 --> .655 (= 1 - .345).
Recall that a proper subset is any subset, but not the whole set.
There is no one-to-one correspondence between Pn and any proper subset.
Let q(n) denote the above statement. A rigorous proof is by induction:
(a) q(1) is true;
(b) show that q(n) ==> q(n+1).
A more intuitive proof is given here. Reversing its steps suggests the proof by induction. (See Chapter 1, section 8 of this volume)
Suppose there are n balls to be put into fewer cans. An attempt is made to put exactly one ball in each can. The argument here will show that no matter the value of n (but n must be a positive integer) the attempt will fail:
Let r(n) be the open statement
r(n): it is impossible to put n balls into fewer cans, no can is to contain more than one ball.
In the case of r(1), there are no cans, so r(1) is trivially true.
For r(2) there is at most 1 can. Take away the can and one ball, and the situation becomes that of r(1) which is true.
for r(3) there are at most 2 cans, and more balls. Take away a can and one ball and the situation becomes that of r(2), which is true.
This process continues, the truth of r(n-1) implies the truth of r(n).
q(1) is true because P1 = {1} has only one proper subset, namely the empty set. With no elements in it, the empty set cannot be in one-to-one correspondence with any non-empty set.
Another very different notation is often used. For a simpler introduction to it a different permutation is used:
1 2 3 4 5 6
5 6 1 2 4 3
Suppose there is a single guest in each of 6 rooms of a motel. The persons are reassigned to the rooms by the following method: if a person moves to a different room and tells that occupant go to another room. It all starts with the person in room 1 who is told by the manager to go to room 5
That person goes to room 5 and tells the occupant to go to room 4 .
That person goes to room 4 and tells the occupant to go to room 2 .
That person goes to room 2 and tells the occupant to go to room 6 .
That person goes to room 6 and tells the occupant to go to room 3 .
That person goes to room 3 and tells the occupant to go to room 1 .
These actions can be accurately denoted by the
[5.5] cyclic arrow notation:
1 --> 5 --> 4 --> 2 --> 6 --> 3 --> 1
The manager could have started this chain reaction with the person in room 4 and accomplished the same reassignment:
4 --> 2 --> 6 --> 3 --> 1 --> 5 --> 4
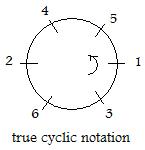 Notice that in this cyclic notation, the first and last numbers are the same, but no other number appears twice. For this reassignment (permutation) every person gets "bumped" to a new location.
Notice that in this cyclic notation, the first and last numbers are the same, but no other number appears twice. For this reassignment (permutation) every person gets "bumped" to a new location.
The word "cyclic" implies that a circular motion is involved. The adjacent figure shows this permutation byplacing the numbers in [5.5] around a circle in a counter-clockwise direction (the arrow inside the circle shows this direction). A (horizontal) cyclic notation for the same permutation can begin with any number, go counter-clockwise and return to that starting number.
The two (horizontal) notations given above omit the arrows, include every number once and only once, and include everything in parentheses:
[5.6] cyclic notations of a permutation
(1 5 4 2 6 3) and (4 2 6 3 1 5)
It is understood that the first number in the cyclic notation can be attached after the last number to give the arrow notation.
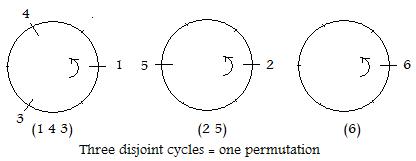 Consider now the permutation:
Consider now the permutation:
1 2 3 4 5 6
4 5 1 3 2 6
The cyclic arrow notation for this permutation is:
1 --> 4 -- >3 -->1,
2 -->5 -->2, 6 --> 6
and the cyclic notation is:
(1 4 3)(2 5)(6)
This requires two non-trivial circles:
The cycle of one number (6) may be omitted. Missing cycles of one element indicate that element is a fixed point. However with (6) as part of the notation, the true length of the permutation can be seen. For example, (1)(2)(3)(4)(5)(6)(7) denotes the identity transformation on P7. All the elements are fixed points.
Symmetries of the Equilateral Triangle
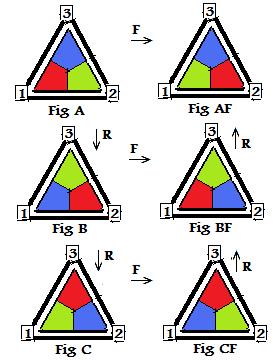 Figure A is the starting place, the first view of the colored triangle inside the black frame. Going down the left column of figures, rotate the colored triangle in Fig A 120° counter-clockwise to get Fig B. Rotate the colored triangle in Fig B 120° counter-clockwise to get Fig C. The rotations are indicated by the arrow pointing down and with the label R.
Figure A is the starting place, the first view of the colored triangle inside the black frame. Going down the left column of figures, rotate the colored triangle in Fig A 120° counter-clockwise to get Fig B. Rotate the colored triangle in Fig B 120° counter-clockwise to get Fig C. The rotations are indicated by the arrow pointing down and with the label R.
Imagine a vertical line through 3. (On it is an altitude of the triangle. ) Reflect the triangle about this line (axis) to go from any figure in the left colume to the corresponding figure in the right column. For example, a reflection about this vertical line changes Fig A into Fig AF. Similarly for B,BF and C,CF. The reflection is indicated by the double arrow <--> and the letter F.
To get the actual permutation F from the physical reflection F about the vertical axis of each triangle (going from figures in the left column to figures in the right column), notice that the top vertex at 3 is always a fixed point. That colored angle stays fixed pointing at 3. But a change happens. Therefore the angles at 1 and 2 much be swapped. The permutation must be:
F
1 -- > 2
2 -- > 1
3 --> 3
The physical rotation R of any triangle is about the center located where the three colors come together. The counter-clockwise direction is considered positive. Then R moves any triangle through an angle of +120°. Therefore Fig B shows the result of the rotation of the colored triangle in Fig A. Examining how the red, green, blue angles have moved leads to the following permutation:
R
1 --> 2
2 --> 3
3 -- > 1
The rotation R through +120° also rotates the colored triangle in Fig B onto the colored triangle in Fig C. Notice that this same rotation carries the colored triangle in Fig CF onto the colored triangle in Fig BF, and in turn BF onto AF, but in the reverse direction (bottom to top) than what R did in the left column (top to bottom).
Using rotations and the reflection about the vertical axis, it is possible to go from the colored triangle in Fig A to the colored triangle in any figure, including A itself using the identity transformation.
Similarly R moves the colored triangle in Fig B onto the colored triangle in Fig C.

 In order to discuss another function it is necessary to build up a set that will be the image of the set J of all integers. On a circular race track, 8 markers (sign posts) are placed at equal intervals. The starting point has marker 0. The remaining posts are markers 1,2,3,4,5,6,7. There is no marker 8. That place is occupied by marker 0. Likewise, there is no marker 9, that place is occupied by marker 1. Instead of 10 there is 2, etc.
In order to discuss another function it is necessary to build up a set that will be the image of the set J of all integers. On a circular race track, 8 markers (sign posts) are placed at equal intervals. The starting point has marker 0. The remaining posts are markers 1,2,3,4,5,6,7. There is no marker 8. That place is occupied by marker 0. Likewise, there is no marker 9, that place is occupied by marker 1. Instead of 10 there is 2, etc.
 This is the beginning of constructing a function from the set of integers J onto J8. To complete the construction, the images of the negative integers must be determined. A negative revolution is one trip around the race track from marker 0 to marker 0 but in the opposite direction, that is, through 7,6,5,4,3,2,1 in that order. Then
This is the beginning of constructing a function from the set of integers J onto J8. To complete the construction, the images of the negative integers must be determined. A negative revolution is one trip around the race track from marker 0 to marker 0 but in the opposite direction, that is, through 7,6,5,4,3,2,1 in that order. Then
 Notice that in this cyclic notation, the first and last numbers are the same, but no other number appears twice. For this reassignment (permutation) every person gets "bumped" to a new location.
Notice that in this cyclic notation, the first and last numbers are the same, but no other number appears twice. For this reassignment (permutation) every person gets "bumped" to a new location.
 Consider now the permutation:
Consider now the permutation:
 Figure A is the starting place, the first view of the colored triangle inside the black frame. Going down the left column of figures, rotate the colored triangle in Fig A 120° counter-clockwise to get Fig B. Rotate the colored triangle in Fig B 120° counter-clockwise to get Fig C. The rotations are indicated by the arrow pointing down and with the label R.
Figure A is the starting place, the first view of the colored triangle inside the black frame. Going down the left column of figures, rotate the colored triangle in Fig A 120° counter-clockwise to get Fig B. Rotate the colored triangle in Fig B 120° counter-clockwise to get Fig C. The rotations are indicated by the arrow pointing down and with the label R.