P that are not images, for example, 3,4,6,7,8,9,11,..... To show that 7 is not an image, try to solve x2 + 1 = 7 for x. This is impossible because the square roots of 6 are not integers. This means that 7 is outside the range of f (See [3.1b] above.) Therefore the function f is not onto the set P. However the function is into (as well as to) the set.
For more examples and discussions of functions that are onto and functions that are not onto but merely into, click here.
It should be noticed that a function is always into the second set (because all the images are there), but not always onto the second set (there may be some elements that are not images). Being into does not exclude being onto. Perhaps the word "to" should replace the word "into" to remove any confusion about being "into."
There is a natural carryover to the working definition of a function. It is suggested by [1.2b]. Suppose there is a function from a first set onto a second set. Then each element y in the second set is the image of one or more elements x. All these different x's form a collection of subset of the first set. Let y run through all the elements in the second set, producing subsets of first set.
It would not be difficult to show directly that these subsets form a partition of the first set. But this can also be done by using some equivalence relation. Two elements are related iff they have the same image under the function. It is easily verified that this relation is an equivalence relation. The subsets form a partition of the first set. Click here for more discussion of this topic.
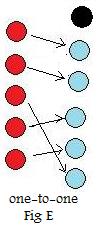
Make a slight adjustment in Fig. C to get the adjacent figure Fig E. In Fig C two arrows point to the same blue element. The second arrow is changed to point to a different element, changing its color from black to blue. In Fig E all arrows point to different (blue) elements.
(Notice that the functions in Fig C and in Fig E are not "onto.")
[3.3a]
A function from a first set into a second set is one-to-one if all the images are distinct.
[3.3b]
A function f from a first set into a second set is one-to-one if for any distinct elements (in the first set) their images (in the second set) are distinct.
This definition can be stated in terms of elements: f is one-to-one iff the following implication is always true:
x1 not equal to x2 ==> f(x1) is not equal to f(x2)
[3.3c]
A function from a first set into a second set is one-to-one if the following implication is always true:
f(x1) = f(x2)
=>
x1 = x2
for any x1,x2 in the first set.
Actually, the implication in [3.3b] is the contrapositive of the implication in [3.3c].
The following function from P4 into the second set {A,B,C,D,E,F,G} is one-to-one:
1 ----------->D
2 ----------->G
3 ----------->B
4 ----------->C
None of the arrows point to the same letter. Arrows from different numbers point to different letters. Definitions [3.3a] and [3.3b] are convenient to use to see if functions with small domains are one-to-one or not.
For functions defined by algebraic formulas or equations definition [3.4c] is often more useful. The function f from the set P of all positive integers into itself (P --> P) defined by f(x) = 2x is also one-to-one. To prove this, a chain of implications supports the implication in definition [3.3c]:
f(x1) = f(x2) ==> 2x1 = 2x2
==> x1 = x2 (division of both sides by 2)
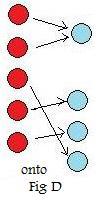
The last two examples show functions that are one-to-one but not onto the second set. (Click here to see why sometimes these functions are called injections.) Fig D amd [3.2] show a function that is onto but not one-to-one. Fig E shows a function that is one-to-one but not "onto". A question remains: are there functions that are both onto and one-to-one? The answer is yes. They are the one-to-one correspondences.
Before leaving this section on one-to-one functions and functions that are "onto", the products of such functions should be examined. Recall that a function g is conformable with a function f if the product gf can be formed (i.e. domain of g is contained in the range of f).
[3.4] Theorem
If two functions f and g are both "onto" (and g is conformable with f), then their product gf is "onto".
Let set V be the domain of g.
Let f: U ---> V and g: V ---> W be "onto" functions. Let w be any element in W. Since g is onto (all of) W, w is an image, and this means that for some v in V, g(v) = w. Since f is onto (all of) V, v is an image, and this means that for some u in U, f(u) = v. Apply g to both sides of this last equation: gf(u) = g(v) = w. So w is an image under gf. This means that all elements of W are (indirectly) images of elements in U. Therefore, the product gf: U ---> W is "onto."
Click here to see examples of products of functions that are "onto."
[3.5] Theorem
If two functions f and g are both one-to-one (and g is conformable with f), then their product gf is one-to-one.
Let set V be the domain of g.
Let f: U ---> V and g: V ---> W be one-to-one functions. Let u1 and u2 be any distinct elements of U. Since f is one-to-one, f(u1) and f(u2) are distinct elements in V. Since g is one-to-one, gf(u1) and gf(u2) are distinct elements in W. Therefore, gf carries distinct elements in U onto distinct elements in W. So gf is one-to-one.
Click here to see examples of products of functions that are one-to-one.
[3.6]
A function is a one-to-one correspondence if and only if the function is both one-to-one and "onto."
If f is a one-to-one correspondence from a set U to a set V then every element in V is involved once and only once. Since every element in V is involved, every element in V is an image. Therefore, the range of f is all of V. Hence f is "onto." Also f is one-to-one because no element in V is involved more than once.
Reversing the steps and modifying some of them show that a one-to-one function that is "onto" is a one-to-one correspondence.
The statement [3.6] provides a method to show that some function is actually a one-to-one correspondence.
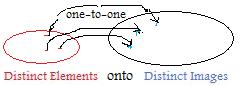
 In the previous section it was said that the range of a function from a first set into a second set is contained in that second set because it is a subset. The word into makes no restriction on the size of the range. (But it cannot be empty because there would be no function.) Therefore, it may happen that the range is all of the second set. Abstractly, the situation is shown in the adjacent figure. All the elements in the second set are images. Intuitively speaking, this means that every element in the second set is on the "receiving end" of the function's arrows, and the second set can be written in blue, instead of black.
In the previous section it was said that the range of a function from a first set into a second set is contained in that second set because it is a subset. The word into makes no restriction on the size of the range. (But it cannot be empty because there would be no function.) Therefore, it may happen that the range is all of the second set. Abstractly, the situation is shown in the adjacent figure. All the elements in the second set are images. Intuitively speaking, this means that every element in the second set is on the "receiving end" of the function's arrows, and the second set can be written in blue, instead of black.

