The clerk who assigns the rooms needs a system that tells what rooms have been assigned and what rooms are free (not assigned). The room numbers become blue if the rooms have been assigned. Otherwise, numbers remain black for unoccupied rooms. After the above people have been assigned rooms as shown, the lights show
Consider a different relation that associates each integer with its square. Consider another relation that associates each integer with another integer that is three greater. One way of expressing these relations uses equations y = x2 and y = x + 3. This gives y two different meanings. Instead of an ambiguity for y, give the relations different names, say f and g. Then f squares integers, and g adds three to them. Let f(x) and g(x) denote the images of these actions on any integer x. Therefore,
[1.1a]
A function from a first set to a second set is a collection of ordered pairs in which all of the elements of the first set appear once and only once as first coordinates.
[1.1b] To each element in a set U a function f from U to a set V relates each element u in U to an element f(u) in V. The function f is from all of U.
Sometimes, f is said to carry an element u onto an element f(u) in V. That element f(u) is called the image of the element u in U. In the example above of persons in a motel, each of the room numbers in blue in the motel M is an image of a person or persons in crowd C occupying that room. The numbers of unoccupied rooms are not images because no person has been assigned to them.
The symbol f: U --->V means that f is a function from a set U to a set V. This notation replaces the tilde notation U ~ V. The arrow notation is extended to elements, u ---> v, where v = f(u); (Click here to see this notation used with the example above of people staying in the motel.) This means that u ---> f(u). and (u,f(u)) is an ordered pair in the relation-set of f.
It is quite possible that the first set U and the second set V are the same. In that case the notation f: U --->U can be used. This often happens with sets of numbers:
f: P ---> P, g: J ---> J h:R ---> R where P,J,R are the sets of positive integers, integers, real numbers respectively. When real numbers or some sets not labeled U,V,W, it is customary to use the letters x,y,z as elements, replacing u,v,w.
In the adjacent figure a curve y = f(x) of a function fhas been plotted in the usual way. For each value of x a value for y = f(x) has been calculated, and the point (x,f(x)) is plotted in the coordinate plane. Theoretically f is an infinitely long curve (in both directions) but only a portion is drawn here. Notice that in plotting the points the first coordinate and the second coordinate are found which make up the relation-set of f. Constructing graphically relation-sets of functions in elementary algebra is what plotting those curves is all about!
However, for a function, no part of its curve can be above or below itself, it cannot curve back there. Otherwise, that would give two values for f(x).
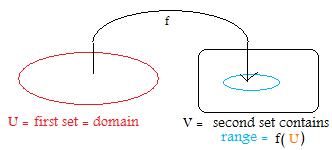A function f: U ---> V is completely determined by its ordered pairs (u,f(u)) where all first coordinates u are taken from the first set, and all second coordinates f(u) are taken from the second set mentioned in [1.1a]. All those first coordinates u form a set called the domain of the function. The domain is always the entire first set(otherwise, the function is not from the first set, but from a proper subset). All those second coordinates f(u) form a subset (of images) of the second set called the range of the function. The range of f is often denoted by f(U). In these discussions the domain is often indiced by a red color, and the range by a blue color. A set containing the range has a black color.
The domain of the function, that assigns the 12 people to rooms, is that same set C of people. The range is the set of assigned rooms, namely, { 1,3,4,5,7 }. For the function f that squares integers, the domain J is the set of all integers. But the range f(J) is the set of zero and the positive integers because squaring cannot produce a negative integer. For g the domain J and the range J are equal, namely, the set of all integers.
One way to see if an element y is in the range of a function h: J ---> J or h: R ---> R is to form an equation y = h(x) and try to solve for x. For example, 9 is in the range of the squaring function f because the equation 9 = x2 can be solved for x. However, -25 is not in the range of f because the equation -25 = x2 cannot be solved using integers. 5 is another integer not in the range of f Every integer is in the range of g because in the equation y = x + 3, it is possible to solve for x (x = y - 3).
[1.2] Every function naturally partitions its domain into (disjoint) subsets. For each image in the second set, form a subset of all elements in the domain that are carried onto that image. For example, all the people occupying room 1 form a subset {Jim, Jack, Joe, Jude}. The partition of the entire crowd C is the collection of subsets:
[1.3a] Two functions f and g from a first set to a second set are equal if, for every element x in the first set, the elements f(x) and g(x) in the second set are equal.
[1.3b] Two functions are equal if and only if they have identical relation-sets.
Both [1.3a] and [1.3b] say that as x runs through all elements of the first set, the ordered pairs (x,f(x)) and (x,g(x) are equal. In the arrow notation, for each element in the domain the pair of arrows under f and under g point to the same image. If the two functions are functions from the real numbers R to the real numbers R, so they can be graphed, then their curves coincide.
Equal functions have the same domain and the same range. Two functions with different domains cannot be equal. In the accommodation of people and motel rooms given above, if some of the people are evicted from their motel rooms, then a new assignment function has been created. It has a smaller domain than the crowd C of all 12 people. After the eviction the set of ordered pairs in the relation-set is reduced in size, and the new function of room assignments is different from the old function.