program to generate permutations in lexicological order
program to generate permutations in alternating odd-even order

Section 5  Permutations

A set is finite if all the elements can be counted and the counting stops with some positive integer n. In this discussion an array is a finite collection of distinct objects arranged in a row.

Many people think of a permutation of (distinct) objects as a rearrangement of those objects in some array. Intuitively speaking, a permutation somehow picks them up from some array, mixes them and places them back in that array.

Example 1: Some permutation has picked up the array '1 2 3 4 5' and put down the array '4 5 3 1 2' in its place. Intuitively speaking, a permutation has "mixed up" the five numbers 1,2,3,4,5 that were in numerical order.

Example 2: Some permutation has picked up the array 'a b c d e' and put down the array 'd e c a b' in its place. Intuitively speaking, a permutation has "mixed up" the five letters a,b,c,d,e that were in alphabetical order.

Recall that a set is determined by its elements, and they can be listed in any order. For example, P5 = {1,2,3,4,5} = {4,5,3,1,2} = {5,4,3,2,1}. The elements in P5 can be listed as 1,2,3,4,5 and any other order of the listing will do. It is the content of the set that is important, not in what order they are listed. But array '1 2 3 4 5' is not equal to array '4 5 3 1 2' because the order of the numbers is different. In these discussions, using commas shows order is not important; using spaces between elements and ' ' before and after the array (usually in dark print) shows order is important: '4 7 2 1 6 5 3' is not equal to '6 2 5 1 3 7 4', but their contents can be listed as {1,2,3,4,5,6,7}.

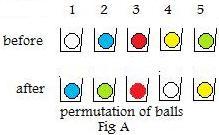Example 3: The adjacent figure, Fig A, shows two rows of five balls of different colors in five containers. A permutation rearranges them by picking them up out of the containers and puts them back in the same containers, but in a different order, shown in the bottom row of the same figure.

In Fig A, the bottom row is a permutation of the balls in the top row. Unlike the example of letters, there is no natural order of the balls in the top row to be "mixed up" by some permutation.

From these examples comes a simple, intuitive description of a "physical" permutation:
[5.1] A "physical" permutation picks up all the objects in a finite array, and puts them back, usually in a different order.

Notice that the objects, after the permutation has acted, are the same as the objects before the action. No objects are lost, no new objects are added.

Since the objects are in an array (row) there is an object in the first place, another object in the second place,... and an object in the last place. (There is a last place because the array is finite.) In example 2, before the permutation acts, a is in first place, b in second place, ..., and e is in last place. All this can be displayed as follows:

1   2   3   4   5
a   b   c   d   e
After the permutation has acted, d is in first place, e is in second place,..., and b is in last place. This result can be represented as follows:
1   2   3   4   5
d   e   c   a   b
(When the two rows appear as together in one table, the marks ' ' will usually be omitted.) These tables of two rows show locations and the objects in those locations. Comparing the tables, it is seen that the permutation "carries" the letter a from location 1 to location 4, b from 2 to 5, c from 3 to 3, d from 4 to 2, and e from 5 to 2. This action can be written in the following notation:
[5.2]
1 --> 4      1 --> 4
2 --> 5      2 --> 5
3 --> 3      3 --> 3
4 --> 1      4 --> 1
5 --> 2      5 --> 2
This reveals the "scheme" of the permutation. It shows the action of the permutation on each letter.

An examination of example 3 shows the same permutation has acted. To show this, simply replace letter a by white ball, b by blue ball, c by red ball, d by yellow ball and e by green ball. The permutation carries the white ball from location 1 to location 4, blue ball from 2 to 5,...etc. As a result [5.2] is true for the permutation of the colored balls.

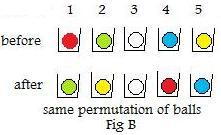
In the adjacent figure (Fig B) the balls start out in a different order in the top row. But the same permutation given by [5.2] rearranges them to produce the bottom row.

A working definition for permutation:
[5.1] A permutation of a finite collection of objects is a rearrangement of those objects.

This assumes that the objects are in a row (array), one after the other. There is an object in the first position, there is another object in the second position,...,there is an object in the last position. This is needed so that a complete rearrangement can happen.

In the process of a permutation, no objects are lost or added to the collection. The objects after the permutation has happened, are the same as those before the permutation takes action. There arrises a one-to-one correspondence between the objects before the permutation and the objects after the permutations by their positions:
the object in the first position before the permutation corresponds (~) to the object in the first position after the permutation,
the object in the second position before the permutation corresponds (~) to the object in the second position after the permutation,
............... the object in the last position before the permutation corresponds (~) to the object in the last position after the permutation.

In Fig A,
   the white ball ~ yellow ball (because both are in the first position.);
   the blue ball ~ green ball;
   the red ball ~ red ball;
   the green ball ~ white ball;
   the green ball ~ the blue ball.
The relation ~ is actually a one-to-one correspondence. This could be rewritten as

1 <--> 4
2 <--> 5
3 <--> 3
4 <--> 1
5 <--> 2
This leads to a revision of [5.1]:

[5.2a] A permutation is a one-to-one correspondence between a finite set and itself. The length of a permutation is the number of elements in that finite set.

The permutation in the above examples has length 5.

Recall that a transformation (function) is non-singular if it is a one-to-one correspondence. The following is a shorter definition, and will be used later.

[5.2b] A permutation is a non-singular transformation on a finite set.

The transformation k -> -k on the set J of all integers is non-singular but is not a permutation. That the set be finite is an important part of the definition of a permutation and will be needed in discussions later.

Suppose some permutation has mixed up the integers 1,2,3,4,...,n in Pn to produce an array '1 a2 a3 a4 ... an'. Three forms for writing a permutation have been introduced:

[5.3a] array

'a1  a2  a3  a4 ... an'
[5.3b] two row table (matrix):
1     2     3    4 ...  n
a1  a2  a3  a4  ... an 
This notation shows clearly any fixed points of the permutation. It is any number in the top row that is the same as a number below it in the bottom row.

[5.3c] function (arrow) notation:

1 --> a1,   2 --> a2,   3 --> a3,   4 --> a4 ... n --> an
Actually this function satisfies the definition of a one-to-one correspondence. This condition has been included as a part in definition [5.2a]. This notation also shows any fixed point.

On any finite set the identity transformation is a permutation. It leaves every element fixed. On P6 the identity permutation in array notation is '1 2 3 4 5 6' and in the two row notation:

1   2   3   4   5   6
1   2   3   4   5   6.

There are two more notations, both borrowed from graph theory, which is discussed in another volume.
[5.3d] Click here for a discussion about incidence matrices.

To discuss the
[5.3e] cyclic notation,
actual permutations are needed. Consider the permutation

'9 4 5 6 1 3 2 7 8'
of length 9. In function notation this becomes
1 --> 9
2 --> 4
3 --> 5
4 --> 6
5 --> 1
6 --> 3
7 --> 2
8 --> 7
9 --> 8
Now rearrange the rows and write it in horizontal notation so that the numbers on both sides of each comma are equal:
1 --> 9,   9 --> 8,   8 --> 7,   7 --> 2,   2 --> 4,   4 --> 6,   6 --> 3,   3 --> 5,   5 --> 1
This can be written as a "chain of arrows" by omitting commas and duplications of numbers:
1 --> 9 --> 8 --> 7 --> 2 --> 4 --> 6 --> 3 --> 5 --> 1
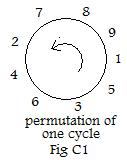It is not necessary to continue the chain any longer, because it will repeat this part of the chain again and again. This can be condensed further to a cyclic notation:
(1 9 8 7 2 4 6 3 5)
In this notation enclosed in parentheses, it is understood that after the last number 5 the first number 1 would appear to make the chain of arrows, which is horizontal. The cyclic notation can be placed around a circle, as is shown in the figure to the right.


For the permutation '7 8 1 3 9 6 4 5 2' two circles are needed as shown in Fig C2 below. The function notation is:
1 --> 7
2 --> 8
3 --> 1
4 --> 3
5 --> 9
6 --> 6
7 --> 4
8 --> 5
9 --> 2
Starting with 1, the following chain of arrows is produced:
1 --> 7 --> 4 --> 3 --> 1
Obviously there are some missing integers. For example, 2 is missing from this chain. Start with 2:
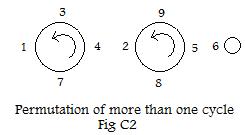2 --> 8 --> 5 --> 9 --> 2
The number 6 is missing from both chains.
6 --> 6
All nine integers have been "used." The cyclic notation for this permutation is
(1 7 4 3)(2 8 5 9)(6)
See Fig C2. The last cycle of one number (6) is often omitted. Cycles of just one number are omitted, and they always represent fixed points.

However (1) is the cyclic notation for the identity permutation. Expanded it looks like (1)(2)(3)....(n). A listing of all the one-element cycles may be used to indicate the length of the permutation.

Click here for a discussion of a faster method of converting array notation for a permutation to cyclic notation.

Notice that if more than one cycle is involved to represent a permutation, those cycles are disjoint. In an intuitive sense, all the cycles of a permutation of length n together form a partition of the set Pn.

Most discussions involve rearranging the integers in the set Pn. For any other finite set of n elements, it is possible to "attach" the numbers in Pn by counting the elements. Then the permutation can "act" on these integers in Pn. More exactly, these attachments create a one-to-one correspondence between that finite set and Pn. Through that one-to-one correspondence any discussion about permutations on the finite set can be "transferred" to discussions about corresponding permutations on Pn. In other words, most of the discussions will involve permutations on Pn, without any loss of generality.

In some situations the number and listing of all permutations on a set becomes important..
On P1 there is exactly one permutation, the identity transformation: '1'
On P2 there are exactly two permutations:     '1 2'    and   '2 1'
On P3 there are exactly six permutations:     '1 2 3',    '1 3 2'   '2 1 3'   '2 3 1'   '3 1 2'   '3 2 1'

Sometimes, the number of all permutation on the same set is needed.
[5.4] On a set of n distinct objects there are n! permutations.

factorials
n! means the product of all the positive integers from 1 to n:   n! = 1x2x3x...xn. 1! = 1, 2!=2, 3! = 6, 4!=24, 5! = 120, 6! = 720,.. . In future discussions it will be convenient to define 0! = 1. As the positive integer n increases, its factorial n! increases extremely fast. For example 13! = 6 227 020 800, a number in the billions! It is so large that some computers cannot accept it (using some programming languages). Click here for more discussion of factorials, including a derivation of [5.4].

The above discussions involve permutations in isolation. With two permutations (or the same permutation twice) their product can be formed and computed by the usual method for products of functions.

[5.5] Closure The product of any two permutations on the same set is a is a permutation on that set.

This is true since the product of one-to-one correspondences is a one-to-one correspondence.

[5.6] Inverse The inverse of a permutation one a set is a permutation on that set.

This is true because a permutation is non-singular.

[5.7] In summary, the collection of all permutations on the same finite set has the four algebraic properties:
   [a]The product of any two permutations is a permutation [5.5].
   [b] Product is an associative operation.
   [c] The identity transformation is a permutation.
   [d] The inverse of a permutation is a permutation [5.6].