Section 2 One-To-One Correspondences
In this section a method is developed to compare the sizes of two sets, more exactly, to determine if they have the same number of elements. The following situation contains the simple idea for doing this.
 [2.1]
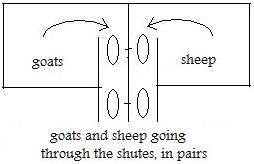
Two farmers had herds of animals. One farmer had a herd of goats, the other farmer, a herd of sheep. They thought that the sizes of the herds showed that there was the same number of animals in them. The farmers wanted to verify this. However, neither farmer could count 1,2,3,... . To solve this problem, the herds were separated, and the animals forced to go through two parallel chutes as shown. One from the herd of goats and one from the herd of sheep at the same time through the chutes, and this is done, one by one, until all the animals from both herds had passed through the gates. ( No animal could go twice through a chute.) That would prove that the numbers of animals both herds are the same (without counting).
[2.1]
Two farmers had herds of animals. One farmer had a herd of goats, the other farmer, a herd of sheep. They thought that the sizes of the herds showed that there was the same number of animals in them. The farmers wanted to verify this. However, neither farmer could count 1,2,3,... . To solve this problem, the herds were separated, and the animals forced to go through two parallel chutes as shown. One from the herd of goats and one from the herd of sheep at the same time through the chutes, and this is done, one by one, until all the animals from both herds had passed through the gates. ( No animal could go twice through a chute.) That would prove that the numbers of animals both herds are the same (without counting).
The animals going through the chutes creates an ordered pair, the first coordinate is the goat and the second coordinate is the sheep. This collection of ordered pairs forms a relation-set and therefore a relation between the herd of goats and the herd of sheep. All the goats are paired with all the sheep, so the relation is actually a function from the herd of goats onto the herd of sheep. Clearly, distinct goats are related to distinct sheep. So this function is one-to-one. One on one relations between elements of two sets are very common.
[2.2a]
A one-to-one correspondence between the two sets is a relation between the two sets such that
(i)each element of the first set is related to a single element in the second set;
(ii)all of the elements of the second set are involved in the relation.
[2.2b]
In the truth set of ordered pairs of a one-to-one correspondence between two sets,
(i)each element of the first set appears once and only once as first coordinates;
(ii)each element of the second set appears once and only as second coordinates.
There exists a one-to-one correspondence between P4 and any set of 4 elements.
[2.3]
For example if the second set is S = {A,B,C,D}, then a "natural" one-to-one correspondence is:
1 <-> A
2 <-> B
3 <-> C
4 <-> D
The truth set of ordered pairs for this relation between P4 and S is:
{(1,A), (2,B), (3,C), (4,D)}
Clearly the numbers 1,2,3,4 appear once and only once as first coordinates, and the letters A,B,C,D appear once and only once as second coordinates.
A notation <-> used in these discussions is used for one-to-one correspondences. f: U <-> V may be used to indicate that f is a one-to-one correspondence. Sometimes the name of the relation is written over the notation <->.
There is a natural one-to-one correspondence x <-> 2x between the set P of positive integers and the set {2,4,6,8,10,...} of even positive integers, whose name can be written 2P.
[2.4]
A similar correspondence x <-> 2x exists between the set J of all integers (positive, negative, zero) and the set of even integers 2J = {..., -4, -2, 0, 2, 4, ...}. In fact, there is a natural correspondence x <-> nx between J and nJ for any positive integer n.
Note that the set nJ of multiples of n is different from Jn = {0,1,2, ..., n-1}. Similarly, nPPn = {1,2,3,...,n}.
In definition [2.2a] a one-to-one correspondence is said to be between two sets U and V, and not from one set Uonto the other V. A direction is not indicated. Also, colors have not been used to distingish domain and range. The opening example [2.1] shows the unimportance of distinguishing domain and range for a one-to-one correspondence. The one-by-one relation is of goats to sheep or of sheep to goats, it does not matter. Consider the relation-set of a one-to-one correspondence (definition [2.2b]) between these two sets. A typical ordered pair in the set is (u,v). Suppose the coordinates of every pair are switched (v,u). Then, then all the elements of set V appear once and only once as first coordinates, and all the elements of set U appear once and only once as second coordinates. Therefore, this new relation-set is the relation-set for another one-to-one correspondence between the two sets, but, in some sense, in the reverse order. Let us call it the inverse correspondence.
In the above example [2.3]of a one-to-one correspondence between P4 and S = {A,B,C,D}, the inverse correspondence is
A <---> 1
B <---> 2
C <---> 3
D <---> 4
[2.5] Theorem
If two functions f and g are both one-to-one correspondences (and g is conformable with f), then their product gf is one-to-one correspondence.
This theorem follows immediately from two theorems in the previous section [2.5] and [2.6].
Click here for examples of products of one-to-one correspondences.
[2.6]
The inverse correspondence of a one-to-one correspondence f: U <--->V is a one-to-one correspondence f -1: V<--->U obtained by reversing related (by f) elements in the two sets U,V.
If f relates an element u to an element v (u ~ v) then f -1 relates v to u (v ~ u).
[2.7]
Every non-empty set has a natural one-to-one correspondence between the set and itself. It relates each element in the set with itself: u <---> u for each element u in a set U. It is denoted as IU. If there is no confusion I denotes the correspondence. It is called the identity transformation (on U)
The identity transformation on the set P4 is:
in <---> notation:
1 <---> 1
2 <---> 2
3 <--->3
4 <---> 4
and in function notation:
I(1) = 1
I(2) = 2
I(3) = 3
I(4) = 4
It is obvious that the inverse I -1 = I. Interchanging the coordinates of all ordered pairs in the relation-set of I produces no change. Then I and its inverse I-1 have the same relation-set. Therefore the two transforations are equal.
Recall that the number 1 is the identity for numerical multiplication. Its basic property is: x*1 = x = 1*x. Multiplying any number by 1 simply produces that same number back again. A similar situation exists with multiplying the identity transformation with functions (they need not be one-to-one correspondences).
Suppose f:: U ---> V and I is the identity transformation on set U. Then f*I(u) = f(u) for any element u in U. This shows that f*I and f carry each element in U onto the same element in V. Now let I be the identity transformation on V. Let v be the image of u. Then I*f(u) = I(v) = v = f(u). Then functions I*f and f cary each element in U onto the same element in V. Therefore they are equal. Therefore, f*I = f = I*f . Products of I with functions act like products of 1 with numbers.
[2.8] If the product of any function and I can be made (are conformable), then that product is equal to the function alone. f *I = f. Similarly, if the product of I an any function can be made (are conformable) then that product is equal to the function alone. I*g = g.
Also recall that the product (1/x) * x = x/x = 1 and x * (1/x) = x/x = 1 and 1/x = x -1. The reciprocal is also the inverse of a number. The product of a number and its inverse is 1. Also the product of the inverse and the number is 1.
There is a similar situation with the one-to-one transformations.
[2.9]
The product of a one-to-one correspondence and its inverse is the identity transformation (on the domain). The product of the inverse of a one-to-one transformation and that one-to-one transformation is the identity transformation (on the range).
Let u be any element in set U and let
Let f: U <---> V be a one-to-one correspondence between sets U and V. For any element u in U let vbe its image in V. Then f(u) = v and f -1(v) = u.
Then f*f -1(v) = f(u) = v = I(v). This shows that f*f -1 and I carry each element in set V onto itself. So they are equal. Similarly for
f -1*f(u) and I(u).
Then [2.9] suggests the inverse notation for the inverse function.
 [2.1]
Two farmers had herds of animals. One farmer had a herd of goats, the other farmer, a herd of sheep. They thought that the sizes of the herds showed that there was the same number of animals in them. The farmers wanted to verify this. However, neither farmer could count 1,2,3,... . To solve this problem, the herds were separated, and the animals forced to go through two parallel chutes as shown. One from the herd of goats and one from the herd of sheep at the same time through the chutes, and this is done, one by one, until all the animals from both herds had passed through the gates. ( No animal could go twice through a chute.) That would prove that the numbers of animals both herds are the same (without counting).
[2.1]
Two farmers had herds of animals. One farmer had a herd of goats, the other farmer, a herd of sheep. They thought that the sizes of the herds showed that there was the same number of animals in them. The farmers wanted to verify this. However, neither farmer could count 1,2,3,... . To solve this problem, the herds were separated, and the animals forced to go through two parallel chutes as shown. One from the herd of goats and one from the herd of sheep at the same time through the chutes, and this is done, one by one, until all the animals from both herds had passed through the gates. ( No animal could go twice through a chute.) That would prove that the numbers of animals both herds are the same (without counting).