[1.1a] Let U and V denote sets that are universes. Let u be any element from the first universe U and let v be any element from the second universe V. Then (u,v) is an ordered pair from U and V. The part u is called the first coordinate of the ordered pair, and v is the second coordinate of the ordered pair. The symbol UxV will denote the set of all ordered pairs whose first coordinates are taken from U and second coordinates taken from V. It is called the product set or product of U and V.
For example let U = {1,2,3} and V = {Washington,London}. Then
UxV = (1,Washington), (1,London), (2,Washington), (2,London), (3,Washington), (3,London)}
Clearly, if the first universe has m elements and the second universe has n elements then their product set has mn elements. This motivates the word "product" in "product set."

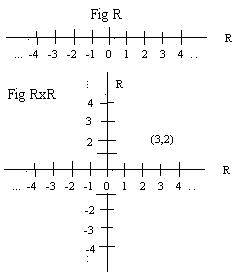
Another example of a product set is the coordinate plane RxR of elementary algebra. In the adjacent drawing are two figures. In Fig R is the coordinate line where points are located by real numbers.
In Fig RxR the coordinate plane RxR contains this embedded horizontal line of the previous figure, and an embedded vertical copy of it. It is traditional to call the horizontal line the x-axis and the vertical line, the y-axis. For any ordered pair (x,y) the first coordinate x is taken from the x-axis and the second coordinate y is taken from the y-axis. Some definitions and facts about product sets are motivated by familiar facts about RxR.
[1.1b]
In any product set, equal ordered pairs have equal first coordinates and equal second coordinates.
In general, interchanging the first and second coordinates produces a different ordered pair. Therefore, VxU is usually different from UxV.
Many of the definitions and facts about products of two sets can be extended to more than just two. UxVxW is obviously a collection of all triples (u,v,w) where u is taken from set U, v from set V and w from set W. Two triples are equal if and only if their respective coordinates are equal:
RxRxR denotes coordinate space of all triples (x,y,z). RxRxRxR is hyper-space of four dimensions.
(Jim,USA)-F (Jim,England)-T (Steve,USA)-T (Steve,England)-F (Robert,USA)-T (Robert,England)-T (Ruth,USA)-F (Ruth,England)-FThe collection of ordered pairs that have been assigned a T form a subset of UxV:
[2.1]
An ordered pair is in relation-set if and only the first coordinate is truly related to the second coordinate.
The statement x ~ y has variables in it. Therefore it is an open statement in two variables:
There are two extremes for the relation-set. (1) The relation-set is the whole product set UxV. This means that every element in U is related to every element in V. The statement u ~ v is always true for u in U and v in V. (2) The relation-set is empty. Then no element in U is related to any element in V. These extreme situations usually are of little interest.
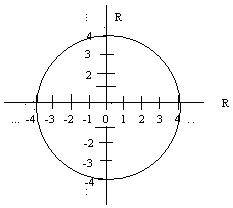
A relation-set that has a familiar geometric shape in RxR is the circle x2 + y2 = 16. It has center at the origin and radius 4. The relation-set for x2 + y2 <= 16 is a disk, a circle and its interior.
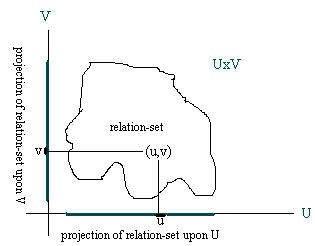 The figure to the right is a "generalized" relation-set without any specific shape. It gives some visual support for a discussion here. The dark line segments represent all the coordinates needed for all the ordered pairs (u,v) in the relation-set. The way the figure is drawn, the first coordinates of the relation-set do not involve all of the universe U. And the second coordinates of the relation-set do not involve all of V. Let the projection of the relation-set upon U be the subset of all elements of U that are used in the first coordinates of all ordered pairs in the relation-set. as first coordinates of all ordered pairs in the relation-set. Similarly, let the projection of the relation-set upon V be the subset of all elements of V that are used as second coordinates of all ordered pairs in the relation-set.
The figure to the right is a "generalized" relation-set without any specific shape. It gives some visual support for a discussion here. The dark line segments represent all the coordinates needed for all the ordered pairs (u,v) in the relation-set. The way the figure is drawn, the first coordinates of the relation-set do not involve all of the universe U. And the second coordinates of the relation-set do not involve all of V. Let the projection of the relation-set upon U be the subset of all elements of U that are used in the first coordinates of all ordered pairs in the relation-set. as first coordinates of all ordered pairs in the relation-set. Similarly, let the projection of the relation-set upon V be the subset of all elements of V that are used as second coordinates of all ordered pairs in the relation-set.
In the example just before [2.1] the projection of the relation-set upon U is the set {Jim, Steve, Robert}. The projection upon V is all of V={USA,England}. The projection of the circle x2 + y2 = 16 are line segments from -4 to +4 on the horizontal x-axis and on the vertical y-axis. The solid disk has the same projections.