Until now the only numbers that have been involved with graphs have been the positive integers. They were used as labels on all the nodes in graphs. In some cases their ordering affected a traversing a labeled graph But most often the integers served merely as identification symbols for the nodes of graphs. In that service they allow the writing of computer programs to process the graphs.

But labeled graphs can represent more situations if numbers can be assigned to nodes and/or edges (or arcs). Sometimes information in the form of text is assigned to nodes as is done with some trees. A weighted graph or a graph with weights has numbers or text assigned to its nodes or links. Usually the labels on its nodes are not considered to be weights.

In Fig 3.1a a weight of 240 has been assigned to an edge. Think of the number 240 as representing physical distance between two towns with the labels 4 and 7. In Fig 3.1b the number 50 represents the quantity of water flowing each second through a pipe from town 6 to town 8. It is convenient to write the weights along side the edges or arcs in a drawing of a graph.

Fig 3.1c shows a labeled ugraph with weights attached to the edges. If the weights are interpreted as physical distances, then obviously the edges are not drawn to scale. For example edges 2-4 and 3-4 have the same length in the drawing yet they represent vastly different distances. This lack of proper scaling is done throughout graph theory, because it does not produce errors in the processing of weighted graphs.

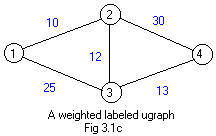
It is natural to add up the weights to get a result for a path. For example the sum of the weights for path 1-3-2-4 is 25 + 12 + 30 = 67. If the weights 25,12,30 represent physical distances, then 67 is a physical distance. It represents the physical length of the path 1-3-2-4. The weighted length of a path is the sum of the weights assigned to the edges or arcs that make up the path.

There is another length of a path. The graphical length of a path is the number of edges or arcs in the path. The path 1-3-2-4 is made up of three edges, so the graphical length is 3. The graphical length is determined from the basic structure of a graph, and not from weights assigned to the edges or arcs.

The distinction between the two lengths of the same path becomes noticeable when working with the idea of the shortest path between two nodes. The shortest weighted path from node 1 to node 4 is 1-2-3-4 because its sum 10 + 12 + 13 equals 35. Any other path from node 1 to node 4 has longer weighted length. For example, path 1-2-4 has weighted length 40. Yet this path 1-2-4 has only two edges. This path has a shorter graphical length than 1-2-3-4. The number of dashes in the horizontal arithmetic notation for a path is equal to the graphical length of the path.

Both lengths, weighted and graphical, of a path with a loop are longer than the lengths of the path with the loop removed from that path.

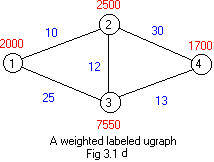
In Fig 3.1d the population figures of the four towns has been indicated. They are written along side their respective nodes. If distances between towns are not important those numbers could have been omitted from along side the edges in Fig 3.1d.

The short form of the adjacency array for the ugraph in Fig 3.1d without weights is:

S   1,2,3,  2,3,4,   3,4,   4,   0,0

S()  1,2,3,(2000,10,25),   2,3,4,(2500,12,30),   3,4,(7550,13),   4,(1700),   0,0

The number of weights inside the parentheses is equal to the number of integers in the cluster just before the parentheses. The weight is assigned to the leading integer, which is the label for a node, is placed first inside the parentheses. The blue weights are assigned to edges, not to nodes.

Recall that the short form is an abbreviation. A modified form of this and the weights under it are:
S   1,     1-2   1-3           2,    2-3   2-4         3,   3-4           4,           0,0
() 2000  10     25         2500  12     30       7550  13         1700
It is easier to type the S() array form with weights inside parentheses than to type the S array and the weights written under it. For weighted labeled graphs the S(), F() and D() arrays will be used usually without colors.