Problems for Chapter 1

Problems for section 1.1

Return to Chapter01 / section 1.1


Problems for section 1.2




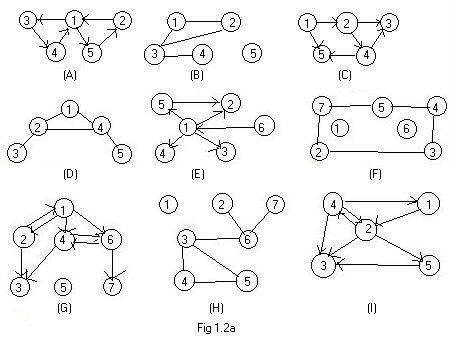
In Fig 1.2a some of the graphs are ugraphs and others are digraphs. For each ugraph write down the full adjacency array and the short adjacency array. For each digraph write down the adjacency array. (Answers are given below.)











Return to Chapter01 / section 1.2

Problems for section 1.3

Problem 1.3a

In the drawing Fig 1.3a six pairs of ugraphs are shown. Which pairs are equivalent?


Problem 1.3b

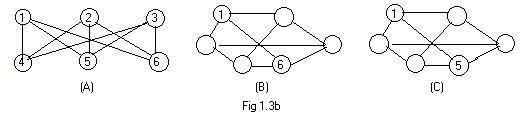In the drawing Fig 1.3b the first (A) is a labeled ugraph. Some of the nodes in drawings (B) and (C) are labeled. Finish labeling (B) and (C) so that all three ugraphs have the same adjacency arrays.

Problem 1.3c

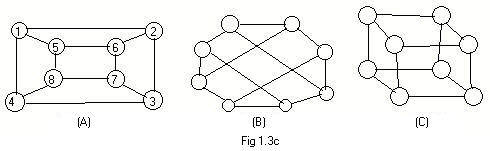In the drawing Fig 1.3c the first (A) is a labeled ugraph. Label all the nodes in (B) and (C) so that all three ugraphs have the same adjacency arrays.




Problem 1.3d

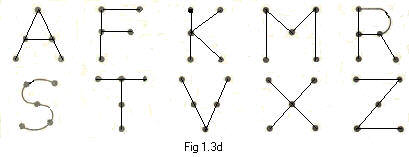
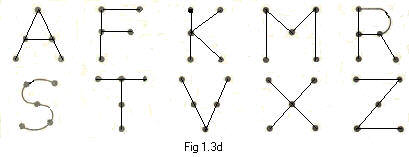The following letters form ten ugraphs. On each the five small solid black circles are thenodes.
(a) Copy A and R to paper, replacing the black circles by ordinary circles big enough to contain integers. Label the vertices in A with integers 1,2,3,4,5. Then find a labeling of R with the same five integers so that A and R have the same short adjacency arrays. (This shows that A and R are equivalent ugraphs).
(b) To what ugraph F equivalent?
(c) To what is the letter ugraph K equivalent?
(d) In the same way show that the remaining four letters form two pairs of equivalent ugraphs

Problem 1.3e True or False ?
(A) All ugraphs with exactly 3 nodes and exactly 2 edges are equivalent?
(B) The ugraph in Fig 1.3e is NOT equivalent to any ugraph in figure Prob1.3f.
(C) Any ugraph with exactly 4 nodes and exactly 3 edges is equivalent to one of the ugraphs shown in Fig 1.3f.
(D) If two labeled ugraphs have the same (short) adjacency arrays then they are equivalent.
(E) All complete ugraphs with exactly 5 nodes are equivalent May the number 5 be replaced by any positive integer to get a true statement?

Problem 1.3f Draw two non-equivalent ugraphs with exactly 4 nodes and 2 edges each.


Answers to problem 1.2a (S=short adj array for a ugraph, F=full adj array for a ugraph, D=adj array for a digraph)
(A) D, 1,3,5,  2,1,  3,4,  4,1,  5,2,   0,0
(B) S,  1,2,3,  2,3,  3,4,  4,  5,0,   0,0  /   F,  1,2,3,  2,1,3,  3,1,2,4,  4,3,  5,0,   0,0
(C) D,  1,2,5,  2,3,4,  3,  4,3,5,  5,   0,0
(D) S,  1,2,4,  2,3,4,  3,  4,5,  5,   0,0  /   F,  1,2,4,  2,1,3,4,  3,2,  4,1,2,5,  5,4,   0,0
(E) D,  1,2,3,4,5,  2,  3,  4,  5,2,  6,1,   0,0
(F) S,  1,0,  2,3,7,  3,4,  4,5,  5,7,  6,0,  7,   0,0   /  F,  1,0,  2,3,7,  3,2,4,  4,3,5,  5,4,7,  6,0,  7,2,5,   0,0
(G) D,  1,2,4,6,  2,1,3,  3,  4,3,6,  5,0,  6,4,7,  7,   0,0
(H) S,  1,0,  2,6,  3,4,5,6,  4,5,  5,  6,7,  7,   0,0   /  F,  1,0,  2,6,  3,4,5,6,  4,3,5,  5,3,4,  6,2,3,7,  7,6,   0,0
(I) D  1,2,  2,3,4,5,  3,  4,1,2,3,  5,3,   0,0

Answers to problem 1.3a
The pairs of ugraphs in B,D,E,F are equivalent. The pairs in A,C are not equivalent.

Answers to problem 1.3b


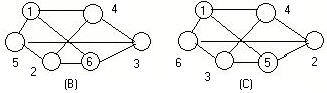
Notice that every node has degree three.


Answers to problem 1.3c


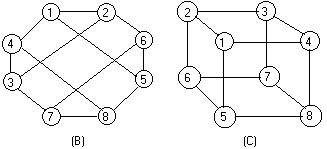
There are more than one completed labeled graph for (B) and (C). One solution is given to the right. Notice that every node must have degree three.

Answers to problem 1.3d
The following pairs of letters form equivalent ugraphs:
A,R  F,T  K,X  M,V  S,Z

Return to Chapter01 / section 1.3