Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer Programs
Return to index of all chapters in this volume
Volume F Chapter 3
Digraphs
Section 1: Graphs with Directed Links
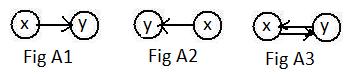 There are situations that allow motion to go in one direction but not in the reverse direction. One-way streets, water flowing down a hill, and direct current electricity are examples. The notation for such a situation is shown in the adjacent Fig A1 and Fig A2.. Motion can go from object x to object y but without any other information, it cannot go from object y back to object x. These are examples of directed links, an outgoing link from object x which is also an incoming link to object y. The notation
x→y and y←x
will be used in discussions. The term "neighbor" does not apply to objects connected by a directed link.
There are situations that allow motion to go in one direction but not in the reverse direction. One-way streets, water flowing down a hill, and direct current electricity are examples. The notation for such a situation is shown in the adjacent Fig A1 and Fig A2.. Motion can go from object x to object y but without any other information, it cannot go from object y back to object x. These are examples of directed links, an outgoing link from object x which is also an incoming link to object y. The notation
x→y and y←x
will be used in discussions. The term "neighbor" does not apply to objects connected by a directed link.
In Fig A3, motion can go from either object to the other, like cars on a two-way street. The bi-directional links of the last two chapters are replaced in this chapter by the pair of directed links pointing in opposite directions.
 Sometimes it is useful to count the links involved with an object. The indegree of an object is the number of incoming links. The outdegree of an object is the number of outgoing links. In Fig B the indegree of the object is 3 and the outdegree is 2. If the two outgoing links are removed then the object would have indegree = 3 and outdegree = 0. In this chapter there will be no objects with indegree = 0 and outdegree = 0 which are isolated objects.
Sometimes it is useful to count the links involved with an object. The indegree of an object is the number of incoming links. The outdegree of an object is the number of outgoing links. In Fig B the indegree of the object is 3 and the outdegree is 2. If the two outgoing links are removed then the object would have indegree = 3 and outdegree = 0. In this chapter there will be no objects with indegree = 0 and outdegree = 0 which are isolated objects.
The term "loop" has a special meaning when directed links are involved.
 Each object in any loop has exactly one outgoing link to another object in the loop. Fig XXa and Fig XXb show such loops. Motion can start in any object and traverse the entire loop to return to the starting object.
But in Fig XXc and in Fig XXd there there is no loop. In each of those figures one object* has no outgoing link to another object in the collection. Motion cannot start and leave such an object* to visit another object in the collection.
Each object in any loop has exactly one outgoing link to another object in the loop. Fig XXa and Fig XXb show such loops. Motion can start in any object and traverse the entire loop to return to the starting object.
But in Fig XXc and in Fig XXd there there is no loop. In each of those figures one object* has no outgoing link to another object in the collection. Motion cannot start and leave such an object* to visit another object in the collection.
Removal of any link in Fig XXa or Fig XXb produces a figure without a loop.
 [3.1] (Digraph) A digraph is a graph with a finite number of objects and directed links.
[3.1] (Digraph) A digraph is a graph with a finite number of objects and directed links.
In the Fig C is an unlabeled digraph with 6 objects.
(Can the reader apply integer-names from N6 to the objects so that
1→2→3→4→5→6
is a path in the graph? It is Hamiltonian. Find a second Hamiltonian path containing every object once and only once.)
In this chapter only connected digraphs are discussed. A digraph is connected if and only if upon replacement of all directed links by bi-directional links a connected graph is the result.
 The six objects in Fig C have been given integer-names as shown in Fig D. Then object 5 has indigree=1 and outdegree=2. Object 3 has indegree=1 and outdegree=2. Using only outgoing links it is possible to construct an adjacency array for this graph:
The six objects in Fig C have been given integer-names as shown in Fig D. Then object 5 has indigree=1 and outdegree=2. Object 3 has indegree=1 and outdegree=2. Using only outgoing links it is possible to construct an adjacency array for this graph:
-1,2,4, -2,5, -3,2, -4,1, -5,4,6, -6,3
Enclosing the above array in brackets [ ] makes it input data for the computer.
All the objects in the graph are represented in the array by means of the negative integers. After each negative integer are positive integers that denote the objects pointed to by the outgoing link of the object with the negative integer. There is just one and only one adjacency array for a digraph, no long and short arrays.
In a directed graph a path joining two objects is a sequence of objects between every pair of which is a directed link, except for the given objects. The first given object has a single outgoing link and the second given object has a single incoming link.
 In a digraph the directed links may impose severe restrictions upon formation of any path. A link has been removed in Fig D to produce Fig. E. As a result, there still is path from object 2 to object 1, but no path from object 2 to object 3.
In a digraph the directed links may impose severe restrictions upon formation of any path. A link has been removed in Fig D to produce Fig. E. As a result, there still is path from object 2 to object 1, but no path from object 2 to object 3.
[1.2] (reachable objects) In a digraph a second object is reachable from a first object if there is a directed path from the first object to the second.
Objecct 1 is reachable from object 2, but object 3 is not reachable from object 2.
Section 2: Maximum flow between objects in a digraph
 It is quite possible that the directed links of a digraph have positive weights assigned to them. But those weights have a different interpretation than weights given in previous chapters. Here they indicate the maximum rate a substance may move from one object to another object. A prime example is water flowing through a pipe. In these discussions that maximum rate allowed by the link is called the capacity of the link. In Fig F are three directed links with capacities 9, 5, 8 gallons/second. (Consider the links represent pipes of different diameters.) The maximum flow from object 1 to object 4 along the indicated path is the smallest of the three capacities, namely 5 gallons/second. Then this flow is not using 4 gallons/second of the capacity 9 of the link from object 1 to object 2, and not using 3 gallons/second of the capacity 8 of the link from object 3 to object 4. The flow through link from objects 2 to 3 is at the maximum 5 that the pipe can carry, and the flow is said to be at capacity there, and the link is saturated. The flow in the other two links is at less than those capacities.
It is quite possible that the directed links of a digraph have positive weights assigned to them. But those weights have a different interpretation than weights given in previous chapters. Here they indicate the maximum rate a substance may move from one object to another object. A prime example is water flowing through a pipe. In these discussions that maximum rate allowed by the link is called the capacity of the link. In Fig F are three directed links with capacities 9, 5, 8 gallons/second. (Consider the links represent pipes of different diameters.) The maximum flow from object 1 to object 4 along the indicated path is the smallest of the three capacities, namely 5 gallons/second. Then this flow is not using 4 gallons/second of the capacity 9 of the link from object 1 to object 2, and not using 3 gallons/second of the capacity 8 of the link from object 3 to object 4. The flow through link from objects 2 to 3 is at the maximum 5 that the pipe can carry, and the flow is said to be at capacity there, and the link is saturated. The flow in the other two links is at less than those capacities.
 In Fig G object 1 is the source of water. It is desirable to send water to object 5 called the sink. There are two obvious, directed paths for the flow of water to travel. Along the upper path
In Fig G object 1 is the source of water. It is desirable to send water to object 5 called the sink. There are two obvious, directed paths for the flow of water to travel. Along the upper path
1→2→3→5
the maximum flow allowed is 6. But along the lower path
1→4→5
the maximum flow allowed is 1.
Since 6 > 1 more water can flow along the upper path than going along the lower path.
 The major topic in this section is to find the directed path from source to sink that allows maximum flow. This statement implies that the sink must be reachable from the source. Also the source has a positive outdegree. The sink is just the opposite, positive indegree. All this is independent of the labelling of the objects with integer-names. For example, Fig H is produced from Fig G by removing all labels on objects and assigning labels "source" and "sink." The maximum flow from source to sink along the upper path is 6 and along the lower path is 1.
The maximum flow going any way from source to sink is along the upper path because 6 > 1.
The major topic in this section is to find the directed path from source to sink that allows maximum flow. This statement implies that the sink must be reachable from the source. Also the source has a positive outdegree. The sink is just the opposite, positive indegree. All this is independent of the labelling of the objects with integer-names. For example, Fig H is produced from Fig G by removing all labels on objects and assigning labels "source" and "sink." The maximum flow from source to sink along the upper path is 6 and along the lower path is 1.
The maximum flow going any way from source to sink is along the upper path because 6 > 1.
However, for use of the computer the labels are needed. In this chapter the optional labelling is to assign the source the integer-name 1, and the sink, the largest of all integer-names (n if there are n objects).
 Sometimes it is useful to count the links involved with an object. The indegree of an object is the number of incoming links. The outdegree of an object is the number of outgoing links. In Fig B the indegree of the object is 3 and the outdegree is 2. If the two outgoing links are removed then the object would have indegree = 3 and outdegree = 0. In this chapter there will be no objects with indegree = 0 and outdegree = 0 which are isolated objects.
Sometimes it is useful to count the links involved with an object. The indegree of an object is the number of incoming links. The outdegree of an object is the number of outgoing links. In Fig B the indegree of the object is 3 and the outdegree is 2. If the two outgoing links are removed then the object would have indegree = 3 and outdegree = 0. In this chapter there will be no objects with indegree = 0 and outdegree = 0 which are isolated objects.
 Each object in any loop has exactly one outgoing link to another object in the loop. Fig XXa and Fig XXb show such loops. Motion can start in any object and traverse the entire loop to return to the starting object.
But in Fig XXc and in Fig XXd there there is no loop. In each of those figures one object* has no outgoing link to another object in the collection. Motion cannot start and leave such an object* to visit another object in the collection.
Each object in any loop has exactly one outgoing link to another object in the loop. Fig XXa and Fig XXb show such loops. Motion can start in any object and traverse the entire loop to return to the starting object.
But in Fig XXc and in Fig XXd there there is no loop. In each of those figures one object* has no outgoing link to another object in the collection. Motion cannot start and leave such an object* to visit another object in the collection.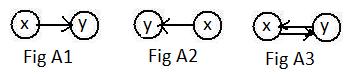 There are situations that allow motion to go in one direction but not in the reverse direction. One-way streets, water flowing down a hill, and direct current electricity are examples. The notation for such a situation is shown in the adjacent Fig A1 and Fig A2.. Motion can go from object x to object y but without any other information, it cannot go from object y back to object x. These are examples of directed links, an outgoing link from object x which is also an incoming link to object y. The notation
There are situations that allow motion to go in one direction but not in the reverse direction. One-way streets, water flowing down a hill, and direct current electricity are examples. The notation for such a situation is shown in the adjacent Fig A1 and Fig A2.. Motion can go from object x to object y but without any other information, it cannot go from object y back to object x. These are examples of directed links, an outgoing link from object x which is also an incoming link to object y. The notation
 [3.1] (Digraph) A digraph is a graph with a finite number of objects and directed links.
[3.1] (Digraph) A digraph is a graph with a finite number of objects and directed links.
 The six objects in Fig C have been given integer-names as shown in Fig D. Then object 5 has indigree=1 and outdegree=2. Object 3 has indegree=1 and outdegree=2. Using only outgoing links it is possible to construct an adjacency array for this graph:
The six objects in Fig C have been given integer-names as shown in Fig D. Then object 5 has indigree=1 and outdegree=2. Object 3 has indegree=1 and outdegree=2. Using only outgoing links it is possible to construct an adjacency array for this graph:
 In a digraph the directed links may impose severe restrictions upon formation of any path. A link has been removed in Fig D to produce Fig. E. As a result, there still is path from object 2 to object 1, but no path from object 2 to object 3.
In a digraph the directed links may impose severe restrictions upon formation of any path. A link has been removed in Fig D to produce Fig. E. As a result, there still is path from object 2 to object 1, but no path from object 2 to object 3.
 It is quite possible that the directed links of a digraph have positive weights assigned to them. But those weights have a different interpretation than weights given in previous chapters. Here they indicate the maximum rate a substance may move from one object to another object. A prime example is water flowing through a pipe. In these discussions that maximum rate allowed by the link is called the capacity of the link. In Fig F are three directed links with capacities 9, 5, 8 gallons/second. (Consider the links represent pipes of different diameters.) The maximum flow from object 1 to object 4 along the indicated path is the smallest of the three capacities, namely 5 gallons/second. Then this flow is not using 4 gallons/second of the capacity 9 of the link from object 1 to object 2, and not using 3 gallons/second of the capacity 8 of the link from object 3 to object 4. The flow through link from objects 2 to 3 is at the maximum 5 that the pipe can carry, and the flow is said to be at capacity there, and the link is saturated. The flow in the other two links is at less than those capacities.
It is quite possible that the directed links of a digraph have positive weights assigned to them. But those weights have a different interpretation than weights given in previous chapters. Here they indicate the maximum rate a substance may move from one object to another object. A prime example is water flowing through a pipe. In these discussions that maximum rate allowed by the link is called the capacity of the link. In Fig F are three directed links with capacities 9, 5, 8 gallons/second. (Consider the links represent pipes of different diameters.) The maximum flow from object 1 to object 4 along the indicated path is the smallest of the three capacities, namely 5 gallons/second. Then this flow is not using 4 gallons/second of the capacity 9 of the link from object 1 to object 2, and not using 3 gallons/second of the capacity 8 of the link from object 3 to object 4. The flow through link from objects 2 to 3 is at the maximum 5 that the pipe can carry, and the flow is said to be at capacity there, and the link is saturated. The flow in the other two links is at less than those capacities.
 In Fig G object 1 is the source of water. It is desirable to send water to object 5 called the sink. There are two obvious, directed paths for the flow of water to travel. Along the upper path
In Fig G object 1 is the source of water. It is desirable to send water to object 5 called the sink. There are two obvious, directed paths for the flow of water to travel. Along the upper path
 The major topic in this section is to find the directed path from source to sink that allows maximum flow. This statement implies that the sink must be reachable from the source. Also the source has a positive outdegree. The sink is just the opposite, positive indegree. All this is independent of the labelling of the objects with integer-names. For example, Fig H is produced from Fig G by removing all labels on objects and assigning labels "source" and "sink." The maximum flow from source to sink along the upper path is 6 and along the lower path is 1.
The maximum flow going any way from source to sink is along the upper path because 6 > 1.
The major topic in this section is to find the directed path from source to sink that allows maximum flow. This statement implies that the sink must be reachable from the source. Also the source has a positive outdegree. The sink is just the opposite, positive indegree. All this is independent of the labelling of the objects with integer-names. For example, Fig H is produced from Fig G by removing all labels on objects and assigning labels "source" and "sink." The maximum flow from source to sink along the upper path is 6 and along the lower path is 1.
The maximum flow going any way from source to sink is along the upper path because 6 > 1.