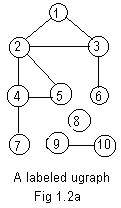
Another method is to list all of the integer labels in order in a column, and then attach to the right of each label all of the neighbors:
Additional Material for Section 1.1
Return to Chapter01
/
section 1.1
=================
Arithmetic ways to record a ugraph
Another method is to list all of the integer labels in order in a column, and then attach to the right of each label all of the neighbors:
## Adjacency List
1,2,3, 2,3 are neighbors of node 1
2,1,3,4,5, 1,3,4,5 are neighbors of node 2
3,1,2,6,
4,2,5,7,
5,2,4,
6,3,
7,4,
8, 8 has no neighbors
9,10,
10,9,
A third method to represent the ugraph is a table in the form of a matrix. The end points of each edge are in the left column and in the upper row:
### Incidence Matrix *
1 2 3 4 5 6 7 8 9 10
1 0 1 1 0 0 0 0 0 0 0
2 1 0 1 1 1 0 0 0 0 0
3 1 1 0 0 0 1 0 0 0 0
* 4 0 1 0 0 1 0 *1 0 0 0
5 0 1 0 1 0 0 0 0 0 0
6 0 0 3 0 0 0 0 0 0 0
7 0 0 0 4 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0 0 0 Node 8 is isolated
9 0 0 0 0 0 0 0 0 0 1
10 0 0 0 0 0 0 0 0 1 0
For example, *4 heads a row and *7 heads a column that intersect at *1. So 4-7 is an edge. But 8 heads a row that interesects with any column at 0. No edge touches 8. Incidence matrices for ugraphs are always symmetric about the main diagonal, because each edge is repeated twice. Pseudo-edges are not included.
The incidence matrix ### is useful as input data to a computer. However it can be very large if there are many nodes. The adjacency list ## also can be used as input data to a computer. Also it requires much less space and is easier to make. Both adjacency lists and incidence matrices are used widely in graph theory.
For a graph to be called labeled, integer labels have been assigned to all of its nodes. Sometimes it is desirable to replace these
The replacing of labels is defined by the following table. The numbers in the top row are replaced by the numbers in the bottom row.
This "brute force" method is not practical on the common desk top computer if the number of nodes is relatively large, say greater than 12. It may not possible for any computer if the number is moderately large, say 20. The number of assignments (permutations=2432902008176640000) is too large, even with "smart" computer programs that eliminate many assignments that give equal adjacency arrays. This suggests that the determination of equivalence of some ugraphs with many nodes and many edges may be difficult if not impossible. Much time may be wasted trying to show that two large or even relatively large ugraphs are equivalent or not equivalent by this method of reassigning integer labels and comparing adjacency arrays.
True or false: all ugraphs with exactly 3 nodes and exactly 2 edges are equivalent?
True or false: any ugraph with exactly 4 nodes and exactly 3 edges is equivalent to one of the ugraphs shown in Fig 1.3d, Fig 1.3e, Fig 1.3f .
True or false: If two labeled ugraphs are equivalent then they have the same adjacency arrays.
True or false: all complete ugraphs with exactly 5 nodes are equivalent May the number 5 be replaced by any positive integer to get a true statement?
Draw two non-equivalent ugraphs with exactly 4 nodes and 2 edges each.
Converting between full and short adjacency arrays
filler
Replacing the integer labels on all the nodes of a labeled graph
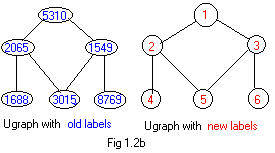old labels with new labels without changing the basic sturcture of the graph. In figure 1.2b are two labeled ugraphs with the same basic structure (in fact almost congruent) but with different integer labels. The old labels on the ugraph are valid but have an appearance of being random and large. The new labels on the ugraph are smaller and more natural.
Table A of replacing labels
5310 2065 1549 1688 3015 8769
1 2 3 4 5 6
A diffierent table B, called the inverse table of A, can be obtained from table A by interchanging rows. Then the inverse table B can be used to restore old labels from the new labels.
Table B of replacing labels
1 2 3 4 5 6
5310 2065 1549 1688 3015 8769
Always replace the numbers in the top row by the numbers in the bottom row.
Return to Chapter01
/
section 1.2
=================
Additional Material for Section 1.3
After assignment of integer labels to one ugraph, theoretically a computer can be used to make all the different assignments to another ugraph and then construct the adjacency arrays for both. It could compare the arrays each time. If the arrays are equal then somehow the computer could indicate how the assignment of integer labels to the second ugraph was made.