Return to main page on affine transformations
Additional Material on Affine Transformations
Orientation of Segments
 For any given a line segment (see Fig 1), any pair of different symbols may serve as labels attached to the endpoints. But in naming the segment one of those symbols is written first or left-most and the remaining symbol is written after the first symbol to its right. This order of naming the endpoints gives an orientation to the segment. For example, if the end points have labels A and B (see Fig 2), then calling the segment AB gives it an orientation. Suppose C and D are labels also attached to the endpoints of the same segment (see Fig 3). Then segment AB and segment CD are the same. CD gives the segment the same orientation as AB because C=A and D=B. If C=B and D=A then CD gives the segment the opposite orientation as AB (see Fig 4). In particular BA gives the segment the opposite orientation as AB. A segment with different orientations is still the same subset of points.
For any given a line segment (see Fig 1), any pair of different symbols may serve as labels attached to the endpoints. But in naming the segment one of those symbols is written first or left-most and the remaining symbol is written after the first symbol to its right. This order of naming the endpoints gives an orientation to the segment. For example, if the end points have labels A and B (see Fig 2), then calling the segment AB gives it an orientation. Suppose C and D are labels also attached to the endpoints of the same segment (see Fig 3). Then segment AB and segment CD are the same. CD gives the segment the same orientation as AB because C=A and D=B. If C=B and D=A then CD gives the segment the opposite orientation as AB (see Fig 4). In particular BA gives the segment the opposite orientation as AB. A segment with different orientations is still the same subset of points.
The idea of same and opposite orientations may be extended to parallel segments.
 Given two parallel line segments with distinct endpoints (see Fig 5). The four endpoints are vertices of a trapezoid (see Fig 6). Any four different symbols may serve as labels attached to the four endpoints (the letters A,B,C,D will be used here). A pair of them identify one of the segments, and the remaining pair of symbols identify the other segment. But as names of segments, each pair must be written from left to right, so that there is a first symbol in each pair. Supply four more segments to join pairs of vertices to form a trapezoid and its two internal diagonals (Fig 6). The first symbols of each pair of symbols are endpoints of one of these supplied segments. (Fig 7 and Fig 8 show two ways of assigning labels to the four endpoints.) Is that supplied segment a side of the trapezoid or a diagonal? If the supplied segments are sides of the trapezoid (AC and BD in FIg 7), then the parallel line segments have the same orientation. If the supplied segments are diagonals of the trapezoid (AC and BD in Fig 8) then the parallel line segments have opposiste orientation.
Given two parallel line segments with distinct endpoints (see Fig 5). The four endpoints are vertices of a trapezoid (see Fig 6). Any four different symbols may serve as labels attached to the four endpoints (the letters A,B,C,D will be used here). A pair of them identify one of the segments, and the remaining pair of symbols identify the other segment. But as names of segments, each pair must be written from left to right, so that there is a first symbol in each pair. Supply four more segments to join pairs of vertices to form a trapezoid and its two internal diagonals (Fig 6). The first symbols of each pair of symbols are endpoints of one of these supplied segments. (Fig 7 and Fig 8 show two ways of assigning labels to the four endpoints.) Is that supplied segment a side of the trapezoid or a diagonal? If the supplied segments are sides of the trapezoid (AC and BD in FIg 7), then the parallel line segments have the same orientation. If the supplied segments are diagonals of the trapezoid (AC and BD in Fig 8) then the parallel line segments have opposiste orientation.
If the segments are on the same line, then construct a parallel line, copy one segment onto the new line and apply the trapezoid rule to those parallel segments that are on different lines.
A Geometric Construction of a One-to-One Correspondence Between Lines
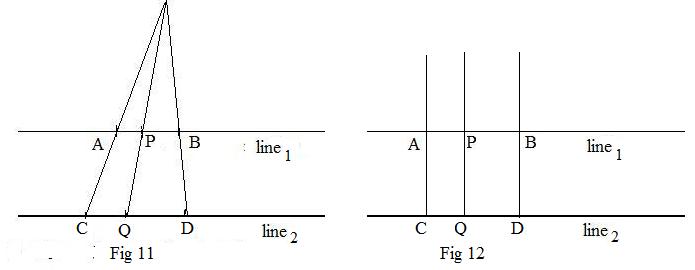 Given two distinct parallel lines. Name them line1 and line2. Also given a pair of distinct points on each line. (If not given then select a pair of distinct points on each line.) Label A,B the points on the first line. Label the pair of points on the second line C,D so that the segments have the same orientation (lines through A,C and B,D do not intersect between the parallel lines). Then lines through A,C and B,D intersect above or below the parallel lines, or those lines are themselves parallel.
Given two distinct parallel lines. Name them line1 and line2. Also given a pair of distinct points on each line. (If not given then select a pair of distinct points on each line.) Label A,B the points on the first line. Label the pair of points on the second line C,D so that the segments have the same orientation (lines through A,C and B,D do not intersect between the parallel lines). Then lines through A,C and B,D intersect above or below the parallel lines, or those lines are themselves parallel.
Case 1: Lines through A,C and B,D intersect (are not parallel). See Fig 11 above.
Let P be any point on line1. Through the point of intersection of lines A,C and B,D and through point P draw a line to intersect line2 at some point Q. As P moves about line1 the corresponding point Q moves about line2. The P,Q movement establishes a one-to-one correspondence between line1 and line2.
Case 2: Lines through A,C and B,D are parallel. See Fig 12 above
In this case through moving point P located on line1 draw a line parallel to line through A,C. It will intersect line2 at Q. Since P can be any point on line1, intuitively speaking, it is as if P moves about all of line1 while the corresponding point Q moves about all of line2. This P,Q relationship establishes a one-to-one correspondence between all of line1 and line2.
Affine transformations and linear transformations
Assume than an origin exists.
(a) All linear transformations are affine transformations.
(b) An affine transformation is a linear transformation if and only if it carries the origin onto itself.
Proof of (a)
Let L be any linear transformation. Let A and B be any points, and P any point on line AB.
Then for some real number λ,
(#) vector AP = λAB
and
(*) p -- a = λ(b -- a).
Let A' = L(A); B'=L(B), P'=L(P); Then a' = L(a); b' = L(b); p' = L(p); Apply linear transformation L to equation (*) to get
(**) p' -- a' = λ(b' -- a').
But this means that
(##) vector A'P' = λA'B'
That λ is the same in equations (#) and (##) means that L preserves proportionality. Hence L is affine.
- - - - - - - - - - - - - - - - -
Proof of (b)
Trivially, if an affine function F is linear then F must carry the origin onto itself.
Looking at the converse, assume that F is affine and carries the origin onto itself. To prove that F is linear. This means that F(λp) = λF(p) for any position vector p and any real number λ
Let q = λp. Then
(&) OQ = λOP
Let P' = F(P), Q' = F(Q), O' = F(O) = O. Apply affine transformation F to equation (&) to get
O'Q' = λO'P'
which is equiivalent to
(&&) OQ' = λOP'
because O' = O (by hypothesis, F carries the origin onto itself). Converting (&&) into an equation of position vectors,
q'=λp' which means F(q) = λF(p) and finally F(λp) = λF(p). Therefore F is linear.



