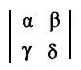
The following is sometimes a useful tool for finding the orientation of directed arcs:
[3.0a] (Positive or negative orientation according to a determinant) In the coordinate plane let P(α,β) and Q(γ,δ) be any pair of points on a circle with center at origin O.
(i)Then directed arc PQ has positive orientation if and only if the determinant
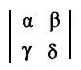
Now suppose P, Q have different coordinates, P(-3,4) and Q(3,4). Then the new values for α,β,γ,δ are
For a discussion supporting these statements click here.
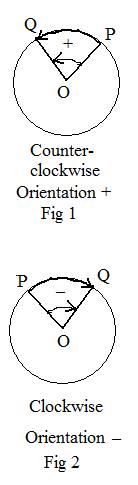
Of course the central angle POQ is positive if and only if the subtended arc has positive orientation. Similarly, the central angle POQ is negative if and only if the subtended arc has negative orientation.
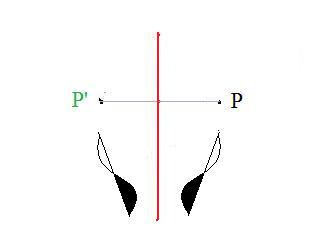 (A) A rectangular piece of paper can be folded in half so that the left edge and right edge coincide. The fold determines a vertical line which divides the paper into two congruent parts. Before folding a point P is made on the paper using ink that dries slowly. The paper is folded and then unfolded. An image point P' is made on the other side of the vertical line. This process can be done repeatedly with points all over on the paper. Then every point has an image point, even points on the line. Their image points coincide with the points themselves. They are fixed points. In the following suppose the points are off of the line.
(A) A rectangular piece of paper can be folded in half so that the left edge and right edge coincide. The fold determines a vertical line which divides the paper into two congruent parts. Before folding a point P is made on the paper using ink that dries slowly. The paper is folded and then unfolded. An image point P' is made on the other side of the vertical line. This process can be done repeatedly with points all over on the paper. Then every point has an image point, even points on the line. Their image points coincide with the points themselves. They are fixed points. In the following suppose the points are off of the line.
(B) There is a definite relation between any point and its image: they are equidistant from the line. More exactly, if a line segment is drawn between any point and its image, the segment is horizontal and the line bisects that segment. Since the line is vertical, it and the segment are perpendicular. Therefore, the line is the perpendicular bisector of the segment. Using this defining feature it is possible to construct by geometry the image point of any given point. If there is a subset of the plane, it too can be reflected about the line. Every point in the subset is reflected about the line to form the image of the subset. This is still true even if the subset crosses the line.
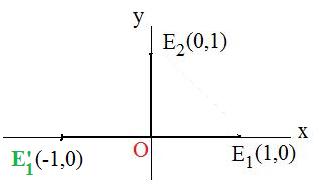 (C) Copy the line and points onto the coordinate plane, so that the line coincides with the y-axis. The special points E1(1,0) and E2(0,1) have images. The image of E1(1,0) is E'1(-1,0) because the y-axis is the perpendicular bisector of the segment E1E'1. The point (0,1) is on the y-axis and therefore (0,1) is its own image.
(C) Copy the line and points onto the coordinate plane, so that the line coincides with the y-axis. The special points E1(1,0) and E2(0,1) have images. The image of E1(1,0) is E'1(-1,0) because the y-axis is the perpendicular bisector of the segment E1E'1. The point (0,1) is on the y-axis and therefore (0,1) is its own image.
(D) The following matrix is obtained from the transposes of the images, namely, (-1,0)t and (0,1)t become columns:
(E) Let L be the linear transformation that carries the special points onto (-1,0) and (1,0). Then
(F) Let P(x,y) and P'(-x,y) be its image. According to (B) it is necessary to show that the y-axis is the perpendicular bisector of the segment PP'. The line segment joining O and E2 lies along the y-axis. It is perpendicular to PP' because the inner product
[3.1a] (Reflection about the y-axis) The linear transformation L defined by
Of course simple observation makes the point (x,y) and its image (-x,y) symmetric about the y-axis. But the above process illustrates a method that will be used for more complicated situations.
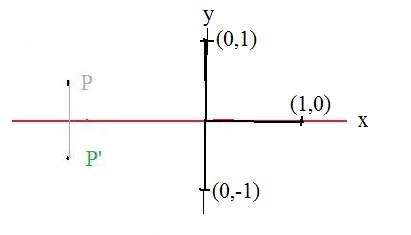 A reflection of a point about a horizontal line is discussed in a similar way. The x-axis is the perpendicular bisector of a vertical line segment joining any point P and its image P'. The images of the special points are (1,0) and (0,-1).
A reflection of a point about a horizontal line is discussed in a similar way. The x-axis is the perpendicular bisector of a vertical line segment joining any point P and its image P'. The images of the special points are (1,0) and (0,-1).
[3.1b] (Reflection about the x-axis) The linear transformation L defined by
As a function the action carries the initial side of an angle onto the initial side of the image angle, and terminal side of an angle onto the terminal side of the image angle. Each angle has an orientation. Reflections about axes reverses the orientation of the right angles. Notice that the reflection about y-axis carries the positive oriented right angle, initial side positive x-axis , terminal side positive y-axis to the negative oriented image angle, initial side negative x-axis, terminal side positive y-axis. Similarly, the reflection about x-axis carries the positive oriented right angle, initial side positive x-axis , terminal side positive y-axis to the negative oriented image angle, initial side positive x-axis, terminal side negative y-axis.
(A) Suppose a point can be "pushed" along a straight line. For any point not on the origin there is a straight line through the given point and the origin. Push the point along this line through the origin. Continue pushing until the point has moved the same distance on the other side of the origin as the given point was on this side of the origin. The origin should be mid-way between the starting place for the point and the ending place. If the point starts on top of the origin, it stays there.
(B) For any point P not on the origin O construct a segment with P as an end point and O is the midpoint of that segment. The other endpoint P' is the image by reflecting P through O If P = O then P is its own image: P' = P.
Only the origin is its own image, the only fixed point of a reflection through the origin.
[3.2a] (Vector description of this reflection) The position vector locating a point, and the position vector locating its image, obtained by a reflection through the origin, are negatives of each other.
Notation: if P' is the image by reflection through the origin of point P then p' = - p
The mid point of segment PP' is located by (1/2) (sum of end points) = (1/2) (p' + p) = (1/2) (-p + p) = (1/2) 0 = 0 which locaters the origin.
(C) It is not difficult to show that the images of the special points (1,0) and (0,1) are (-1,0) and (0,-1).
(D) The matrix obtained from the transposes of these images is
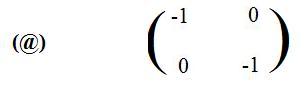
[3.2b] (Reflection through the origin is a linear transformation) The linear transformation L defined by
The mid point of the segment with end points (x,y) and (-x,-y) is (0,0) which is the origin. This justifies [3.1b]
It will be shown later that the reflection through the origin preserves the orientation of any angle with vertex at the origin (the orientations of any such angle and its image are the same.
 (A) A horizontal line is on the paper and the paper stands on the bottom edge. A point is above the line. Suddenly the point is given weight, and the point falls straight down onto the line and becomes the projected image. (All points above the line fall straight down onto the line to become images.) Points below the line float straight up until hitting the line. Any point already on the line is its own image, it is left fixed. All the points have been orthogonally projected onto the horizontal line.
(A) A horizontal line is on the paper and the paper stands on the bottom edge. A point is above the line. Suddenly the point is given weight, and the point falls straight down onto the line and becomes the projected image. (All points above the line fall straight down onto the line to become images.) Points below the line float straight up until hitting the line. Any point already on the line is its own image, it is left fixed. All the points have been orthogonally projected onto the horizontal line.
(B) If the point P is above or below the given horizontal line, construct a line through P perpendicular to the given line. Where this constructed line intersects the horizontal line is a point P' called the orthogonal projection of P upon the horizontal line. If P is a point already on the horizontal line then P is its own image: P' = P.
The segment PP' is perpendicular to the horizontal line. That is why the projection is called "orthogonal."
(C) Place the horizontal line and points on the coordinate plane so that the horizontal line coincides with the x-axis. The vertical projection carries the special points (1,0) and (0,1) onto images (1,0) and (0,0) respectively.
(D) From the transposes of those images the following matrix is formed:
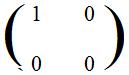
(E)
[3.3a] (The orthogonal projection onto the x-axis is a linear transformation) The linear transformation L defined by
(F) The proof of [3.3a] is simple. The image point (x,0) is on the x axis. If x is not zero, then the segment joining point (x,y) and point (x,0) is vertical, and therefore perpendicular to the x-axis.
The discussion of the orthogonal projection onto the y-axis is similar. However, the projection line from any point off of the y-axis onto the image point on the y-axis is horizontal. The image points of the special points (1,0) and (0,1) are (0,0) and (0,1) respectively. The following matrix is formed from the transposes of those images:
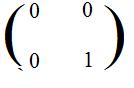
[3.3b] (The orthogonal projection onto the y-axis is a linear transformation) The linear transformation L defined by
There is no discussion of orientation with projections onto lines
Acctually the term rotational function might be a more accurate term for a rotation about the origin. The plane does not move, but points are associated with other points that are a specified number of degrees ahead of them.
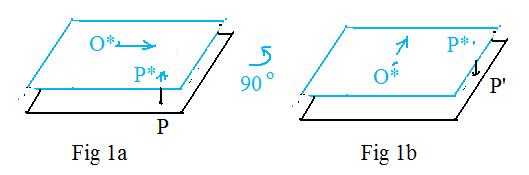 (A3) (Three dimensional description) On an immovable paper is a point O (not shown in Fig 1a).All points on the paper are copied onto another movable paper that lies entirely on top of the immovable paper. Any given point P on the immovable paper is copied upward onto point P* on the movable paper. (O is copied upward onto O*.) The movable paper is then rotated counterclockwise about O* through an angle of 90° . The point P* is copied back down onto the immovable paper, producing the actual (functional) image P' of the given point P (Fig 1b). All the points of the movable paper are copied down onto the immovable paper. The point O* is copied back down onto O (not shown in Fig 1b).
(A3) (Three dimensional description) On an immovable paper is a point O (not shown in Fig 1a).All points on the paper are copied onto another movable paper that lies entirely on top of the immovable paper. Any given point P on the immovable paper is copied upward onto point P* on the movable paper. (O is copied upward onto O*.) The movable paper is then rotated counterclockwise about O* through an angle of 90° . The point P* is copied back down onto the immovable paper, producing the actual (functional) image P' of the given point P (Fig 1b). All the points of the movable paper are copied down onto the immovable paper. The point O* is copied back down onto O (not shown in Fig 1b).
The movable paper is only temporary and is removed from consideration.
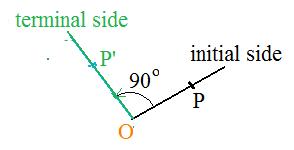
(A2) (Two dimensional description) For any point P not on the origin draw a line through O and P. With its point remaining on O swing the half-line through an angle of 90°. Then it becomes half-line. Point P is carried along by this action and falls on P'. Then P' is the image of P after rotation.
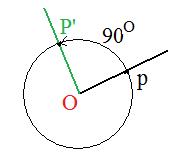
(B) For any point P not on the origin construct a line through O and P. Construct a line through O perpendicular to the line previously constructed. Construct a circle with center at O and radius |OP|.
On the part of the half-line that makes a angle of +90° (and not - 90°) with the previously constructed line locate the intersection of the circle and this half-line. That intersection is the image P' of the given point P.
There are three conditions for P' to be the image of P rotated about O through an angle of 90°:
(1) if P = O then P' = O. (The image of the origin is itself).
(ii) |OP'| = |OP|.
(P' and P are the same distance from the origin)
(iii) angle POP' = 90°. (O and P are different points; the angle is measured counter-clockwise)
For a geometric construction that finds the image P' for a given point P click here.
Copy the fixed paper onto the coordinate plane.
(C) The rotation about the origin through 90° carries the special points (1,0) and (0,1) onto images (0,1) and (-1,0) respectively.
(D) From the transposes of those images form the matrix
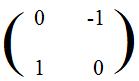
(E) [3.4a] (Rotation through 90° is a linear transformation) The linear transformation L defined by
(i) L(0,0) = (-0,0) = (0,0).
In the following let P be the point (x,y) and P' the image point L(x,y) = (-y,x). Then OP and OP' are position vectors to these points.
(ii) Working with lengths2, |OP'|2 = (-y)2 + x2 = y2 + x2 = x2 + y2 = |OP|2.
(iii) The inner product
OP * OP' = (x,y) * (-y,x) = - xy + xy = 0
Therefore OP and OP' are perpendicular vectors. Hence angle POP' = 90°.
Rotation about the origin preserves orientation of the right angles. Notice that the rotation carries the positive oriented right angle, initial side positive x-axis , terminal side positive y-axis to the positive oriented image angle, initial side positive y-axis, terminal side negative x-axis.
(B) For any point P let P' be the image of P made by the completed action.
(i) If P = O then P' = O.
(ii) There is a positive real number λ such that vectors
The number λ is called the coefficient of the similitude. It is always a positive real number and is equal to a ratio of distances:
(C) The special points (1,0) and (0,1) are carried onto points (λ,0) and (0,λ).
(D) The transposes of these images determine the matrix
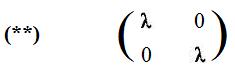
(E)
[3.5a] (Similitudes are linear transformations) The linear transformation defined by
(F) Let P and P' be the points with labels (x,y) and (λx, λy) respectively. Then OP' = (λx, λy) = λ(x,y) = λOP.
[3.5b] (Parallel image) A similitude carries segments onto parallel segments.
Notation: If P' and Q' are images of points P and Q respectively, then segment P'Q' is parallel to segment PQ.
Vectors OP' = λOP and OQ' = λOQ. Converting these vectors to position vectors
[3.5c] (Preserving angles) A similitude carries intersecting lines onto intersecting lines in such a way that the angle of intersection of the second pair of lines is congruent to the angle of intersection of the first pair.
Notation: If points A', B', C' are images of points A, B, C then angle A'B'C' is congruent to angle ABC.
By [3.5b] segment A'B' and B'C' are parallel to AB and BC respectively. Therefore angle A'B'C' is congruent to angle ABC.
(A) The folding of the paper discussed in [3.1] cam be done diagonally to make the image of a point.
(B)
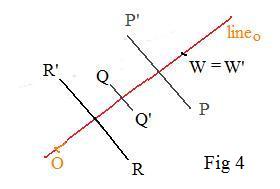
The geometric description of an orthogonal reflection about any line is the same outside the coordinate plane. In the adjacent figure a slant lineo is used. It is called the axis of the reflection. Points P,Q,R are reflected about lineo onto points P',Q',R'. Again the axis is the perpendicular bisector of segments PP', QQ', RR'. Point W is on the axis, so W' = W. If a lintr is to be involved, then the axis must pass through the origin O. Incidentally, the word "orthogonal" means perpendicular. There are reflections, not discussed in these sections, of "slant reflections" in which the segments PP'.QQ', RR' are not perpendicular to the axis. Their mid points do lie on the axis, and all the segments are parallel. Only orthogonal reflections are discussed here. Sometimes the word "orthogonal" is omitted, but understood.
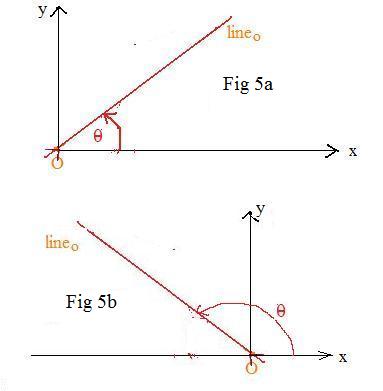 It is obvious that the position and location of the axis completely determines the reflection. The axis may be placed as a lineo in the coordinate plane so that it passes through the origin O. Let θ be the inclination angle as shown. If θ is between 0° and 90° then lineo slants from lower left to upper right (Fig 4a). If lineo is between 90° and 180° then lineo slants from lower right to upper left (Fig 4b). There is no need to consider angles between 180° and 360° because θ and θ - 180° determine the same lineo.
However, similitudes do not preserve lengths of segments. Segments and their images are not necessarily congruent.
It is obvious that the position and location of the axis completely determines the reflection. The axis may be placed as a lineo in the coordinate plane so that it passes through the origin O. Let θ be the inclination angle as shown. If θ is between 0° and 90° then lineo slants from lower left to upper right (Fig 4a). If lineo is between 90° and 180° then lineo slants from lower right to upper left (Fig 4b). There is no need to consider angles between 180° and 360° because θ and θ - 180° determine the same lineo.
However, similitudes do not preserve lengths of segments. Segments and their images are not necessarily congruent.
Using the plan of six steps (A) --- (F) it is possible to derive legimately the formula
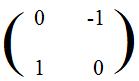
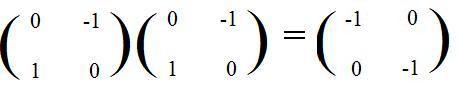
[3.6b] The linear transformation L defined by
The formula and associated matrix in [3.6b] are identical to a formula and associated matrix in [3.2b]. This proves:
[3.6c] (Equivalence of a rotation and a reflection) A reflection through the origin and a rotation about the origin through 180° are equivalent actions.
(A3) (Three dimensional description) This description is almost identical to (A3) in subsection [3.4], except the movable paper is rotated through a given angle, instead of 90°.
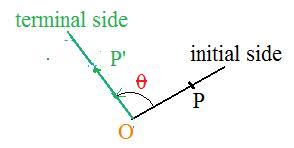 (A2) (Two dimensional description) This description is almost identical to (A2) in subsection [3.4], except the half line is rotated through a given angle θ instead of 90°.
(A2) (Two dimensional description) This description is almost identical to (A2) in subsection [3.4], except the half line is rotated through a given angle θ instead of 90°.
(B) There are three conditions for P' to be the image of P rotated about O through an angle θ
(1) if P = O then P' = O. (The image of the origin is itself).
(ii) |OP'| = |OP|.
(P' and P are the same distance from the origin)
(iii) angle POP' = θ. (the angle is measured counter-clockwise if θ is positive, and clockwise if θ is negative)
(C) If point E1(1,0) is rotated through angle θ to produce image point E'1 then by definition of cosine and sine E'1 has the coordinates (cos θ, sin θ):
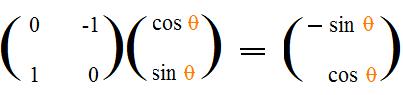
(D) The transposes of the images given in the above paragraph produce the matrix

(F)
(i) L leaves the origin fixed because L(0,0) = (0 -- 0, 0 + 0) = (0,0).
(ii)points L(x,y) and (x,y) are the same distance from the origin because
|L(x,y)|2 = (x cos theta; -- y sin θ)2 + (x sin θ + y cos &theeta;)2;
x2 cos2 θ -- 2xy cos θ sin θ + y2 sin2 θ
+ x2 sin2 θ + 2xy sin &theeta; cos θ + y2cos2 θ
= x2(cos2 θ + sin2 θ)
= x2 + y2
= |(x,y)|2
Therefore,
(iii) It is possible to use Lemma2 to prove that L preserves angles with vertices at the origin. However, the proof below uses the inner product.
The angle of rotation is θ that is given in the formula for L. It is the angle between the positive x-axis and the segment joining the origin to the point L(1,0) = (cos θ, sin θ) which is the inner product L(1,0)*(1,0) = cos θ It is necessary to show that θ is also the angle between segments joining the origin to (x,y) and L(x,y).
L(x,y) * (x,y) = (x cos *theta; -- y sin θ, x sin θ + y cos θ) * (x,y)
x2 cos θ -- xysin θ + xy sin θ + y2 cos θ
(x2 y2) cos θ
|L(x,y)| |(x,y)| cos θ
Therefore,
(A) The folding of the paper discussed in [3.1A] can be done slantwise. Then points will be copied orthogonally across the fold as a reflection.
(B)
 The geometric description of an orthogonal reflection about any line is the same outside the coordinate plane. In the adjacent figure a slant lineo is used. It is called the axis of the reflection. Points P,Q,R are reflected about lineo onto points P',Q',R'. Again the axis is the perpendicular bisector of segments PP', QQ', RR'. Point W is on the axis, so W' = W. If a lintr is to be involved, then the axis must pass through the origin O. Incidentally, the word "orthogonal" means perpendicular. There are reflections, not discussed in these sections, of "slant reflections" in which the segments PP'.QQ', RR' are not perpendicular to the axis. Their mid points do lie on the axis, and all the segments are parallel. Only orthogonal reflections are discussed here. Sometimes the word "orthogonal" is omitted, but understood.
The geometric description of an orthogonal reflection about any line is the same outside the coordinate plane. In the adjacent figure a slant lineo is used. It is called the axis of the reflection. Points P,Q,R are reflected about lineo onto points P',Q',R'. Again the axis is the perpendicular bisector of segments PP', QQ', RR'. Point W is on the axis, so W' = W. If a lintr is to be involved, then the axis must pass through the origin O. Incidentally, the word "orthogonal" means perpendicular. There are reflections, not discussed in these sections, of "slant reflections" in which the segments PP'.QQ', RR' are not perpendicular to the axis. Their mid points do lie on the axis, and all the segments are parallel. Only orthogonal reflections are discussed here. Sometimes the word "orthogonal" is omitted, but understood.
 It is obvious that the position and location of the axis completely determines the reflection. The axis may be placed as a lineo in the coordinate plane so that it passes through the origin O. Let θ be the inclination angle as shown. If θ is between 0° and 90° then lineo slants from lower left to upper right (Fig 4a). If lineo is between 90° and 180° then lineo slants from lower right to upper left (Fig 4b). There is no need to consider angles between 180° and 360° because θ and θ - 180° determine the same lineo.
It is obvious that the position and location of the axis completely determines the reflection. The axis may be placed as a lineo in the coordinate plane so that it passes through the origin O. Let θ be the inclination angle as shown. If θ is between 0° and 90° then lineo slants from lower left to upper right (Fig 4a). If lineo is between 90° and 180° then lineo slants from lower right to upper left (Fig 4b). There is no need to consider angles between 180° and 360° because θ and θ - 180° determine the same lineo.
(C) It is possible to produce an geometric argument that a reflection about the line with inclination angle θ carries (1,0) and (0,1) onto the points
The reader can click here to see that geometric argument supporting this statement. However there is another shorter discussion supporting this statement. It starts with an observation that a rotation about the origin through angle 2θ carries the same special points (1,0) and (0,1) onto