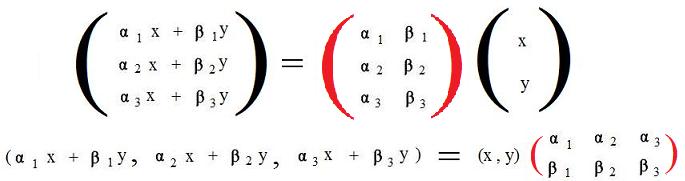
It is easily verified that the images of the special arrays (1,0) and (0,1) for this linear transformation are
The reader can easily verify the following two identities:
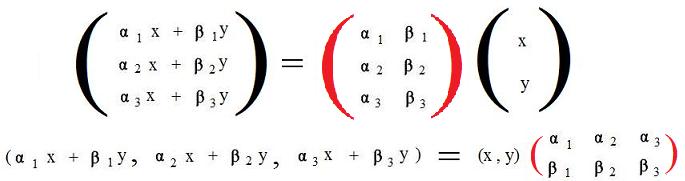
Let M = 3x2 matrix in the top identity. Then the transpose M' = 2x3 matrix in the bottom identity. It could be said that M is the matrix obtained direcctly from the (coefficients of) the arrays, but M' is obtained from images of the special arrays. Using the definition of F, F(x,y) = (x,y)M' . (Equations such as this motivate some algebraist to rearrange the notation of a function to (x,y)F.) This arrangement is more compatible with the usual function notation, since F carries horizontal arrays onto horizontal arrays.
[2.x] (Composition and product) Let F be a linear transformation from a first linear objecct into a second linear object, and let G be a linear transformation from the second linear object into a third linear object. If M' is the matrix corresponding to F and N' is the matrix corresponding to G, then the matrix corresponding to the composition GF is the matrix product M'N'.