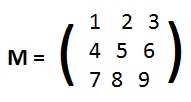
In words, L carries the sum of two points onto the sum of their images. L carries the product of a real number and a point onto the product of that real number and the image of the point.
Recall that arrays may be added and multiplied by a real number λ:
(a) (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2);
(b) λ(x,y) = (λx, λy)
Basic to the proof is the 2x2 matrix M associated with L. In a prevfious chapter there was a discussion about a distributive law for matrices.
L(x1, y1) + L(x2, y2) =
(x1, y1)M + L(x2, y2)M =
(x1 + x2, y1 + y2)M =
L( (x1 + x2, y1 + y2) ).
L( λ(x,y) ) = L(λx,λy) = (λx, λy)M = λ(x,y)M = λL(x,y).
[1.5] A function L on a vector space is a linear transformation if and only if it has the following two properties, for all elements u and v in the vector space, and any real number λ:
(a) L(u + v) = L(u) + L(v);
(b) L(λv) = λL(v)
Consider the collection of all polynomials in x with real numbers as coefficients. The collection has all the properties of a vector space, including addition of polynomials and products with real numbers. The derivative operator d/dx is a function that carries each polynomial onto another polynomial (the derivative). For example, d/dx (x2 + 4x +5) = 2x + 4.
Let p(x) and q(x) represent any polynomials in x with real number coefficients. By the rules of differentiation:
(a) d/dx ( p(x) + q(x) ) = d/dx p(x) + d/dx q(x).
(b) d/dx λp(x) = λ d/dx p(x).
Here u = p(x), v = q(x) in (a),
v = p(x) in (b) and
L = d/dx.
[1.5] (Defining properties of a linear transformation) A function L on a vector space is a linear transformation if and only if it has the following two properties, for all elements p and q in the vector space, and any real number λ:
(a) L(p + q) = L(p) + L(q);
(b) L(λp) = λL(p);
where u,v have been replaced by p,q.
Recall that vector addition is pictured as a parallelogram. P and Q are arbitrary points in the coordinate plane located by the position vectors p and q. Together with origin O they form three vertices of a parallelogram. To locate the fourth point R, construct and arc at P with radius |OQ| and an arc at Q with radius |OP|. Where the arcs intersect is point R. Therefore, for position vectors p,q,r
Do a very similar construction with the three points L(P),O, L(Q) with intersecting arcs intersecting at a point R'. Therefore,
Example: if L(1,0,0) = (1,2,3), L(0,1,0) = (4,5,6) and L(0,0,1) = (7,8,9) then the matrix associated with L is
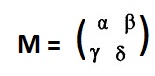 Let L be a linear transformation and M its non-singular associated matrix (see adjacent figure). Since
Let L be a linear transformation and M its non-singular associated matrix (see adjacent figure). Since Let (x1, y1) and (x2, y2) be any points. "Distinct points carried onto distinct points" can be translated as an implication
Starting the chain with the hypotheses in (**) above:
L(x1, y1) = L(x2, y2)
=>
(αx1 + γy1, βx1 + δy1) =
(αx2 + γy2, βx2 + δy2)
=>
(αx1 + γy1, βx1 + δy1) −
(αx2 + γy2, βx2 + δy2)
= (0,0)
=>
(αx1 − αx2 + γy1 − γy2,
βx1 − βx2 +δy1 − δy2)
= (0,0)
=>
(α(x1 − x2) + γ(y1 − y2),
β(x1 − x2) + δ(y1 − y2))
= (0,0)
=>
(αx + γy, βx + δy) = (0,0)
=>
αx + γy = 0
αx + γy = 0
βx + δy = 0
βx + δy = 0
=>
[multiply left top equation by δ and left bottom equation by γ and subtract to get]
(αδ − βγ)x = 0.
multiply right top equation by β and right bottom equation by α and subtract to get]
(αδ − βγ)y = 0.
But (*) forces x=0 and y=0.
Then (***) forces x1= x2 and y1= y2.
This proves (**).