Return to main text in Chapter 1
Additional Material D2 - YYYD2
(*) Mid point array) The the sum of the two arrays that locate the end points of a segment is twice the array that locates the mid point of the segment.
Notation: If array1 and array2 locate the end points of a line segment and if array3 locates the mid point, then
(#)
2 array3 = array1 + array2
From graphs in elementary algebra, the mid point formulas for array3 are:
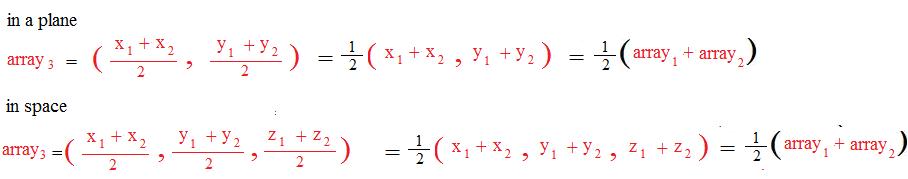
Multiplying all expressions by 2 produces the desired equation (#) above for plane and space.
Coincidence of sums of position vectors and arrays
[3.12] (Corresponding sums) If two position vectors and two arrays locate the same two points respectively, then the sum of the position vectors and the sum of the arrays locate the same point.
Notation: if both p and array1 locate point P, and both q and array2 locate point Q, then their sums
p + q and array1 + array2
locate the same point.
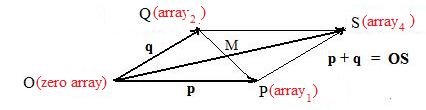 Recall that O is the name of the origin, and it is located by the zero array = (0,0) or the <zero array = (0,0,0).
Construct the addition parallelogram for the vector sum p + q which is shown in the adjacent figure as parallelogram OPSQ. Diagonal vector OS = p + q. Assign array1
to point P and array2 to point Q. Assign array4 to point S. Needed to show is
Recall that O is the name of the origin, and it is located by the zero array = (0,0) or the <zero array = (0,0,0).
Construct the addition parallelogram for the vector sum p + q which is shown in the adjacent figure as parallelogram OPSQ. Diagonal vector OS = p + q. Assign array1
to point P and array2 to point Q. Assign array4 to point S. Needed to show is
array4 =
array1 + array2.
A theorem in plane geometry says that the diagonals of a parallelogram bisect each other. In the figure, M is the midpoint on both diagonals OS and PQ. Therefore, by the discussion about midpoints above, both the sums
array1 + array2 and zero array + array4
are equal to twice the array that locates the mid point M. Therefore, the two sums are equal:
array1 + array2 = zero array + array4. But the zero array is the additive identity, so it can be "erased" and the result is the desired equality:
array4 =
array1 + array2.
This argument shows that the sums p + q and array1 + array2 locate the same point, namely S.
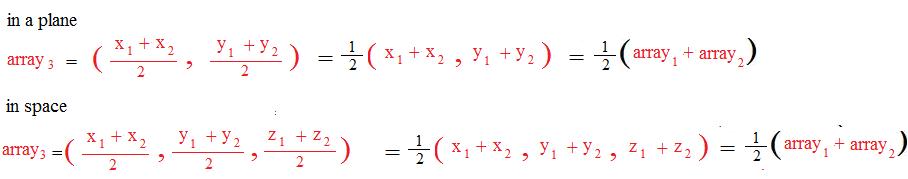
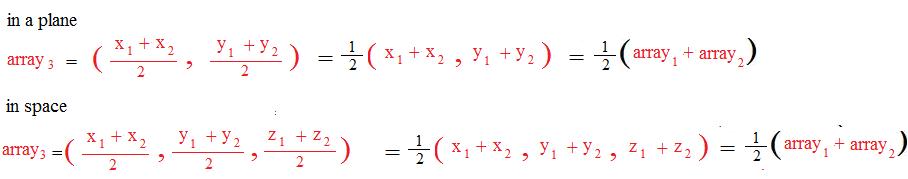
 Recall that O is the name of the origin, and it is located by the zero array = (0,0) or the <zero array = (0,0,0).
Construct the addition parallelogram for the vector sum p + q which is shown in the adjacent figure as parallelogram OPSQ. Diagonal vector OS = p + q. Assign array1
to point P and array2 to point Q. Assign array4 to point S. Needed to show is
Recall that O is the name of the origin, and it is located by the zero array = (0,0) or the <zero array = (0,0,0).
Construct the addition parallelogram for the vector sum p + q which is shown in the adjacent figure as parallelogram OPSQ. Diagonal vector OS = p + q. Assign array1
to point P and array2 to point Q. Assign array4 to point S. Needed to show is