Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer Programs
Return to index of all chapters in this volume
Volume C Chapter 1
Relations
For a special way of "joining" sets to produce coordinate expressions like (a,b,c,d,e) click here
Section 1: Relations between a pair of sets
The idea of relations exist among people. A father and his son have a relation, a brother and brother is a relation. And of course some people have no relation to each other. In any case two people may or may not have a relation..
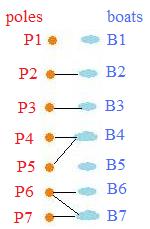 The idea of a relation can be extended to objects. The following is an example.
Seven boats are tied up at a dock where there are seven poles. The adjacent figure shows how they are tied to the poles. One pole has nothing tied to it. Two boats are not tied to any poles (anchors are used instead). Two boats are so big that they must be tied to two poles. The poles and boats receive labels as shown, to form sets:
The idea of a relation can be extended to objects. The following is an example.
Seven boats are tied up at a dock where there are seven poles. The adjacent figure shows how they are tied to the poles. One pole has nothing tied to it. Two boats are not tied to any poles (anchors are used instead). Two boats are so big that they must be tied to two poles. The poles and boats receive labels as shown, to form sets:
Poles = {P1, P2, P3, P4, P5, P6, P7} and Boats = {B1, B2, B3, B4, B5, B6, B7}.
Let poles and boats be related if they are tied together. More formally,
pole x ~ boat y if and only if pole x is tied to boat y.
This introduces a new symbol ~ (tilda). It will be used to mean "is related to". But sometimes the ordered pair (x,y) will be used to mean x ~ y.
The statement that two objects are related is a logical statement. It may be true or false. P5 ~ B4 is true. But P2 ~ B6 is false. Every relation has a truth set. The open statement x ~ y produces the following 7x7 truth table:
(*)
B1 B2 B3 B4 B5 B6 B7
P1 F F F F F F F
P2 F T F F F F F
P3 F F T F F F F
P4 F F F T F F F
P5 F F F T F F F
P6 F F F F F T T
P7 F F F F F F T
The truth set
{(P2,B2), (P3,B3),
(P4,B4), (P5,B4),
(P6,B6), (P6,B7),
(P7,B7)}
reveals what poles and what boats are tied together.
The reverse of a relation x ~ y is the relation y ~ x. In the previous example boats and poles would be interchanged and the relation would be
boat y is tied to pole x
Being tied is a mutual relation. If a pole is tied to a boat then that same boat is tied to that same pole. A symmetry exists. But there are relations without symmetry.
For example, a father - son relation.
[1.1] (Symmetric relations) A relation is symmetrical if every relation and its reverse have the same truth value.
Notation: Relation ~ between sets U and V is symmetrical if and only if for all x in U and for all y in V, x ~ y iff y ~ x.
Section 2: Equivalence relations
Veryt useful are relations on the same universe, that is, a relation between a universe U and itself. There, a special type of relation is very important and found in many parts of mathematics.
[2.1] (Equivalence relations) A relation ~ on a universe U is an equivalence relation if and only if it has the following three properties:
(a) the relation is reflexive (every object in U is equivalent to itself): for all x in U, x ~ x;
(b) the relation is symmetrical: for all x,y in U, if x ~ y then y ~ x;
(c) the relation is transitive: for all x,y,z in U, if x ~ y and y ~ z then x ~ z.
Symmetry is best noticed if the relation is expressed as coordinates of ordered pairs: if (x,y) then (y,x). In analytic geometry the points (x,y) and (y,x) are symmetric about the line y=x.
Example [2.1a]
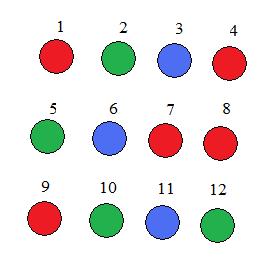 Example
Example
Twelve colored balls are displayed as shown in the adjacent figure. It is easily shown that the relation
x ~ y if and only if x and y have the same color
has all three properties of an equivalence relation:
reflexive: ball x ~ ball x because ball x has the same color as itself;
symmetric: if ball x ~ ball y then ball y ~ ball x: because if balls x and y have the same color then balls y and x have the same color;
transitive: if ball x ~ ball y and ball y ~ ball z then ball x ~ ball z: if ball x and ball y have the same color, and ball y and ball z have the same color then all three have the same color, so ball x and ball z have the same color.
It is possible to collect balls of the same color into three subsets:
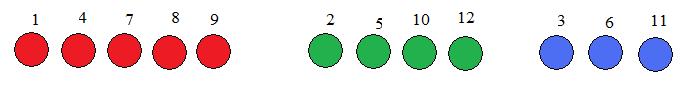
In the figure each of the balls has been assigned, as a name, a number in the set
N12 = {1,2,3,4,5,6,7,8,9,10,11,12}
Then the following are among the true relations:
4 ~ 9, 5 ~ 10, 6 ~ 11
Using the numbers it is possible to construct a 12x12 truth table for this relation.
The above subsets of balls of the same colors determine the following subsets of N12:
R={1,4,7,8,9}, G={2,5,10,12}, B={3,6,11}
Recall that a partition is a collection (family) of disjoint subsets whose union is all of the universe. These three subsets form a partition {R,G,B} of N12.
Then the original relation among balls is equivalent to saying among numbers that
for all x,y in N12, x ~ y if and only if both x and y are in the same subset of the partition.
Example [2.1b]
In the previous example the balls were colored in some random way. In the following universe U the colors red, green, blue, brown are made in an orderly manner (every fourth ball has the same color):
U = {
0, 1, 2, 3,
4, 5, 6, 7,
8, 9, 10, 11,
12, 13, 14, 15,
16, 17, 18, 19
}
The numbers are names of colored balls (not shown). The color of the balls has been transferred to the numbers. The relation is
for all x,y in U, x ~ y if and only if x and y have the same color
Collecting the balls of the same colors the obvious partition of U is {R,G,B,W} where
R={0, 4,, 8, 12, 16},
G={1, 5, 9, 13, 17},
B={2, 6, 10, 14,
18}
W={3, 7, 11, 15, 19,}
Actually colors are not needed. Replace U by J20, the integers mod 20 (without colors). Notice that for any two numbers in one of the subsets of the partition their difference is divisible by 4. Therefore, the relation on J20 is
for all x,y in J20, x ~ y if and only if the difference x - y is divisible by 4
This relation produces partition {R,G,B,W} of J20 without involving any colors.
More examples of equivalent relations on different universes can be given. Every time a partition of the universe is produced. A special notation is developed for the subsets of the partitions produced by equivalent relations:
for any object b in universe U, [b] = subset of all objects in U to which b is (truly) related.
Notation: x is in [b] if and only if b ~ x
[b] is called the equivalence class containing x. The subsets R,G,B,W are equivalence classed induced by the relation ~.
In the previous example where the universe is J20,
[0] = R, [1] = G, [2] = B, [3] = W, [10] = B, [15] = W
Therefore [2] = [10] and [3] = [15].
Every number is in some equivalence class (because the relation is reflexive). The equivalence classes
(**) [0], [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19]
are not all different because
[0] = [4] = [8] = [12] = [16] = R, [1] = [5] = [9] = [13] = [17] = G, [2] = [6] = [10] = [14] = [18] = B, [3] = [7] = [11] = [15] = [19] = W
This also shows that each of the subsets R,G,B,W appears five times in the listing (**).
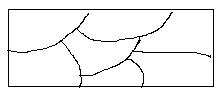 If there is already a partition of a universe into subsets then an equivalence relation can be derived from it. In the adjacent figure the universe U is the interior of the rectangle. The curves show how that interior is divided up into pieces (subsets), forming a partition of U. The induced relation ~ is defined as follows
If there is already a partition of a universe into subsets then an equivalence relation can be derived from it. In the adjacent figure the universe U is the interior of the rectangle. The curves show how that interior is divided up into pieces (subsets), forming a partition of U. The induced relation ~ is defined as follows
for all x,y in U, x ~ y x and y belong to the same subset of the partition
It is trivial to verify each of the three conditions of [2.1] for an equivalence relation.
[2.2] (Partition inducing a relation) Any partition of a universe induces an equivalence relation on the universe.
Notation: for all x,y in U, x ~ y x and y belong to the same subset of the partition
The examples [2.1a] and [2.1b] indicate the truth of the following:
[2.3] (A relation induces a partition) An equivalence relation on a universe induces a partition of that universe: the equivalence class of each object in the universe produces a subset of the partition.
Notation: The family of all equivalence classes [x] of all the objects x form a partition of the universe.
Given: an equivalence relation ~ on a universe U. Then
(a) all the equivalence classes cover U. Since ~ is reflexive, then x ~ x and this implies x is iin [x] by definition of equivalence class. Therefore, every object in U is in some equivalence class.
(b) The equivalence classes are disjoint. This is equivalent to saying that for any two objects b,c [b] = [c] or that the intersection [b] /\ [c] is empty. The equality is trivial if b = c. Suppose b and c are different.
Consider the intersection [b] /\ [c]. If it is empty then the argument is finished. Suppose the intersection is not empty.
Let d be some object in the intersection. Then d is is [b] and d is in [c].
By definition of d being in an equivalence classes [b] and [c], b ~ d and c ~ d. By symmetry this means that b ~ d d ~ c. From the transitive law, b ~ c. This means that [b] = [c].
To show this, let w be any object in [b]. Then b ~ w. By symmetry w ~ b. But b ~ c so by transitivity w ~ c and then c ~ w. So w is in [c]. This makes [b] a subset of [c].
A similar argument of t in [c] => t in [b] shows that [c] is a subset of [b].
Therefore [b] and [c] are subsets of each other. This means that [b] = [c].
Therefore, [2.2] and [2.3] together imply that establishing an equivalence relation on a universe is equivalent to establishing a partition of that same universe.
 The idea of a relation can be extended to objects. The following is an example.
Seven boats are tied up at a dock where there are seven poles. The adjacent figure shows how they are tied to the poles. One pole has nothing tied to it. Two boats are not tied to any poles (anchors are used instead). Two boats are so big that they must be tied to two poles. The poles and boats receive labels as shown, to form sets:
The idea of a relation can be extended to objects. The following is an example.
Seven boats are tied up at a dock where there are seven poles. The adjacent figure shows how they are tied to the poles. One pole has nothing tied to it. Two boats are not tied to any poles (anchors are used instead). Two boats are so big that they must be tied to two poles. The poles and boats receive labels as shown, to form sets:
 Example
Example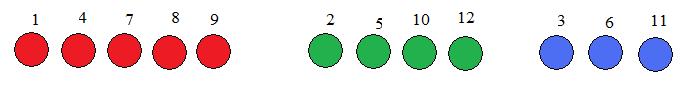
 If there is already a partition of a universe into subsets then an equivalence relation can be derived from it. In the adjacent figure the universe U is the interior of the rectangle. The curves show how that interior is divided up into pieces (subsets), forming a partition of U. The induced relation ~ is defined as follows
If there is already a partition of a universe into subsets then an equivalence relation can be derived from it. In the adjacent figure the universe U is the interior of the rectangle. The curves show how that interior is divided up into pieces (subsets), forming a partition of U. The induced relation ~ is defined as follows