Section 4  Transformations and Fixed Points

A function carries elements from a first set to a second set. In this section the second set is equal to the first set.

[4.1a] A transformation on a set is a function that carries elements of that set back onto elements in that same set.

Another way of saying the same thing is:

[4.1b] A transformation is a function whose range is contained in its domain.

Often the capital letters S and T are used as names of transformations in these discussions. Sometimes R is used when there is no confusion between transformations and the set of real numbers. Sometimes F and L are used. The capital letter I still denotes the identity transformation. It carries each element onto itself.

These conventions are not observed in other textbooks, especially with linear transformations. Linear transformations are discussed in detail in another volume.

[4.2] The following are four transformations I,F,S,T defined on the set {a,b,c,d} of four distinct elements:

I                  F                S                T
a --> a        a --> d         a --> c        a --> b
b --> b        b --> a        b --> c        b --> d
c --> c        c --> c        c --> b        c --> c
d --> d        d --> b        d --> d        d --> a

[4.3] The following are four (new) transformations I,F,S,T defined on the set of all real numbers.

I                  F                  S                T
x --> x        x --> x2         x --> x3        x --> 2x
where x runs through all the real numbers.



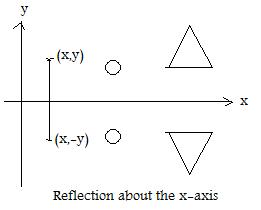
[4.4] Many important transformations on the coordinate plane have a geometric character. The transformation (x,y) --> (x,-y) carries points above the x-axis onto points below the x-axis. At the same time, it carries points below to points above. A circle above the x-axis is carried onto a congruent circle below. Similarly for line segments, triangles, parallelograms,...etc. In fact, everything below the x-axis is a mirror image of what is above the x-axis. This transformation is called a reflection of the plane about a line.)





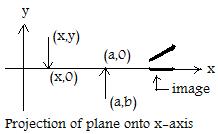
[4.5] Another common geometric transformation is the projection of a plane onto a line in that plane. In the adjacent figure, the transformation (x,y) --> (x,0) projects the plane onto the x-axis. Intuitively speaking, this transformation collapses the plane onto a line in that plane.

Click here for more discussions of trensformations in geometry.


Consider two transformations on the same set: S and T. Let x be any element in the set. Then S carries that element back into the set. Let y be the image. Now T carries y onto some element in the set. Call that image z. The process of computing the product of the two transformations can be indicated in the following "chain of arrows" notation:

S     T 
x --> y -->z
This notation is naturally read from left to right, indicating that S acts first. Up until now the notation f(x) has been used to denote a function f acting on an element x. There was the awkward situation of reading backward the product gf(x), where f acts first on element x. In this section the element part x will be written before the name of the transformation: S:  (x)S. In (x)ST the transformation S acts on x first, then T acts on the result (x)S:
x --> (x)S --> (x)ST

For example, using S and T as defined in [4.2], the computation of the product  ST   can be shown in two notations:

S      T                                                 ST
c --> b --> d        (c)ST = (b)T = d        c --> d
b --> c --> c        (b)ST = (c)T = c        b --> c
c --> b --> d        (c)ST = (b)T = d        c --> d
d --> d --> a        (d)ST = (d)T = a        d --> a
Both show that transformation S acts first.

The next three statements indicate the algebraic properties of transformations. For positive real numbers, it is possible to multiply them, the product of any three can be accomplished by combining any two with the third, and 1 is the multiplicative identity: 1x = x.

[4.6] Closure The product of any two transformations on a set is a transformation on that same set.

Let x be any element of a set on which S and T are transformations. Then (x)S is a element of that same set. Then (x)ST is an element of that same set. Therefore, ST carries elements of the set back into the same set.

The transformations in [4.6] may be the same. Let T be a transformation, then T2 = TT,   T3 = TTT etc. Define T1 = T and T° = I. This will allow addition of exponents.

[4.7] Associative For any three transformations F,S,T on the same set, (FS)T = F(ST).

The associative law is true for any (conformable) functions, as mentioned in a previous section. This theorem means that in computing the product of any three transformations any two can be computed first and then the third, as long as the order of them is the same.

It also means that T3 = T2T    T3 = TT2.

[4.8] Identity On any set there is an identity transformation I.
(x)I = x for all x. I carries each element back onto itself.

[4.9] Inverses In the collection of all non-singular transformations on a set, every transformation there has an inverse.

The properties of transformations given by [4.6], [4.7], [4.8],[4.9] reveal the algebraic nature of them. In fact in modern algebra such a collection is called a semi-group. But without the property of all transformations having inverses (i.e. being non-singular) they do not form a group.

If x is a real number not zero then its reciprocal 1/x exists and is itself a real number. The product of the two is 1. (1 is called the multiplicative identity.) The number 1/x is the inverse of x. 1/4 is the inverse of 4, because their product is 1. -3/2 is the inverse of -2/3 because their product is 1. More generally, whatever fits in ( ) and satisfies x( ) = 1 is the inverse of x. Notice the problem if x=0: nothing put in ( ) satisfies 0( ) = 1 because the product of zero and any number is zero, never 1. There is a number that has no inverse.

A similar situation exists with all the transformations on a set. Some transformations do not have an inverse transformation. The inverse transformation does not exist. Such transformations are singular. They are not one-to-one correspondences. Either they are not one-to-one or not "onto" or both. For example, in [4.2] the transformation S is not one-to-one, because it carries distinct elements a and b onto the same element, namely c. S is not "onto" because the element a is not an image of anything.

The collection of all non-singular transformations on a set has closure (product), the identity transformation is non-singular, and by definition every non-singular transformation has an inverse. This collection forms a group. Groups are discussed in more detail in another volume.

Intuitively speaking, a transformation on a set "picks up" all the elements in that set and "puts" them back into the set. For non-singular transformations, the action is reversable. Every element is carried back onto the original element by the inverse transformation.

While a transformation "picks" up all the elements of a set and puts them back into the set, some element may be put back onto its own image . This is equivalent to saying that the transformation leaves that element fixed. There may be more than one element left fixed. For example, the transformation T in [4.2] leaves the element c fixed, but S leaves no element fixed. All three functions I,F,S leave the real number 1 fixed. I and S there leave -1 fixed. T moves everything and leaves nothing fixed. On any set the identity transformation I leaves every element fixed.

[4.10] If a transformation on some set carrries an element back onto itself, that element is called a fixed point of the transformation.

If (w)T = w then w is a fixed point of T.

In [4.4] and [4.5] only points on the horizontal x-axis are fixed points of the reflection and of the projection. The x-axis is the set of all fixed points.

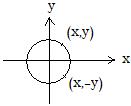The adjacent figure shows again the reflection F about the x-axis: (x,y)F = (x,-y). The circle x2 + y2 = 25 has center at the origin. Since x2 + (-y)2 = 25 is also a point on the circle and also the image of the point (x,y), F carries all points on the circle back into the circle. Yet only (-5,0) and (5,0) are fixed points that are on the circle.

There may be more than one fixed point. Some or all of these points may be collected into a subset.

[4.11a] A transformation leaves a subset fixed pointwise if every element of the subset is left fixed.

The following transformation T on P7 leaves each of the integers 2,4,5,7 fixed:

(1)T=5, (2)T=2, (3)T=3, (4)T=4, (5)T=5, (6)T=2, (7)T=7
Therefore the following subsets are left fixed pointwise:
{2,4,5,7}, {4,5,7}, {2,5}, {5}
plus 11 more proper non-empty subsets of {2,4,5,7}. Usually the subset of all fixed points is the most important.

By its definition the identity transformation on a set is the only transformation that leaves the entire set fixed pointwise.

[4.11b] A transformation leaves a subset fixed setwise if it carries the subset back onto itself.

Let S be a transformation on P7 defined by:

(1)S=5, (2)S=5, (3)S=6, (4)S=7, (5)S=4, (6)S=1, (7)S=2
The subset {2,4,5,7} is left fixed setwise. ({2,4,5,7})S={7,5,2,4}. Obviously, the transformation S carries the subset {2,4,5,7} back onto itself.

However, it is quite possible that a transformation leaves a subset fixed setwise, and that subset contains some fixed points. In fact, if a transformation leaves a subset fixed pointwise, that transformation also leaves that subset fixed setwise.

In this section on transformations on a sets there was no restriction on transformations nor on the size of the set except that it be non-empty. However, in the next section the transformations will be one-to-one correspondences and the sets will be finite.