 It is quite possible that only one set be involved with a function. The only way that this can happen is that images of all the elements be back in the same set. This motivates the following definition..
It is quite possible that only one set be involved with a function. The only way that this can happen is that images of all the elements be back in the same set. This motivates the following definition..
Transformations are a very usefool tool throughout mathematics. The reader may notice that this section is much longer than many of the other sections only to give some of this information.. In fact it continues into the next section 5.
 It is quite possible that only one set be involved with a function. The only way that this can happen is that images of all the elements be back in the same set. This motivates the following definition..
It is quite possible that only one set be involved with a function. The only way that this can happen is that images of all the elements be back in the same set. This motivates the following definition..
[4.1] A transformation on a set is a function whose range is contained in that set.
To the right is a figure showing an intuitive idea of a transformation. T sends elements of a set (domain) onto a subset (range).
Often the capital letters S and T are used as transformations in these discussions. Sometimes R is used when there is no confusion between transformations and the set of real numbers. The capital letter I still denotes the identity transformation. It carries each element onto itself.
[4.2] The following are four transformations I,R,S,T defined on the set {a,b,c,d} of four distinct elements:
[4.3] The following are four (new) transformations I,R,S,T defined on the set J = {...-2, -1, 0, 1, 2, ...} of all integers:
It will be convenient soon to use a slightly different notation of a function carrying elements onto elements when that function is a transformation. The name of a transformation in this section and in the next section will be written after the name of the element. For example, (x)I = x, (x)R = x2, (x)S = x3, (x)T = 2x are the functions just given. As expected, (3)I = 3, (4)R = 16, (5)S = 125, (6)T = 64. People who work in advanced fields of algebra often prefer this notation. But people who work in analysis, like calculus, prefer the traditional notation f(x).
 [4.4]
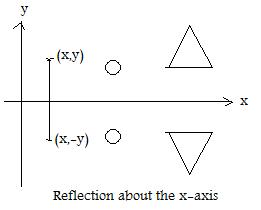
Many important transformations on the coordinate plane have a geometric character. The transformation F: coordinate plane --> coordinate plane defined by (x,y)F = (x,-y) carries points above the x-axis onto points below the x-axis. At the same time, F carries points below to points above. A circle above the x-axis is carried onto a congruent circle below. Similarly for line segments, triangles, parallelograms,...etc. In fact, everything below the x-axis is a mirror image of what is above the x-axis. (F is called a reflection of the plane about a line.)
[4.4]
Many important transformations on the coordinate plane have a geometric character. The transformation F: coordinate plane --> coordinate plane defined by (x,y)F = (x,-y) carries points above the x-axis onto points below the x-axis. At the same time, F carries points below to points above. A circle above the x-axis is carried onto a congruent circle below. Similarly for line segments, triangles, parallelograms,...etc. In fact, everything below the x-axis is a mirror image of what is above the x-axis. (F is called a reflection of the plane about a line.)
Because transformations are also functions, products of them can be made. In fact, there is no problem about not being conformable. Because there is only one set involved, the range of any transformation is contained in the domain of any transformation on that same set. In each of the above example all sorts of products can be formed: RS, RT, TR, RST, etc. Notice (2)ST = (4)T = 16. Products of transformations act on any element from left to right (the way English is read). For (x)ST, S acts first on x, and then T acts on the element (x)S. This is an advantage of the notation (x)T over T(x).
Let S and T be transformations on this set {4,6,9} defined by:
It is obvious that TS and ST do different things to elements 0,1,2. This shows that products of transformations may be non-commutative. The order of the product may be important, which transformation is applied first. The operation of forming products of transformations may not be commutative. Click here for a discussion of the associative law.
A transformation may have exponents, similar to exponents on real numbers.
Now extend the law of adding exponents to negative exponents on non-singular transformations: TT-1 = T1T-1 = T1-1 = T° = I. This means that T-1 is the inverse of T. The notation T-1 is used to represent the inverse of T and not the notation 1/T. The quotient of two transformations S/T is ambiguous - does it mean T-1S or does it mean ST-1, which may be different?
The extensions of the law of exponents makes the products of transformations behave like the products of real numbers. But not to go to extremes. (TS)2 may not equal T2S2 because the commutative law for products of transformations does not allways work. (But does (TS)2 = S2T2 ?)
A transformation on a set may carry any element x onto any element in the set, including itself.
[4.5] If a transformation carries an element back onto itself then that element is called a fixed point of that transformation. The transformation leaves that point fixed.
In example [4.2] element d is a fix point of transformation R and c is a fix point of S and T. In that same example, each of the four elements is a fixed point of the identity transformation I.
In example [4.3] only the integers 0 and 1 are fixed points of R and S. The transformation T has no fixed points. Every integer is a fixed point of the identity transformation I.
In example [4.4] the reflection F leaves every point on the line (x-axis) fixed. All other points are "moved."
[4.6] If a transformation on a set leaves every element in the set fixed, then that transformation must be the identity transformation I.
If a product of two transformations on the same set equals the identity transformation I then the left member of the product "undoes" what the right member does. If a transformation T adds 3 to every integer, and a second transformation S subtracts 3 from every integer, then ST = I (and TS = I).
[4.7] If the product of two transformations equals the identity transformation, the the product of those two transformations in the reverse order also equals the identity transformation.
This means that if the product ST = I then TS = I. So if one product is shown to be the identity then it is not necessary to show that the other product is also the identity.
Click here for more discussion.
If the product xy=1 of real numbers x and y then each is equal to the inverse of the other: y = x-1 and x = y-1.
[4.8] If the product of two transformations on the same set is equal to the identity transformation, then each of those transformations is called the inverse (transformation) of the other.
If a transformation T carries an element x onto an element y then the inverse transformation S must carry y back onto x, because ST = I the identity transformation: x = I(x) = ST(x) = S(y). The red = sign shows where the hypothesis ST = I is used. Intuitively speaking, an inverse transformation, if it exists, "undoes" what a tranformation does.
This observation provides methods for finding inverse transformations, if they exist, in many situations. To find the inverse transformation for T on the set P3 defined by
It is easy to check that the triple product RRR=I; This means that R2 is the inverse of R ! Also easily checked is FF=I. Therefore, F is its own inverse.
[4.10] For a very interesting and instructive comparison of the actions of R and F on a J3 and rotations and reflections of an equilateral triangle in a plane click here.
[4.11] The inverse of the inverse of a (non-singular) transformation is that transformation itself.
Let T be a non-singular transformation. Then 4.11] states that the inverse of T-1 is T itself. Then T-1T = I by definition. It also means that T is the inverse of T-1.
[4.12] The inverse of a product of non-singular transformations on the same set is equal to the product of their inverses taken in the reverse order.
If S and T are non-singular transformations on the same set, then (ST)-1 = T-1S-1. The proof is by algebraic manipulation of S and T using the associative law repeatedly to show the product T-1S-1 and ST is the identity transformation I. See [4.9].
[4.13] A transformation is non-singular if and only if it is a one-to-one corrspondence. A singular transformation fails to be one-to-one or fails to be "onto" (or both).
For example, the transformation R in example [4.2] has no inverse, because reversing the arrows there produces c --> a c -->b, which is not allowed for any function. (no single element can be carried by a function onto two different elements). Notice that reversing the arrows does not produce something that is "onto"
Similarly, the transformation R in example [4.3] has no inverse. R carries both 3 and -3 onto 9, 3 --> 9, -3 --> 9. Reversing arrows would carry 9 onto two different numbers, 3 and -3, again not allowed for any function.
Leaving points (elements) fixed is an important idea in mathematics. In example [4.2] the transformations I,S,T all leave the element c fixed. Notice that the product ST leaves c fixed: ST(c) = S(c) = c. Similarly TS leaves c fixed.
[4.14] If two transformations on the same set leave some element fixed, then their products leave that same element fixed.
[4.15] If a non-singular transformation leaves an element fixed, then its inverse transformation also leaves that same element fixed.
This is obvious using the arrow notation to find the inverse. If w is left fixed by a transformation, then in arrow notation w --> w. Reversing the arrow shows the same thing, but this means that the inverse transformation also leaves w fixed.
It is possible that a transformation has more than one fixed point. The identity transformation is a trivial example. Let S and T be two transformations on P6 = {1,2,3,4,5,6} defined as follows:
[4.16]
A subset can be left fixed by a transformation in two ways:
(a)pointwise: it leaves every element in the subset fixed.
(b)setwise: it carries the subset back onto itself.
By the way [4.16] is stated, if a transformation leaves a subset fixed pointwise, it also leaves that subset fixed setwise. The converse is not true. But in either situation, the transformation acts as a one-to-one correspondence between the subset and itself.
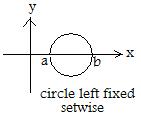
The adjacent figure shows another reflection of the plane about the horizontal x-axis, as was mentioned in [4.4]. The reflection carries the circle back onto itself because the horizontal line bisects the circle and its interior. However only the points a and b at the ends of the diameter along the horizontal line are left fixed pointwise by the reflection. This shows that a subset left fixed setwise may have some elements in it that are left fixed pointwise.
[4.17] If two transformations on the same set leave the same subset fixed setwise, then their product leaves that subset fixed setwise.
[4.18] If a non-singular transformation leaves a subset fixed setwise, then its inverse transformation also leaves that same subset fixed setwise.
Click here to see discussions of [4.13] and [4.14]
The transformation F in example [4.5] has the peculiar property that it is equal to its own inverse transformation: F-1 = F. The reflection of the plane about the x-axis in example [4.4] is another example.
[4.19] A non-singular transformation which is equal to its own inverse transformation is called an involution.
Any transformation is an involution if its square leaves every element fixed. Transformation T is an involution if T2 = I. Obviously the identity transformation I is an involution. On small sets, it is easy to construct involutions. If a --> b, where a,b are distinct elements, then some where in the listing have b --> a. Allow any other elements to be fixed. On the set J of integers, the transformation x --> -x is an involution, because a double negative is a positive, and zero is left fixed.
If an involution is done twice then that is equivalent to doing nothing. If the hands of a clock are moved ahead 6 hours twice, then the hands look like they were never moved. By [4.11] the process of taking inverses of (non-singular) transformations has the sense of being involuntary.