Section 5  Permutations

Now the balls are taken out, mixed up, and placed back into the five containers. The results are shown in Fig (A)T.

It is obvious that a rearrangement of the balls has happened in going from Fig A to Fig (A)T. Let T be the name of the rearrangement (mix up) process.

Start all over again. Start again with empty containers as in Fig E.

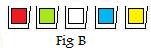Fig B shows colored blocks in all the containers.


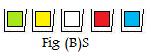They are removed, "mixed up", and placed back in the containers. The rearrangement is shown in Fig (B)S. Let S be the name of the rearrangement ("mix up") process.

[5.1] A physical permutation is a physical process for rearrangement of objects, usually by all the objects being picked up and put back.

In the two examples above T and S are names of the physical permutations. It can be said that the two physical permutations are the same:  T = S.

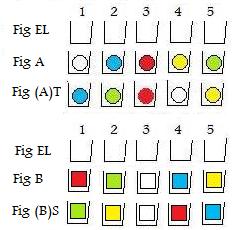
To support this statement, attach numbers to the containers. The most natural way to do this is to start counting the containers, going from left to right as shown in Fig EL. These labels provide identification for the containers. And they do much more. They reveal the "basic scheme" of the permutation.

What does the physical permutation do with the content of container 1? That content is moved to container 4. The content of container 2 is moved to container 1. The content of container 3 is left where it is, a sort of fixed point. The content of container 4 is moved to container 5. Finally, the content of container 5 is moved to container 2. This is true for figures A, (A)T and B,(B)S. Using arrows to mean "moved to", the basic schemes of the physical permutations for T and S are shown in the following:

Notice that distinct integers are carried onto distinct integers, and that every integer in P₅ is an image. The arrow notation above could be replaced by the two headed arrows that symbolize one-to-one correspondences.

[5.2a] A permutation on P_n is a one-to-one correspondence of P_n with itself.

A more general definition is the following:

[5.2b] A permutation is a non-singular transformation on a finite set.

In most of the discussions in this section, the physical permutation of n objects is "transferred" to a corresponding permutation of the integers in P_n = {1,2,...,n}. This is done by giving the places (containers) of each object a label of an integer in P_n

The arrow notation of a permutation often requires many lines of space to list everything. A shorter notation uses three rows to include the name:

The array notation is very brief and is also a convenient form for data stored on paper or in a computer file. By supplying positive integers in their natural order, the array '6 4 1 3 2 5' is easily converted into the two row notation:

In a motel with six rooms, there is one guest in each room. The manager of the motel decides to rearrange the people in the rooms. He could have everybody assemble in the hall and tell them where to go, according to the above permutation. Instead he decides to move each person one at a time. He tells the person in room 1 to go to room 6 which the guest does. The manager goes with the guest. 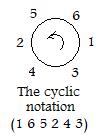At room 6, the manager tells the occupant there to go to room 5, etc. This process can be described by a chain of arrows notation:

The arrows in this chain could be erased and the numbers placed counterclockwise around a circle as shown in the adjacent figure. In a horizontal notation the permutation is written as (1 6 5 2 4 3 ). The number one is written only once. It is understood that the 1 also follows the 3 at the end. For obvious reasons this is called the cyclic notation for the permutation. and the numbers form a cycle. The cycle can begin with any number: (5 2 4 3 1 6) = (4 3 1 6 5 2) = (1 6 5 2 4 3).

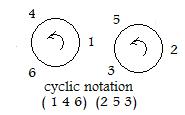The permutation '4 5 2 6 3 1' requires two circles as shown. Starting with 1, the following chain of arrows is produced:

The permutation

Sometimes the number of all permutations is needed. More exactly, how many ways may n objects be arranged in a row? The problem is equivalent to asking how many permutations of the array '1 2 ... n' are there. Experimenting:
n=1    '1'
n=2    '1 2',  '2 1'
n=3    '1 2 3',  '1 3 2',  '2 1 3',  '2 3 1',  '3 1 2',  '3 2 1'
n=4     ... (there are 24 permutations)
n=5     ... (there are 120 permutations)
n=6     ... (there are 720 permutations)
Make a table:
      1      1
      2      2
      3      6
      4      24
      5      120
      6      720
A common symbol for the number of permutations on {1,2,3,...,n} is n!. So,

[5.3] The number of permutations of n distinct objects is n! = 1x2x3x...xn.

n! is called n factorial. For a more detetailed discussion of factorials and the number of permutations click here.

The product of transformations has already been discussed in the previous section 4. Since permutations are also transformations their products have already been defined. Click here for more about products of permutations and of permutations written as cycles. Also the inverse of a transformation has been already discussed. But click here for more about inverses of permutations and of permutations written as cycles.

Between the collection of all permutations on P₃ and the physical movements of an equilateral triangle there is an interesting correspondence. If the opening example of balls placed in cans, to start we could put a ball into a container labeled 1, a ball into a container labeled 2, and a ball into a container labeled 3. Suppose the containers are placed the same distance apart, and a rigid triangular iron frame is attached firmly to the containers. See figure Fig A just below the adjacent figure AF. Instead of balls going into the containers, place an colored equilateral triangle inside this iron frame so that the red angle points to 1, the green angle points to 2, and the remaining blue angle points to 3.

A physical permutation will occur when the triangle is picked up, "mixed up", and placed back in the iron frame. (The shape of the triangle must not be distorted or changed in the process. Hence the movments are called rigid motions.)

The center of the colored triangle is tht point where the three colors meet. It is always in the same place before and after that triangle has been picked up and placed back. Suppose the triangle in Fig A is picked up, rotated +120° counter-clockwise and put back inside the iron frame, as shown in Fig B. A rotation R has taken place. R = '2 3 1'.

Now, instead of a rotation, suppose the colored triangle in Fig A is picked up, flipped about an altitude from 3, and placed back in the iron frame, as shown in Fig AF. A reflection F has occurred where the red angle and green angle have been interchanged. F = '2 1 3'.

For a discussion in more detail click on The Six Symmetries of an Equilateral Triangle. In that discussion the following "symmetries were developed:
                                                                  I,R,R²,F,FR,RF
and the followowing equations relating these "symmetries":
[5.4]                                                    R³=I, F²=I, FR=R²F, RF=FR²